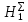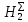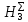Иллюстрация уравнения Бернулли. Построение диаграммы напоров. Изучение закона сохранения энергии по визуально наблюдаемой пьезом. Отчет по лабораторной работе 5 Тема Иллюстрация уравнения Бернулли. Построение диаграммы напоров. Изучение закона сохранения энергии по визуально наблюдаемой пьезометрической линии при сужении трубопровода и расширении
 Скачать 0.5 Mb. Скачать 0.5 Mb.
|
|
Первое высшее техническое учебное заведение России  Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования Санкт-Петербургский горный университет Кафедра транспорта и хранения нефти и газа Отчет по лабораторной работе №5 Тема: «Иллюстрация уравнения Бернулли. Построение диаграммы напоров. Изучение закона сохранения энергии по визуально наблюдаемой пьезометрической линии при сужении трубопровода и расширении» Выполнили: студент гр.НБ-19 _________ /Шатохин А.С./ (подпись) (Ф.И.О.) Проверил: ассистент _________ /Касьянов А.В./ (подпись) (Ф.И.О.) Санкт-Петербург 2021 I. Цель работы Изучение закономерностей течения жидкости (уравнения Бернулли) в сложном трубопроводе при последовательном соединении участков разного диаметра. Экспериментальное построение напорной характеристики, построение напорной и пьезометрической линий сложного трубопровода. Изучение влияния геометрической высоты трубопровода на величины полного и гидростатического напора и расход через трубопровод. II. Теоретические основы работы На практике достаточно часто встречаются «сложные» трубопроводы, состоящие из участков различного диаметра, соединительных деталей и т.д. Исследовать гидравлические режимы таких систем можно с использованием диаграммы напоров. Особую важность графическое построение напорной линии приобретает для протяженных линейных трубопроводов – водоводов, нефтепроводов и т.д. Уравнение Бернулли в общем виде записывается следующим образом: 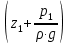 + +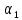 ∙ ∙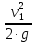 = =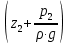 + +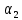 ∙ ∙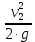 +Δ +Δ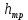 , (1) , (1)где 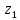 – геодезический напор в сечении 1; – геодезический напор в сечении 1;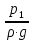 – пьезометрический напор в сечении 1 (удельная потенциальная энергия давления); – пьезометрический напор в сечении 1 (удельная потенциальная энергия давления); 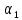 ∙ ∙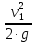 – скоростной напор в сечении 1 (удельная кинетическая энергия ); Δ – скоростной напор в сечении 1 (удельная кинетическая энергия ); Δ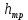 – потери напора на трение между сечениями. Для сечения 2 обозначения аналогичны. – потери напора на трение между сечениями. Для сечения 2 обозначения аналогичны. Уравнение Бернулли является одной из форм закона сохранения энергии. Исходя из него, очевидно, что линия полного напора может только падать вдоль трубопровода, не имеющего дополнительных подкачек, поскольку энергия потока безвозвратно расходуется на трение. Линия же пьезометрических напоров может как падать, так и расти. Линию пьезометрических напоров строят по показаниям пьезометров. Дополнив в каждой точке линию пьезометрических напоров на величину скоростных напоров – получают линию полного напора. Все построения осуществляются при фиксированном расходе. Средняя скорость жидкости: 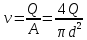 (2) (2)Критерий Рейнольдса: 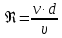 (3) (3)Скоростной напор: 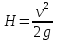 (4) (4)Потребные пьезометрические напоры для каждого участка: 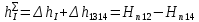 (5) (5)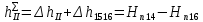 (6) (6)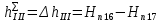 (7) (7)Потребный пьезометрический напор сложного трубопровода: 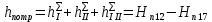 (8) (8)Потребные полные напоры участка и трубопровода в целом: 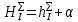 ∙ ∙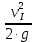 (9) (9)Полный напор сложного трубопровода с последовательным соединением: 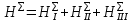 (10) (10)Полный напор в сечении: 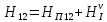 (11) (11)Зависимость потерь полного напора в местных сопротивлениях от числа Рейнольдса: А) для плавного сужения Δ 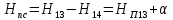 ∙ ∙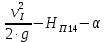 ∙ ∙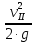 (12) (12)Б) для плавного расширения Δ 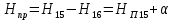 ∙ ∙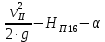 ∙ ∙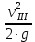 (13) (13)Величины коэффициентов сопротивлений плавного сужения и внезапного расширения: 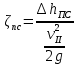 (14) (14)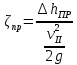 (15) (15)Работа выполнялась на учебном стенде «Основы механики жидкости» (ОМЖ-016-10ЛР-01) (рисунки 1-2). 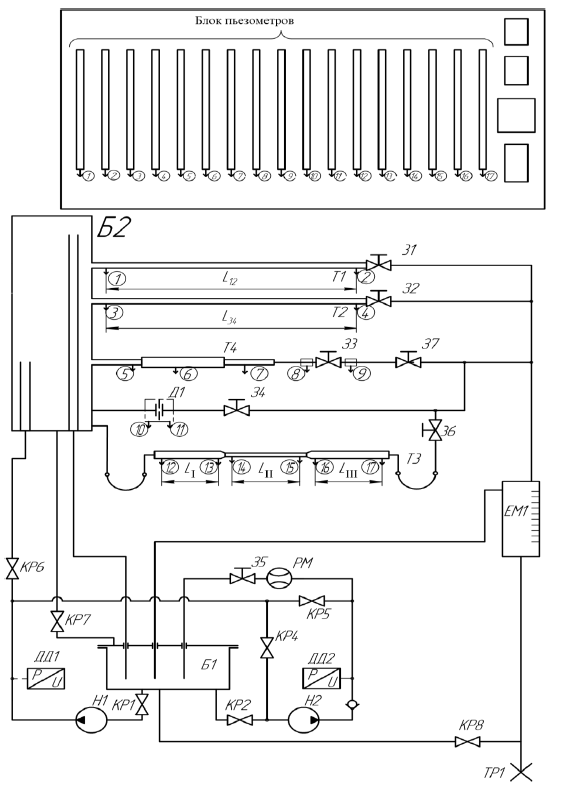 Рисунок 1 – Схема учебного стенда «Основы механики жидкости» (ОМЖ-016-10ЛР-01)  Рисунок 2 - Типовой комплект учебного оборудования ОМЖ-016-10ЛР-01. Общий вид. Таблица 1. Состав учебного стенда «Основы механики жидкости»
III. Ход работы Порядок выполнения работы и формулы для вычислений Сложный трубопровод состоит из трех последовательно соединенных прозрачных труб из органического стекла с внутренними диаметрами dI =15 мм, dII =10 мм, dIII =15мм. Расстояния между точками отбора и схему подключения пьезометров см. рисунок 1. Для исследования влияния изменений геометрического напора конструкцией стенда предусмотрена возможность изменения угла наклона оси трубопровода к горизонту. Переходы между участками трубопровода выполнены в виде конусов (конфузора и диффузора). Примеры вычислений для опыта 1 Средняя скорость жидкости (формула 2):  1,07 м/c 1,07 м/cКритерий Рейнольдса (формула 3): 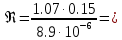 1799,5 1799,5 Скоростной напор (формула 4): 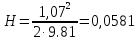 м мПотребные пьезометрические напоры для каждого участка (формулы 5, 6, 7): 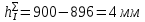 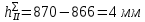 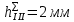 Потребный пьезометрический напор сложного трубопровода (формула 8): 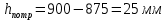 (8) (8)Потребные полные напоры участка и трубопровода в целом (формула 9): 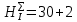 ∙ ∙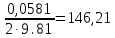 мм ммПолный напор сложного трубопровода с последовательным соединением (формула 10): 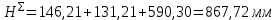 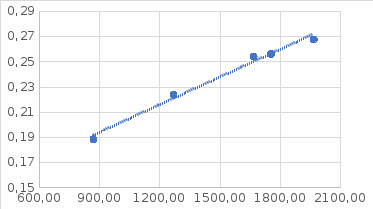 Рисунок 3 – График зависимости полного напора сложного трубопровода от расхода жидкости Полный напор в сечении (формула 11): 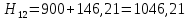 мм ммЗависимость потерь полного напора в местных сопротивлениях от числа Рейнольдса, графики которых представлены на рисунках 4 и 5: А) для плавного сужения (формула 12) Δ 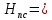 1042,21-1042,21=41 мм 1042,21-1042,21=41 ммБ) для плавного расширения (формула 13) Δ 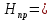 997,21 997,21 1467,30 1467,30 -470,09 мм -470,09 мм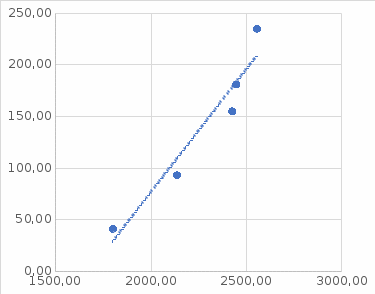 Рисунок 4 – График зависимости напора для плавного сужения от числа Рейнольдса (Re) 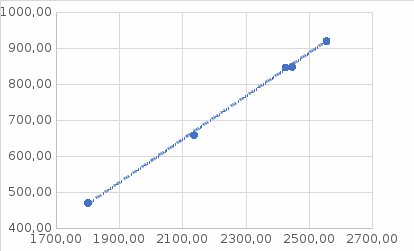 Рисунок 5 – График зависимости напора для плавного расширения от числа Рейнольдса (Re) Величины коэффициентов сопротивлений плавного сужения и внезапного расширения (формулы 14 и 15), графики которых представлены на рисунках 6 и 7: 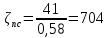 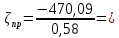 -8082 -8082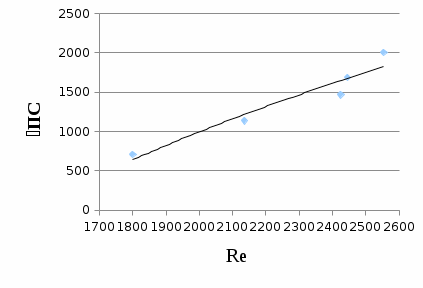 Рисунок 6 – График зависимости коэффициента сопротивления плавного сужения от числа Рейнольдса (Re) 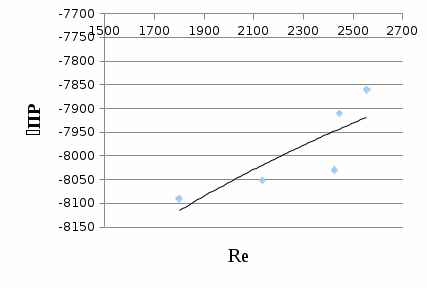 Рисунок 7 – График зависимости коэффициента сопротивления внезапного расширения от числа Рейнольдса (Re) Аналогичные расчеты проводятся для всех экспериментов №1-10 и результаты расчетов заносятся в таблицу 2 и на их основе строятся графики, представленные на рисунках 2-4. Таблица 1.1 – Экспериментальные данные
Продолжение таблицы 1.1
Таблица 2.1 – Экспериментальные данные
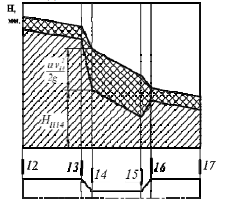 Рисунок 8 – Пьезометрическая и напорная линии IV. Вывод В ходе работы был построен график зависимости суммы полных напоров участков от расхода (рисунок 3). Из графика видно, что с увеличением расхода жидкости увеличивается и полный напор. Также построены графики зависимости потерь полного напора в местных сопротивлениях от числа Рейнольдса для плавного сужения и для плавного расширения – рисунки 4 и 5. Из рисунка 3 видно, что с увеличением числа Рейнольдса при плавном сужении увеличиваются потери напора в местных сопротивлениях. Из рисунка 5 видно, что при увеличении числа Рейнольдса увеличивается и потери напора при плавном расширении. Были построены графики зависимости коэффициентов сопротивлений плавного сужения и внезапного расширения от числа Рейнольдса – рисунки 6 и 7. Из рисунка 6 видно, что с увеличением числа Рейнольдса, коэффициент сопротивления плавного сужения уменьшается. Из рисунка 7 видно, что с увеличением числа Рейнольдса, коэффициент сопротивления резкого расширения увеличивается. |

 ,
, ,
, ,
,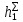 ,
,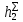 ,
,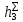 ,
,