Отчет по лабораторной работе 6 Выполнили студент ивт22 Иплаев А. Д., подпись дата
 Скачать 230.51 Kb. Скачать 230.51 Kb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное ГОСУДАРСТВЕННОЕ бюджетное ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «ПОВОЛЖСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ» Факультет информатики и вычислительной техники Кафедра информационно- вычислительных систем Сумматоры и АЛУ отчет по лабораторной работе №6 Выполнили: студент ИВТ-22 ________Иплаев А. Д. _________, подпись дата Проверил: к.т.н., доцент ________ Старыгин С.В. _________ подпись дата Оценка _____________ Йошкар-Ола 2013 г. Цель работы: знакомство с сумматорами и АЛУ.1. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ. 6.1.Сумматоры Сумматоры предназначены для выполнения операций сложения и вычитания как двоичных, так и десятичных чисел, а также используются для построения различных решающих цифровых устройств. Сумматор (двоичный) – комбинационная схема, выполняющая сложение двух двоичных чисел x и y. Сложение разрядов осуществляется по единым правилам, т.е. в каждом i-том разряде осуществляется сложение – xi и yi и Ci-1 – перенос от сложения предыдущих разрядов. Результат сложения представлен суммой Si и переносом Сi в старший i+1 разряд. Сумматоры подразделяются на полусумматоры, имеющие два входа (отсутствует вход переноса), полные сумматоры, имеющие три входа. Полусумматоры описываются следующими функциями: 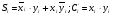 . .Полные сумматоры описываются выражениями следующего вида: 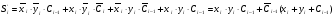 , ,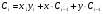 . . Используя аксиомы алгебры логики, можно по-разному преобразовать приведенные выражения, исходя из базиса используемых ИМС. Для указанных выражений наиболее удобны логические ИМС типа ЛР, которые оптимальным образом позволяют реализовать функции для S и С (рис. 65,а). 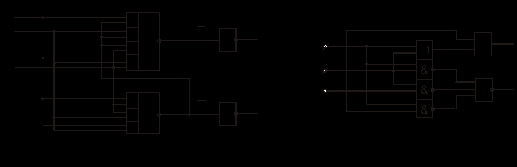 Рис. 65 После преобразования приведенных выражений можно получить: 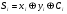 ; ; 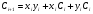 . .Исходя из этих выражений, схема полного сумматора примет вид, изображенный на рис. 65,б. В данной схеме удобно использовать ЛЭ ‘’Исключающее ИЛИ’’. Схема полусумматора может быть реализована на двух логических элементах (рис. 66,а), а используя две схемы полусумматоров, можно реализовать полный сумматор (рис. 66,б). УГО сумматора представлено на рис. 66,в. 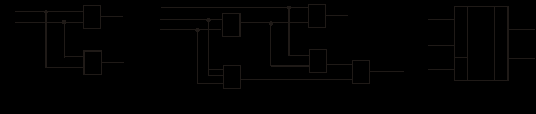 Рис. 66 6.2. Применение сумматоровВ виде отдельных ИМС выпускаются одно-, двух- и четырехразрядные сумматоры. В качестве примера на рис. 67 приведены:
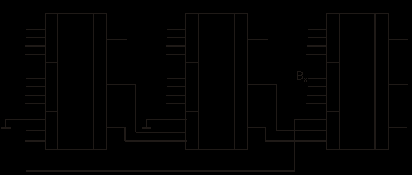
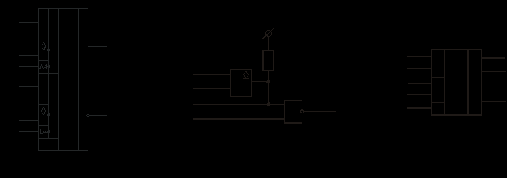 Рис. 67 ИМ5 – два одноразрядных сумматора, ИМ3 – 4-х разрядный сумматор (два ИМ2 – с последовательным формированием переноса). В многоразрядных схемах сумматоры соединяются последовательно. Такие схемы называются сумматоры с последовательным переносом (рис. 68). 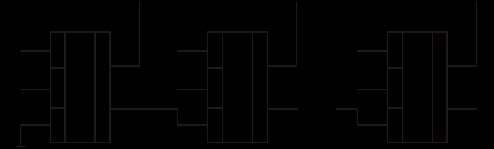 Рис. 68 Основным параметром параллельного сумматора с последовательным переносом является быстродействие – время формирования n-разрядного кода суммы. Т.к. перенос в сумматоре формируется последовательно при поразрядном сложении, то время формирования суммы будет определяться количеством разрядов сумматора. Для n-разрядного сумматора время сложения определяется ts=ntзд.р., где tзд.р. – время формирования суммы одного разряда. Для увеличения быстродействия многоразрядных сумматоров необходимо уменьшить время распространения сигнала переноса от входа C0 до входа Cn. Для этой цели используются комбинационные схемы, которые называются схемами переноса или схемами ускоренного переноса (Carry Unit - устройство переноса). ИМС ИМ6 – представляет собой 4-разрядный сумматор со схемой ускоренного переноса (CRU). Функциональная схема ИМ6 представлена на рис. 69. 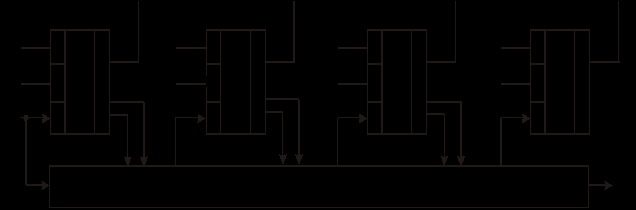 Рис. 69 Функциональная схема одного разряда сумматора представлена на рис. 70. Сигналы gi и Pi используются в схеме CRU для ускоренного формирования переносов. 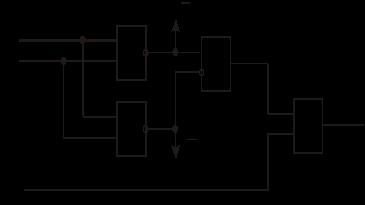 Рис. 70 При сложении двоичных чисел в обратных кодах возникает так называемый циклический перенос. Для устранения данного эффекта используется дополнительный код. Для преобразования обратного кода в дополнительный и наоборот используют схемы сумматоров с дополнительной логикой (рис. 71).ц 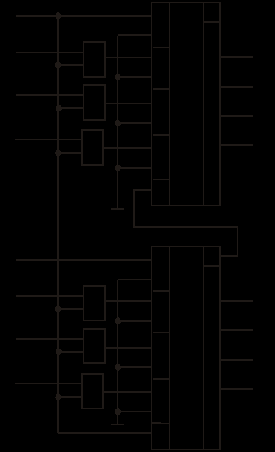 Рис. 71 Старший разряд входного числа х7 является знаковым. На вход сумматора поступает прямой код числа Х 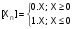 . При положительном входном числе Х, когда х7 = 0, ai = 0 Е Хi = Хi и Si = Хi, т.е. код числа не меняется, т.к. число положительное. Если же х7 = 1 (Х - отрицательное число), то ai = 1 Е Хi = Хi, и сумматор выполняет вычисления: . При положительном входном числе Х, когда х7 = 0, ai = 0 Е Хi = Хi и Si = Хi, т.е. код числа не меняется, т.к. число положительное. Если же х7 = 1 (Х - отрицательное число), то ai = 1 Е Хi = Хi, и сумматор выполняет вычисления: 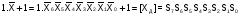 . В результате в младший перенос при отрицательном числе поступает 1 и на выходе формируется дополнительный код. . В результате в младший перенос при отрицательном числе поступает 1 и на выходе формируется дополнительный код.При использовании данной схемы для обратного преобразования необходимо выполнение условия [ХП] Ј 27 1 = 127; [ХД] №1.0000000, т.к. старший разряд х7 является знаковым. На рис. 72 представлена схема сумматора-вычитателя, который выполняет вычисления по выражению: 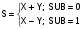 , где X и Y – 7-разрядные числа (Х – положительное без знака, знаковый разряд числа Y y7 определяет знак операции SUB). , где X и Y – 7-разрядные числа (Х – положительное без знака, знаковый разряд числа Y y7 определяет знак операции SUB). Если SUB =1, то код числа Y преобразуется в дополнительный и выполняется операция 0.Х+1. 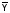 +1 = [SД]; при SUB = 0 происходит сложение прямых кодов входных чисел Х иY 0.X + 0.Y = [SП]. SД - дополнительный код суммы, SП - прямой код суммы. +1 = [SД]; при SUB = 0 происходит сложение прямых кодов входных чисел Х иY 0.X + 0.Y = [SП]. SД - дополнительный код суммы, SП - прямой код суммы. |
| | | | | 23 | 22 | 21 | 20 | | |
| | | | | 1 | 1 | 0 | 1 | | X |
| | | | | 1 | 0 | 1 | 1 | | Y |
| | | | | 1 | 1 | 0 | 1 | | P0 |
| | | | 1 | 1 | 0 | 1 | | | P1 |
| | | 0 | 0 | 0 | 0 | | | | P2 |
| | 1 | 1 | 0 | 1 | | | | | P3 |
| 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | | P |
| 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 | | |
где X – n-разрядное множимое,
Y – m-разрядный множитель,
Pj=Xyj2j – частные произведения.
В качестве примера приведен процесс умножения двух чисел с разрядностью n = m = 4.
На рис. 83 приведена схема 4-х разрядного умножителя, реализованного по приведенному алгоритму с использованием ИМС полных сумматоров.
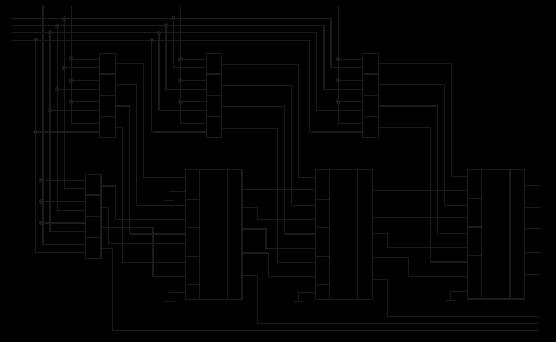
Рис. 83
13.1. Матричные умножители
Алгоритм матричного умножения можно записать в виде: XnґYm+An+Bm, где An и Bm – дополнения из младших разрядов при умножении. Максимальная разрядность результата умножения определяется выражением 2n+m -1 и определяется суммой разрядностей операндов.
Для 2-х разрядных чисел n = m = 2 можно записать алгоритм умножения в виде:
X2×Y2+A2+B2 = x1x0 ґy1y0+a1a0+b1b0 = x1y122 + (x1y0+x0y1+a1+b1)21 + (x0y0+a0+b0)20.
Такое вычисление можно реализовать с помощью четырех одноразрядных сумматоров типа ИМ1 (рис. 84).
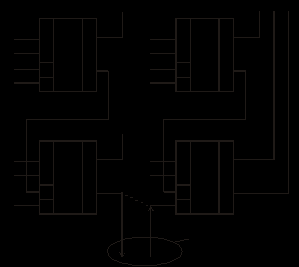
Рис. 84
Операция умножения xi yi осуществляется логическими элементами «И», которые являются входными блоками сумматоров ИМ1. Сумма и перенос определяется выражениями:

Графически формирование произведения можно представить в виде:
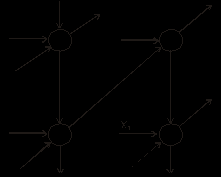
Такая схема имеет регулярную структуру и может быть расширена до любых значений. Комбинационные схемы, имеющие такую функцию, называются матричными умножителями.
По данной схеме выполнена ИМС ИП5 – матричный умножитель 2ґ2. Условное обозначение MPL (Multiplier - умножитель) (рис. 85,а). Одноразрядные сумматоры в ИМС ИП5 реализованы по схеме на рис. 85,б.
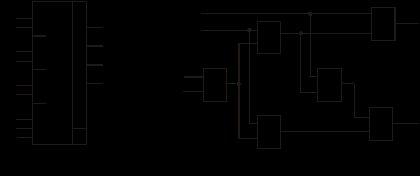
Рис. 85
Существуют быстрые матричные умножители, использующие ускоренный алгоритм вычисления частичных произведений. Например: ИП8, ИК1 – быстрые умножители 4ґ2.
1802ВР4 – специализированная БИС умножения 12ґ12; tумн»100нсек, Pпот= 3Вт. Функциональная схема 1802ВР4 предсталвена на рис. 86.
Сигналы TCY, TCX указывают на дополнительный код умножаемых чисел.
CL и CM – (L – Least - младший, M – Most - старший) – тактовые сигналы записи младшей и старшей групп произведения.
SU – сдвигающее устройство.
Сигнал
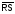 (Right Shift – сдвиг вправо) указывает на присвоение знака произведения младшей группе.
(Right Shift – сдвиг вправо) указывает на присвоение знака произведения младшей группе.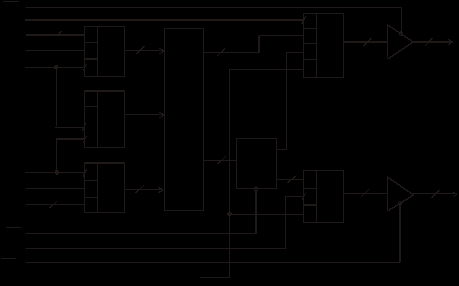
Рис. 86.
FT – сигнал «прозрачности» регистров произведения.
По аналогичной структуре реализованы матричные умножители типа 1802ВР3 – 8х8 и 1802ВР5 – 16х16.
В настоящее время максимальную производительность обеспечивают умножители, реализованные на ПЗУ.
3.2. Последовательные умножители
В последовательных умножителях множимое Xn записывается в регистр, а разряды множителя Ym поступают последовательно, начиная с младшего разряда. В результате последовательно формулируются частичные произведения и происходит их арифметическое накопление. На рис. 87 приведена схема последовательного умножителя ИП9 – умножитель 8х1. Сигнал М определяет режим работы, При М = 0 происходит загрузка числа Х, при М =1 выполняется операция сдвига и поразрядное умножение. Множитель Y может имеет произвольную разрядность.
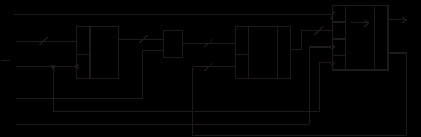
Рис. 87
2. ПРАКТИЧЕСКАЯ ЧАСТЬ
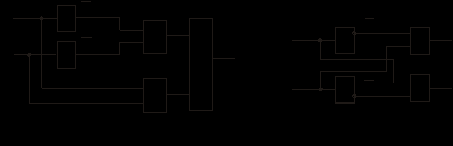
Задание: Разработать схему сумматора трех двухразрядных чисел (А+В+С).
Схема:
a0
SM
ci-1
a
b
ci
S
0
b0
Cвх
a1
SM
ci-1
a
b
ci
S
1
b1
Cвых
SM
ci-1
a
b
ci
S
2
SM
ci-1
a
b
ci
S
3
c0
c1
SM
ci-1
a
b
ci
S
0
S0
S1
S2

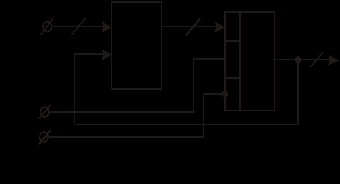
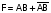 . На рис. 76,а представлена функциональная схема реализующая функцию
. На рис. 76,а представлена функциональная схема реализующая функцию  .
. 
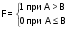 ;
; 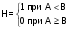 .
.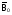 ,
, 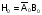 (рис. 76,б).
(рис. 76,б).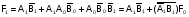


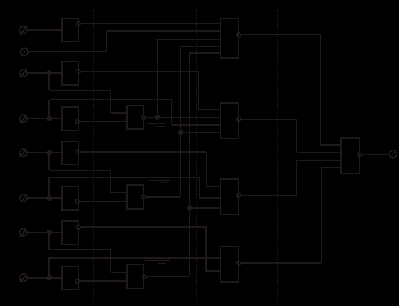

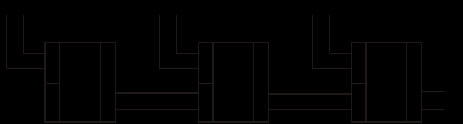

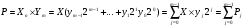 ,
,