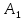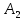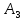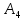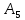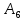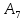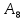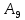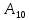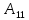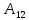Отчет по лабораторной работе 8
 Скачать 271.82 Kb. Скачать 271.82 Kb.
|
|
Отчет по лабораторной работе 8. Анализ и организация производства методами сетевого планирования. Постановка задачи с учетом значений p и q. ( p=1, q=8) Машиностроительный завод планирует наладить производство новых станков с числовым программным управлением (ЧПУ) для изготовления деталей. При подготовке технического задания на проект был составлен перечень необходимых для его реализации работ и с учетом существующих норм времени их выполнения сделана оценка продолжительности каждой работы (табл. 8.1).
Двойное обозначение в виде латинской буквы (А, В, С, …) и переменных с индексами (А1, А2, …) в табл. 8.1 используется в целях дальнейшего удобства изложения материала. Порядок следования перечисленных в табл. 8.1 работ при выполнении проекта приведен в табл. 8.2.  С учетом имеющегося перечня работ проекта (табл. 8.1) необходимо: 1. Определить критический путь. 2. Найти минимальное время, которое потребуется на выполнение всего проекта. 3. Найти допустимые сроки смешения выполнения отдельных работ без увеличения общего срока реализации проекта. 4. Построить линейный график выполнения работ (диаграмму Ганта). Формулы для расчета ранних и поздних сроков свершения событий и рассчитать их. Используя табл. 8.3, перейдем к решению поставленных в лабораторной работе задач. Для этого сформируем в Excel таблицу, включающую исходные данные: матрицу инциденций и продолжительность выполняемых работ. При этом для фиктивных работ длительность принимается равной 0 (рис. 8.3). 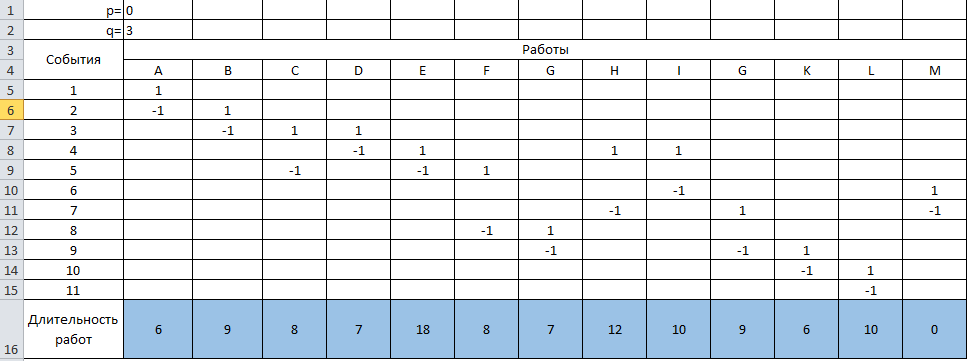 Для критического пути определим ранние и поздние сроки наступления событий, используя определяющие их соотношения. Ранний срок наступления события j вычисляется по формуле: где 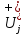 – множество работ, входящих в вершину, соответствующую событию j на сети; t i p – ранний срок выполнения начального события работы i, j; Поздний срок наступления события i находят по формуле: – множество работ, входящих в вершину, соответствующую событию j на сети; t i p – ранний срок выполнения начального события работы i, j; Поздний срок наступления события i находят по формуле:где 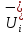 – множество работ, выходящих из события i на сети; – множество работ, выходящих из события i на сети; 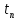 j – поздний срок свершения конечного события j работы i, j. Рассчитаем ранние сроки наступления событий. Для этого сформируем матрицу, одновременно характеризующую порядок следования и продолжительности работ, как показано на рис. 8.4. В этой матрице на пересечении i-й и j-й строк, соответствующих событиям i и j (вершины графа), задает продолжительность работы i, j. Если работа, связанная с событиями i и j, не выполнялась по проекту, то соответствующая ячейка остается не заполненной. В этой же таблице предусмотрим столбец, который будем использовать для последующего вычисления ранних сроков событий ( j – поздний срок свершения конечного события j работы i, j. Рассчитаем ранние сроки наступления событий. Для этого сформируем матрицу, одновременно характеризующую порядок следования и продолжительности работ, как показано на рис. 8.4. В этой матрице на пересечении i-й и j-й строк, соответствующих событиям i и j (вершины графа), задает продолжительность работы i, j. Если работа, связанная с событиями i и j, не выполнялась по проекту, то соответствующая ячейка остается не заполненной. В этой же таблице предусмотрим столбец, который будем использовать для последующего вычисления ранних сроков событий (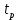 ). ).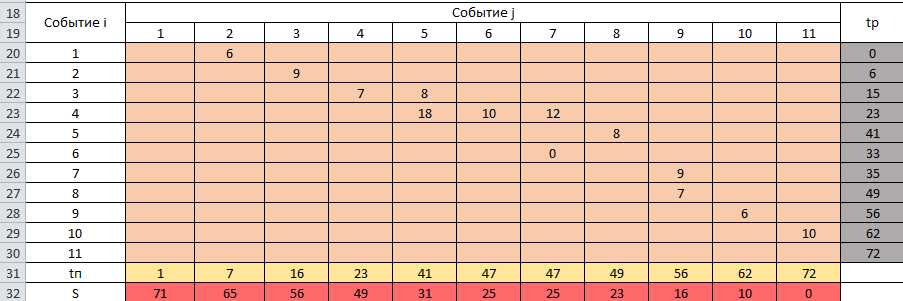 Ранний срок свершения события 1 равен 0, поэтому в ячейку М20 записываем 0. Остальные значения ранних сроков свершения событий рассчитаем согласно формуле (8.1). Так, ранний срок для события 2 вычисляется следующим образом. Просматривается столбец, соответствующий событию 2 (j=2). Имеющиеся там значения продолжительности работ складываются со значениями, найденными ранее в столбе 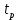 . Далее, среди полученных значений выбирается наибольшее. Выполняя указанные действия, в ячейку М21 записываем: . Далее, среди полученных значений выбирается наибольшее. Выполняя указанные действия, в ячейку М21 записываем:М21=C20+M20 Далее, в ячейки М22 и М23 записываем: М22=D21+M21 М23=E22+M22 Для ячейки М24 ранний срок находится так: двигаемся по столбцу j=5 и столбцу 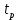 , рассматривая строки, в которых есть значения: , рассматривая строки, в которых есть значения:М24=МАКС(F22+M22;F23+M23) Остальные значения, расположенные в столбце, в который заносятся ранние сроки, находятся аналогично: М25=G23+M23 М26=МАКС(H23+M23;H25+M25)М27 28+5=33; M27=I24+M24 М28=МАКС(J26+M26;J27+M27) М29=K28+M28 М30=L29+M29 Согласно данным в таблице на рис. 8.4, получаем, что минимальное время завершения всех работ (критический срок) данного проекта равен 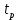 (11) (11) 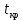 64 64Для вычисления поздних сроков добавим в таблицу на рис. 8.4 строки п t и s. Учитывая формулу (8.2) нахождения позднего срока свершения события j, получаем, что в строке s должно быть указано время, которое требуется для завершения работ, начинающихся после события j. Оно определяется следующим образом (рис. 8.4). Двигаемся по таблице от ячейки L32 к ячейке B32. В ячейку L32 записываем значение 0. Для определения значения в ячейке события j складываем значения в строке, соответствующей событию i j , с уже найденными значениями в строке s и выбираем наибольшее: K32 =L29+L32 J32=K28+K32, I32 =J26+J32, H32 =K28+K32 G32 =H25+H32, F32 =I24+I32, E32 =МАКС(F23+F32; G23+G32; H23+H32) D32 =МАКС(E22+E32;F22+F32) C32 =D21+D32 B32 =C20+C32 Поздний срок события j находится по формуле j 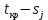 , то есть так: В31 =$М$30-В32. , то есть так: В31 =$М$30-В32.Описанный алгоритм определения поздних сроков последовательно применяется для всех событий сетевого графика (рис. 8.1) Формулу для расчета резерва времени для каждого события. Найдем критический путь. Критический путь характеризуется тем, что резервы времени событий, расположенных на нем пути равны нулю. Резервы времени для каждого из событий по формуле: Ri) 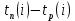 . (8.3) . (8.3) При этом ранние сроки копируем из предыдущей таблицы (рис. 8.4): R18 =M20. Для задания поздних сроков событий, транспонируем диапазон А31:L31. Для этого выполняем действия: – в ячейку записываем формулу S17 =ТРАНСП(А31:L31); – выделяем диапазон, где будет размещаться результат S17:S28, устанавливаем курсор в строку формул и нажимаем клавиши Ctrl, Shift и Enter. Учитывая равенство (8.3), введем формулу: T18 =S18-R18, которую распространяем на диапазон Т18:Т28. Сводим в таблицу ранние и поздние сроки всех событий (рис. 8.5). 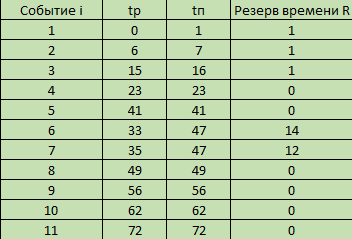 Сетевой график с указанием на нем критического пути. 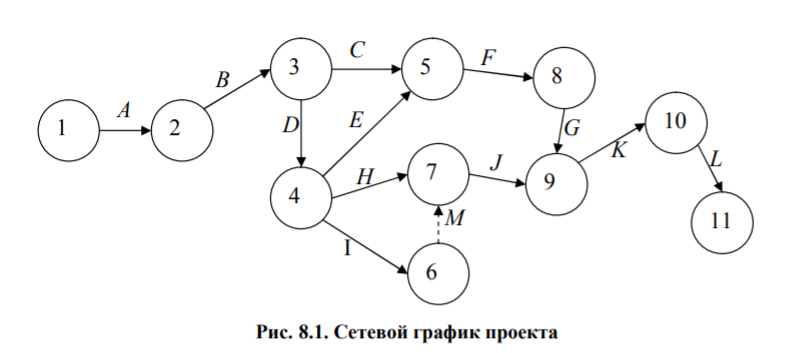 Формулы для расчета всех характеристик работ по проекту. При этом ранние сроки копируем из предыдущей таблицы (рис. 8.4): R18=M20. Для задания поздних сроков событий, транспонируем диапазон А31:L31. Для этого выполняем действия: – в ячейку записываем формулу S17=ТРАНСП(А31:L31); – выделяем диапазон, где будет размещаться результат S17:S28, устанавливаем курсор в строку формул и нажимаем клавиши Ctrl, Shift и Enter. Учитывая равенство (8.3), введем формулу: T18=S18-R18, которую распространяем на диапазон Т18:Т28. Учитывая данные, полученные в таблице на рис. 8.5, получаем, что на критическом пути лежат события 1-2-3-4-5-8-9-10-11. Соответствующие им работы 1-2 (А), 2-3 (В), 3-4 (D), 4-5 (E), 5-8 (F), 8-9 (G), 9-10 (K), 10-11 (L) являются критическими. Работы 3-5 (С), 4-7 (Н), 4-6 (I) и 7-9 (J) являются некритическими. Их сроки начала и окончания можно изменять, определив ранние и поздние сроки начала и окончания работ. Найдем ранние и поздние сроки начала и окончания работ. Для этого воспользуемся следующими формулами: 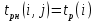 – ранний срок начала работы (i, j); – ранний срок начала работы (i, j);2) 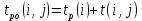 – ранний срок окончания работы (i, j); – ранний срок окончания работы (i, j);3) 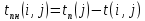 – поздний срок начала работы (i, j); – поздний срок начала работы (i, j);4) 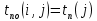 – поздний срок окончания работы (i, j). – поздний срок окончания работы (i, j).Используя матрицу инциденций (рис. 8.3), построим таблицу, указав в ней работы (рис. 8.6). Далее, в ячейку А35 вводим формулу: А35= =ТРАНСП(B4:N4), выделяем диапазон А35:А47, размещаем курсор в строке формул, нажимает кнопки Ctrl, Shift и Enter. Тогда, просматриваем матрицу инциденций, для каждой работы указываем соответствующие ей события. 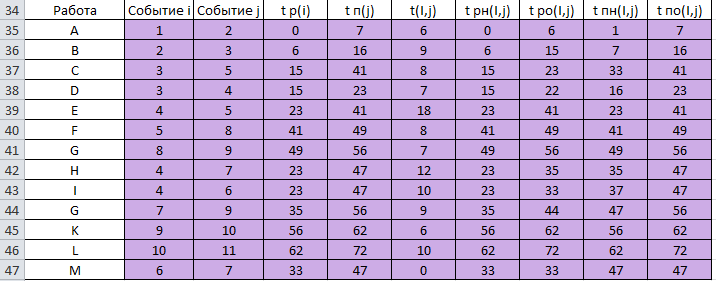 Для каждого события i задаем ранний срок его свершения, а для каждого события j - поздний срок, используя результаты выполненных ранее расчетов: 1) в диапазон D35:D47 заносим значения поздних сроков, соответствующих события i; 2) в диапазон Е35:Е47 заносим значения поздних сроков, соответствующих события j. В ячейки F35:F47 вносим продолжительность выполнения работ. Получить эти значения можно, транспонируя ячейки В16:N16, используя формулу F35=ТРАНСП(B16:N16). Для вычисления раннего срока начала работы (i, j)в столбце « 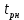 (i,j)» (i,j)»вводим формулу: G35=D35. Для вычисления позднего срока начала работы (i, j)в столбце « 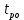 (i,j)» (i,j)»вводим формулу: Н35=D35+F35. Для вычисления позднего срока начала работы (i, j)в столбце « 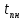 (i,j)» (i,j)»вводим формулу: I35=E35-F35. Для вычисления позднего срока начала работы (i, j)в столбце « 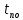 (i,j)» (i,j)»вводим формулу: J35=E35. Записанные формулы распространяем на вычисление всех величин, характеризующих работы сетевого графика, показанного на рис. 8.1. Линейный график работ (диаграмму Ганта) Построим линейный график выполнения работ. Для этого будем использовать линейчатые диаграммы. Выбираем вкладку «Вставка», раздел «Диаграммы» и тип диаграмм – линейчатая с накоплением. Добавим данные для построения – команда «Выбрать данные». В качестве подписей по горизонтальной оси выбираем наименование работ (диапазон А35:А47), а в область построения вносим данные из столбца – ранние сроки начала работы t i, j рн (диапазон G35:G47) (рис. 8.7). 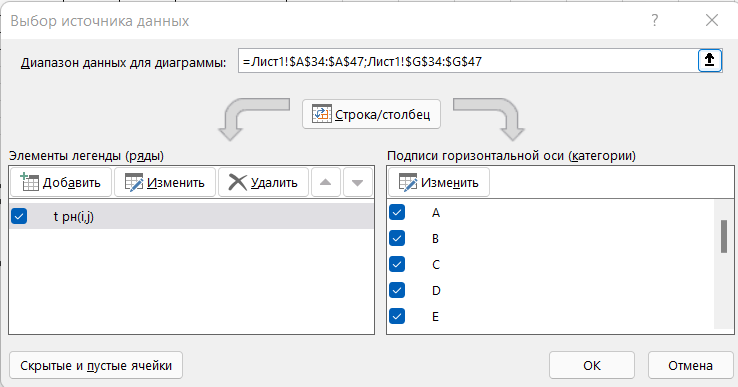 Добавим в область построения второй набор данных – продолжительности работ (диапазон F35:F47). В результате получаем график на рис. 8.8. 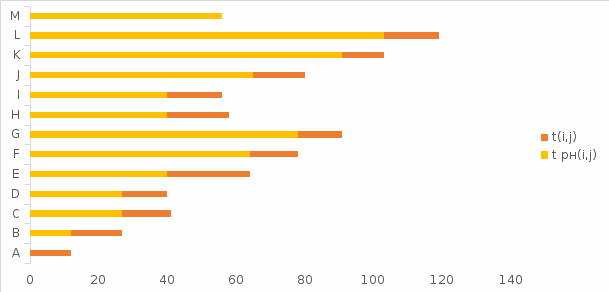 Теперь скроем часть графика, соответствующую ранним срокам начала работы. Для этого щелкаем на диаграмме на отображении, соответствующем ранним срокам начала работы, и выбираем «Формат ряда данных». В открывшемся окне настроек выбираем вкладку «Заливка» и активируем кнопку «Нет заливки». Получаем линейный график, характеризующий последовательность выполнения работ показанный на рис. 8.9. 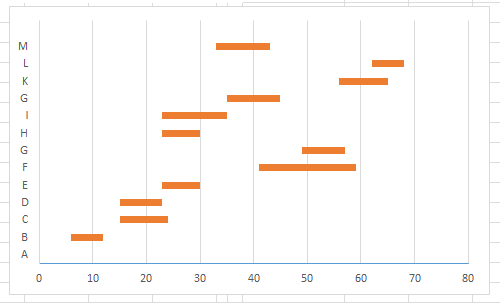 Найденные в результате расчета основные характеристики сетевого графика для событий и работ. Из полученных результатов расчета характеристик сетевого графика (таблица на рис 8.6) получаем, что для некритических работ 3-5 (С), 4-7 (Н), 4-6 (I) и 7-9 (J) сроки их выполнения можно варьировать. Эти работы могут начинаться с моментов времени, соответствующих найденным ранним срокам их начала (рис. 8.6). Допустимо сдвигать их начало до достижения поздних сроков начала. При этом общий (критический) срок выполнения всех работ комплекса не изменится. Так, работа 3-5 (С) может быть начата на 7-й единице времени, соответствующей раннему ее началу, или на 17-й единице времени позднего ее начала. В первом случае ее выполнение закончится на 7-й единице времени, а во втором – на 17-й единице. Допустимо также начать эту работу в любой момент времени из промежутка [7;17] без увеличения критического срока всех работ. Работу выполнил студент СФ, группы 080501-СВЗа-о21, Холматов Д.Н Работу принял доцент, к.т.н., Косиченко М.Ю. |