Надежность невосстанавливаемых элементов. 1 лаба Бекишов. Отчет по лабораторной работе надежность информационных систем Надежность невосстанавливаемых элементов
 Скачать 351.87 Kb. Скачать 351.87 Kb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего образования « Институт информатики и телекоммуникаций Кафедра информатики и вычислительной техники ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ Надежность информационных систем
Преподаватель подпись, дата инициалы, фамилия номер группы, зачетной книжки подпись, дата инициалы, фамилия 2022 г Цель работы: Определение количественных характеристик надежности невосстанавливаемых элементов информационных систем. Задачи работы: 1. Изучить показатели надежности невосстанавливаемого элемента. 2. Освоить методику расчетов показателей надежности невосстанавливаемых элементов по статистическим данным и по данным о законах распределения времени наработки на отказ. 3. Подготовить отчет о проделанной работе. Вариант задания к лабораторной работе Вариант №3 3. Время работы до отказа серийно выпускаемой детали распределено по нормальному закону с параметрами: m=1000 час, Ϭ=250 час. Определить: а) вероятность того, что деталь проработает безотказно 1200 часов; б) вероятность того, что безотказно проработав до момента времени 1200 часов, деталь безотказно проработает и до 1500 часов. Ход работы: а) 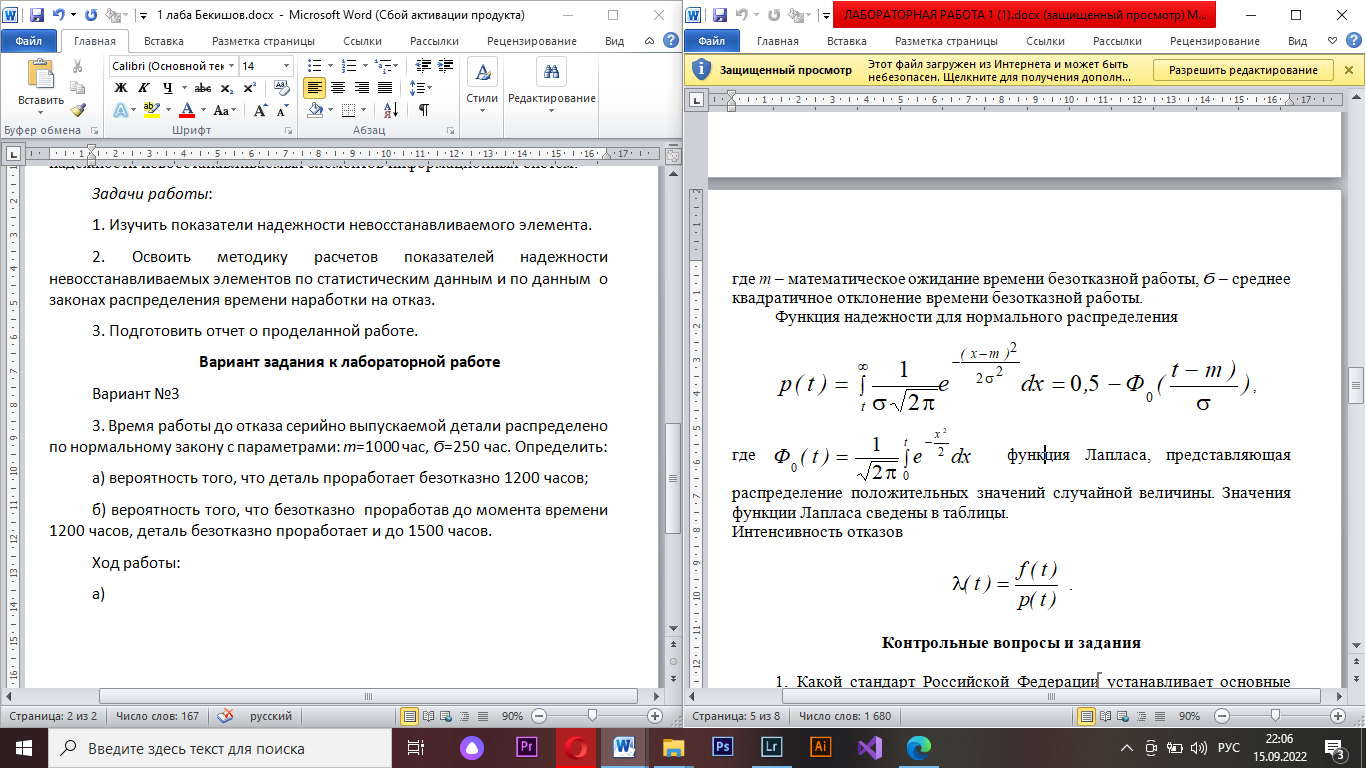 dx = 0.5-0.29 ((1200-1000) / 250) = 0.21 б) P((tb – ta) / ta) = P((1500-1200) / 1200) = 0.25 1. Какой стандарт Российской Федерации устанавливает основные понятия, термины и определения понятий в области надежности? ГОСТ 27.002-2015 2. Приведите определение понятия «надежность» в соответствии с ГОСТ. Надёжность – это свойство объекта сохранять во времени способность выполнять требуемые функции в заданных режимах и условиях применения, технического обслуживания, хранения и транспортирования. 3. Какие свойства объекта может включать в себя свойство «надежность»? включать в себя безотказность, ремонтопригодность, восстанавливаемость, долговечность, сохраняемость, готовность или определенные сочетания этих свойств. 4. Перечислите состояния, в которых может находиться объект в процессе эксплуатации. исправное состояние (исправность): Состояние объекта, в котором он соответствует всем требованиям, установленным в документации на него неисправное состояние (неисправность): Состояние объекта, в котором он не соответствует хотя бы одному из требований, установленных в документации на него 5. Дайте определение работоспособного состояния объекта. Состояние объекта, при котором значения всех параметров, характеризующих способность выполнять заданные функции, соответствует требованиям нормативно-технической и (или) конструкторской (проектной) документации. 6. Что такое отказ? событие, заключающееся в нарушении работоспособного состояния объекта 7. Какой объект называется невосстанавливаемым? Элемент относится к невосстанавливаемым, когда технический ремонт технически невозможен или экономически нецелесообразен. 8. По каким признакам можно выполнить классификацию отказов?
9. Какими показателями характеризуется надежность невосстанавливаемого элемента? p(t) – вероятность безотказной работы изделия на интервале времени от 0 до t; q(t) – вероятность отказа изделия на интервале времени от 0 до t; f(t) – частота отказов изделия или плотность вероятности времени безотказной работы изделия; λ(t) – интенсивность отказов изделия; mt – среднее время безотказной работы изделия. 10. Нарисуйте график функции надежности. 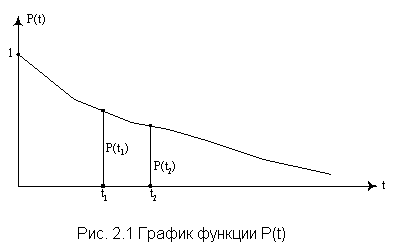 11. Назовите способы вычисления показателей надежности невосстанавливаемого элемента. 1) по статистическим данным об отказах; 2) использование теоретических распределений наработки до отказа. 12. Запишите формулу для определения статистической вероятности безотказной работы и статистической частоты отказов для невосстанавливаемого элемента. 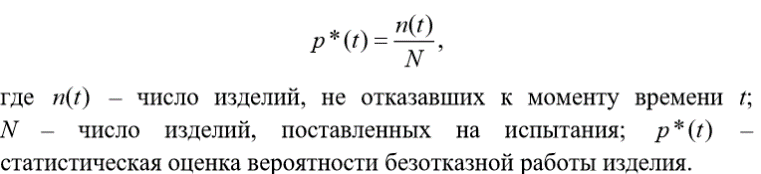 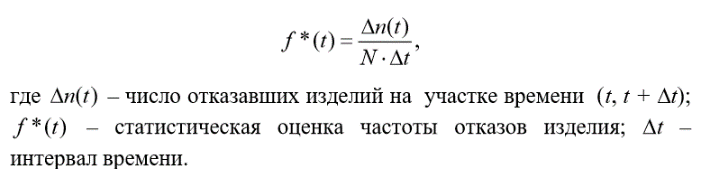 13. Каким образом можно определить вероятность того, что на интервале времени t произойдет n отказов? 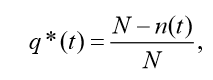  14. Приведите формулы для вычисления показателей надежности для экспоненциального закона распределения времени наработки. 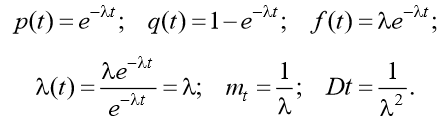 15. По каким формулам вычисляются показатели надежности для нормального закона распределения времени наработки?  |

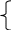 период приработки
период приработки