аио1. Отчёт по Лабораторной работе по дисциплине Адаптивные и оптимальные системы управления Практическая работа 1 Экстремумы функций нескольких переменных
 Скачать 303.29 Kb. Скачать 303.29 Kb.
|
 Институт кибернетики Институт кибернетикиКафедра автоматических систем (АС) _________________________________________________________________ Отчёт по Лабораторной работе по дисциплине: «Адаптивные и оптимальные системы управления» Практическая работа №1 «Экстремумы функций нескольких переменных»
Москва 2020 Вариант 1.  Компьютерное моделирование 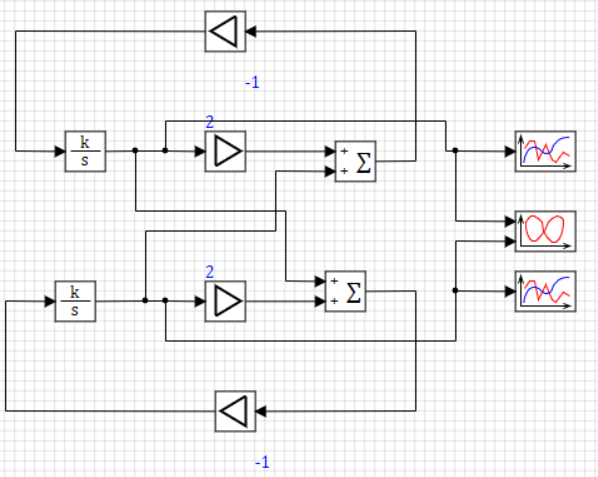 Значение Х Значение Y 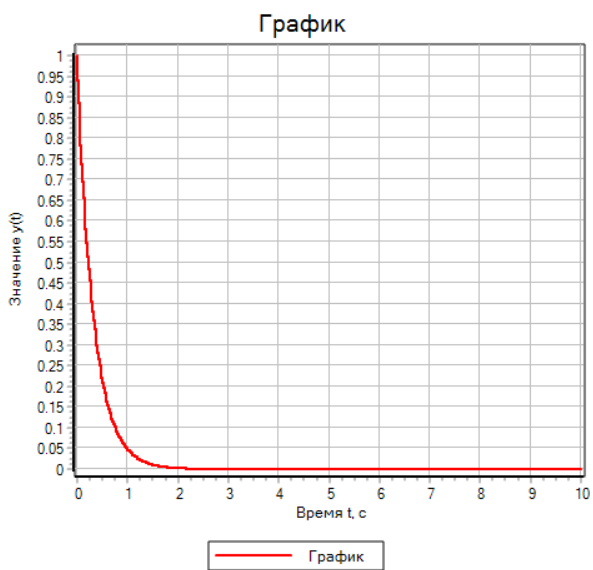  Фазовый портрет  Найти все экстремумы функции на множестве. Метод решения подобных задач основан на теореме, которую принято называть принципом Лагранжа. Для того, чтобы воспользоваться этим принципом, нужно создать так называемую функцию Лагранжа: 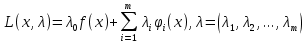 Коэффициенты 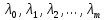 называются множителями Лагранжа. Их величина будет определена позднее. называются множителями Лагранжа. Их величина будет определена позднее.Принцип говорит о том, что если точка x0 является точкой условного экстремума, то существует не равный нулю вектор , при котором производная функции Лагранжа обращается в ноль, т.е. 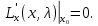 Основываясь на теореме Лагранжа, решим поставленную задачу. Для этого поступаем следующим образом 1) Составляем функцию Лагранжа: 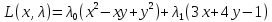 2) Записываем необходимое условие экстремума: 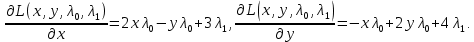 После этого нужно решать систему 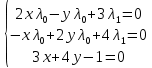 Рассмотрим два случая. a) Пусть λ0 = 0. Тогда система принимает вид 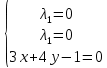 Она разрешима лишь при λ1 = 0. Следовательно, λ = (0, 0), и в этом случае подозрительных на экстремум точек нет. б) Пусть λ0 0. Тогда можно положить λ0 = 1: 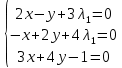 Из последней системы вытекает, что 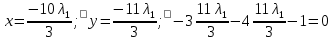 Значит 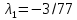 , и подозрительные точки на экстремумы. , и подозрительные точки на экстремумы.(x,y)=( 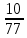 , ,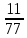 ,) ,) | |||||||||||||||||||||

