Лабораторная 1 СЭС. СС1_Кожаева О.Р. ЭЭ21-03С-ЭБ (1). Отчет по лабораторной работе по Социальноэкономической статистике модуль Социальная статистика
 Скачать 38.1 Kb. Скачать 38.1 Kb.
|
|
Федеральное государственное автономное образовательное учреждение высшего образования «СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ» Институт экономики, государственного управления и финансов Кафедра управления человеческими ресурсами ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ по Социально-экономической статистике модуль «Социальная статистика» СТАТИСТИКА ДОХОДОВ НАСЕЛЕНИЯ Преподаватель __________ Е.Г. Григорьева подпись, дата Студент ЭЭ21-03С-ЭБ __________ Кожаева О.Р. номер группы, зачетной книжки подпись, дата инициалы, фамилия Красноярск 2022 Статистическое исследование зависимости между средним временем ожидания транспорта и успеваемостью студентов Цель лабораторной работы – провести анализ дифференциации среднедушевых денежных доходов в Курской области за 2015 и 2020 год и оценить их динамику. Для достижения цели необходимо выполнить такие задачи, как: Рассчитать показатели средней, моды, медианы для интервальных таблиц; Провести анализ дифференциации и концентрации доходов; Построить кривые Лоренца за два года; Сформировать выводы на основе проделанного исследования. Для исследования рассмотрены показатели доходов населения Курской области. Таблица 1 – Распределение численности населения по величине среднедушевых денежных доходов в 2015 году. (в процентах от общей численности населения субъекта)
Далее исследуем полученные результаты опроса, отнеся их к номинальной шкале. Значит, необходимо рассчитать непараметрический критерий χ2 и коэффициенты взаимной сопряженности Пирсона и Чупрова. Если рассчитанное значение χ2, превышает табличное, то можно утверждать о том, что связь между факторами не случайна, то есть выполняется гипотеза Н1. Значение непараметрического критерия χ2 рассчитывается по формуле: 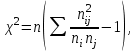 где гдеni – суммы показателей по строкам; nj – суммы показателей по столбцам; nij – исходные показатели в таблице; n – общее число признаков. Рассчитаем непараметрического критерия χ2: 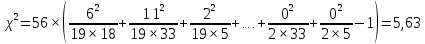 Табличное значение непараметрического критерия χ2 определяется с учетом числа степеней свободы υ и уровня значимости α. Число степеней свободы учитывает размерность таблицы: 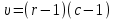 , где r – число строк, с – число столбцов таблицы. , где r – число строк, с – число столбцов таблицы.Для наших целей уровень значимости достаточен на уровне 5 %. 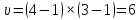 При уровне значимости 0,05 и числе степеней свободы υ = 6 табличное значение составляет 12,5916. 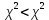 табл таблТаким образом, рассчитанное значение непараметрического критерия χ2 меньше табличного, следовательно, верной является гипотеза H0 – зависимость между средним временем ожидания транспорта и успеваемостью студентов отсутствует. Для степени тесноты связи между качественными признаками используются: Коэффициент Пирсона 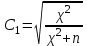 , ,Рассчитаем коэффициент: 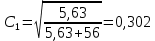 Коэффициент Чупрова 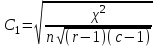 . .Рассчитываем коэффициент Чупрова: 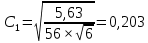 Считается, что коэффициент Чупрова более точен, так как он учитывает размерность таблицы. Используются следующие критерии: если значения обоих коэффициентов больше либо равны 0,3, то принимается гипотеза Н1, в любом другом случае выполняется гипотеза Н0. Значения коэффициента Чупрова меньше 0,3, поэтому принимается гипотеза Н0 – между средним временем ожидания транспорта и успеваемостью студентов зависимость отсутствует. Вывод: По рассчитанным коэффициентам пришли к выводу о том, что между средним временем ожидания транспорта и успеваемостью студентов отсутствует зависимость. Рассчитанный коэффициент Пирсона составил 0,302, а коэффициент Чупрова равен 0,203, так как рассчитанное значение коэффициента Чупрова меньше 0,3, то приняли гипотезу об отсутствии зависимости между рассматриваемыми признаками. По сводной таблице отметим, что 19 студентов из 56 студентов не ожидают транспортное средство, то есть у данных студентов, скорее всего, есть свое личное транспортное средство, либо они добираются пешком. Приложение 1 – Результаты опроса студентов Таблица 1 – Результаты исследования
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
