Отчет. Отчет по летней учебной практике Вариант 9 Выполнил Студент гр. 0А94 Т. М. Ворсина подпись дата

• Название: Отчет по летней учебной практике Вариант 9 Выполнил Студент гр. 0А94 Т. М. Ворсина подпись дата
• Дата: 22.07.2022
• Размер: 4.21 Mb.
• Имя файла: Отчет.doc
• Тип: Отчет; #634854

Министерство образования и науки Российской Федерации

Федеральное государственное автономное образовательное учреждение

высшего образования

«НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ

ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Школа ИЯТШ

Отделение ЯТЦ

Направление 14.03.02 «Ядерные физика и технологии»


Отчет по летней учебной практике

Вариант 9

Выполнил

Студент гр. 0А94 ________ ________ Т.М. Ворсина

подпись дата
Проверил

Преподаватель _______ ________ А.В. Богданов

подпись дата


Томск 2020

Оглавление

Оглавление 1

Цели работы 2

Теоретическая часть 2

Пакет Mathematica как инженерный калькулятор 2

Численное и аналитическое решение уравнений и систем уравнений, простейшее редактирование текста 3

Создание списков 3

Работа с векторами и матрицами 4

Расширенная работа со списками 4

Функции математического анализа, преобразования выражений и подстановки в выражениях 6

Построение графиков функций, заданных аналитическими формулами 7

Построение графиков по табличным данным 9

Аналитическое решение дифференциальных уравнений и систем дифференциальных уравнений 10

Обработка экспериментальных данных 11

Динамические объекты 12

Экспериментальная часть 15

Лабораторная работа №1 15

Лабораторная работа №2 16

Лабораторная работа №3 16

Лабораторная работа №4 17

Лабораторная работа №5 19

Лабораторная работа №6 20

Лабораторная работа №7 21

Лабораторная работа №8 24

Лабораторная работа №9 25

Лабораторная работа №10 28

Заключение 29

Цели работы

1. Научиться работать в пакете Mathematica.

2. Использовать его как простой и инженерный калькулятор.

3. Решать с помощью его линейные, трансцендентные, дифференциальные уравнения и системы, состоящие из них.

4. Строить двухмерные и трёхмерные графики функций, заданных как аналитически, так и из табличных (экспериментальных) данных.

5. Научиться пользоваться функциями математического анализа.

Теоретическая часть

Пакет Mathematica как инженерный калькулятор

Пакет Mathematica представляет собой символьную (аналитическую) математическую систему, то есть вычисления в первую очередь производятся в символьном виде (вычисления производятся над формулами).

Пакет Mathematica можно использовать как простой калькулятор с помощью простых встроенных математических операций (+, -, *, /, ^).





Также его можно использовать как инженерный калькулятор с помощью встроенных функций к примеру Sin[], Cos[], Log[], ArcTan[].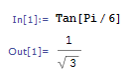





Как видно из примеров результат выводится аналитически, если не может быть посчитан точно численно, чтобы посчитать численно результат вычислений требуется использовать функцию N[].



Так же из примеров видно, что пакет Mathematica считает тригонометрические функции принимая за аргумент в радианах. Для перевода чисел из градусов в радианы существует функция Degree.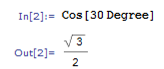



Так пакет Mathematica ограничен в точности вычислениях только компьютером, на котором производятся вычисления, то эту точность можно регулировать.



Как видно из примера, второй аргумент этой функции является точность (количество знаков в числе) вычислений.

Иногда бывает необходимо измерить, за какое время пакет Mathematica произведёт те или иные расчёты. Для этого используется функция Timing[].



Из примера видно, что первым числом является время выполнения операции, а вторым результат операции.

Численное и аналитическое решение уравнений и систем уравнений, простейшее редактирование текста

Для решения уравнений и систем уравнений используются функции "Roots[уравнение, переменная]" и "Solve[уравнения, переменные]". Первая функция находит решение полиноминальных уравнений. Вторая функция находит решение различных типов уравнений и систем уравнений.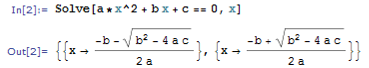





Также эти функции могут находить решение систем уравнений.



Некоторые уравнения не могут быть решены аналитически функцией “Solve[]”. Для нахождения приближённого значения корня уравнения используется функция "FindRoot[уравнение, {переменная, начальное приближение к корню}]".



В пакет Mathematica встроены функции редактирования текста. Меню “Format->Style”, позволяет редактировать стиль ячейки (“Title”, “Subtitle”, “Section”, ...). Также в меню “Format” можно в можно выбрать размер текста “Size”, цвет текста “Text Color”, его положение на листе “Text Alignment”, фон за текстом “Backgrount Color” и т.д.. Также можно разрывать страницы командой “Insert->Page Break”.

Создание списков

В пакете Mathematica существует множество функций для работы со списками. Список - способ структурирования данных. Список можно задать с помощью функции "List[a₁, a₂, a₃, ..., a_n]", где a_i - любое значение вносимое в список, а также с помощью фигурных скобок "{a₁, a₂, a₃, ..., a_n }".



Списки можно представлять в виде таблиц и матриц с помощью команд "TableForm[s]" и "MatrixForm[s]" соответственно, где s - список.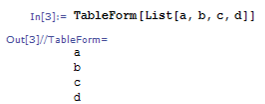





Также есть функции создающие списки по каким-либо правилам. Функция "Range[min, max, step]" - создаёт список с одного значения “min” до другого “max” с заданным шагом “step”.



"Table[f(x₁, x₂, ..., x_n), {x₁, min₁, max₁, step₁}, {x₂, min₂, max₂, step₂}, ..., {x_n, min_n, max_n, step_n}]" - создаёт список по функции f(x₁, x₂, ..., x_n), где x_i - переменная, min_i - минимальное значение переменной x_i, max_i - максимальное значение переменной x_i, step_i - шаг переменной x_i.



"DiagonalMatrix[s]" - создаёт двумерную диагональную матрицу, располагая элементы списка “s” на главное диагонали.



Также списки можно создавать импортируя данные из файла с помощью функции "Import["полный путь к файлу", "формат чтения"]", полный путь к файлу включает его имя и расширение, формат чтения "List" либо "Table". Первый считывает данные в виде списка, второй в виде таблицы.

Работа с векторами и матрицами

Вектора в пакете Mathematica - это списки вида "{a₁, a₂, a₃}", а матрицы - списки списков вида "{{a₁, a₂, ..., a_n}, {b₁, b₂, ..., b_n}, ..., {{m₁, m₂, ..., m_n}". В пакете Mathematica есть функции для работы с векторами и матрицами. Для сложения и вычитания векторов с векторами, матриц с матрицами применяются операции сложения "+" и вычитания "-". Функция Dot[a, b] скалярно умножает вектор "a" на вектор "b" или умножает матрицу "а" на матрицу "b". Функция Cross[a, b] векторно умножает вектор "a" на вектор "b".





Функция "Norm[a]" находит длину вектора "a".



Функция Det[a] находит определитель квадратной матрицы "a".



Функция "Transpose[a]" находит транспонированную матрицу "a".



Функция "Inverse[a]" вычисляет матрицу обратную матрицы "a".



Функция "MatrixPower[a, n]" вычисляет матрицу равную матрице "a" возведённую в целую положительную степень "n".

Расширенная работа со списками

В пакете Mathematica возможно выполнять множество операций над списками. Функция "VectorQ[s]" проверяет, является ли список "s" списком без вложенных списков (вектором).



Функция "Length[s]" возвращает значение количества элементов в списке "s".



Функция "Count[s, условие]" возвращает значение количества элементов списка "s", удовлетворяющих "условию".



Функция "Position[s, условие]" возвращает номера позиций элементов списка "s", удовлетворяющих условию.



В обоих этих функциях в условии можно написать "_Integer", "_Real", "_Complex" и т. д. для целых, вещественных, комплексных типов данных соответственно.

Функция "Select[s, условие]" возвращает элементы списка "s", которые удовлетворяют "условию".



Функция "Part[s, i]" выводит элемент списка "s", стоящий на i-ой позиции. Если вместо одой позиции "i" указать список позиций "i₁,i₂, ..., i_n", то функция выведет список со значениями элементов списка "s", стоящих на "i₁,i₂, ..., i_n-ых позициях.



Функция "DeleteCases[s, условие]" удаляет элемнты списка "s" удовлетворяющие "условию".



Функция "Sort[s, условие]" сортирует список "s" по условию, если нет "условия" сортирует список "s" по возрастанию, если в "условие" написать "Greater", то сортировка будет по убыванию значений элементов списка "s".



Функция "Join[s₁, s₂, ..., s_n]" объединяет списки "s₁, s₂, ..., s_n" в один список.



Функция "Union[s₁, s₂, ..., s_n]" объединяет списки "s₁, s₂, ..., s_n" в один список, сортируя его по возрастанию значений элементов в нём, удаляя повторяющиеся элементы.



Функция "Intersection[s₁, s₂, ..., s_n]" выводит список, отсортированный по возрастанию значений элементов, состоящий из элементов, которые есть во всех списках.



Функция "Complement[s₁, s₂, ..., s_n]" выводит список, отсортированный по возрастанию значений элементов, который состоит из элементов, которые есть только в первом списке.

Функции математического анализа, преобразования выражений и подстановки в выражениях

В пакете Mathematica существует множество функция для преобразования выражений и их упрощения.

К функциям упрощения выражений относятся 2 функции. Функция "Simplify[s]" упрощает выражение "s". Функция "FullSimplify[s]" упрощает выражения, использовав специальные функции. Также, в особо простых выражениях пакет Mathematica сам упрощает выражение в момент просчёта команды.





Функций для преобразования выражений больше чем функций для их упрощения. Функция "Expand[s, f(x)]" раскрывает скобки типа полином на полином в выражении "s", а также целые положительные степени (что и является полиномом, умноженным на полином), но не раскрывает скобки, содержащие выражение отличное от "f(x)", если f(x) отсутствует, то раскрывает все скобки.



"PowerExpand[s]" - раскрывает различные степени и логарифмы произведений в выражении "s".



Это не все функции для раскрытия выражений, существует целый класс функций "Expand". "Factor[s]" - раскладывает полиномы, содержащиеся в выражении "s", на множители. Эта функция обратная функции "Expand[s]".



Также пакет Mathematica способен выполнять операции математического анализа: считать пределы, суммы, произведения, находить интеграл и дифференциал как полный различных порядков, так и частный, также различных порядков.

Для вычисления пределов существует функция "Limit[f(x), x->x₀/ ±Infinity]", которая вычисляет предел функции "f(x)", при стремлении "x" к "x₀" (числу) или плюс (минус) бесконечности.



Функция "Sum[f(i, j, ..., k), {i, i_min, i_max, n_i}, {j, j_min, j_max, n_j}, ..., {k, k_min, k_max, n_k}] вычисляет сумму значений функции "f(i, j, ..., k)" зависящую от "i, j, ..., k" от "i_min, j_min, ..., k_min" до " i_max, j_min, ..., k_max" с шагом "n_i, n_j, ..., n_k". Если не указывать шаг он будет равен 1. "Product[f(i, j, ..., k), {i, i_min, i_max, n_i}, {j, j_min, j_max, n_j}, ..., {k, k_min, k_max, n_k}] вычисляет произведение значений функции "f(i, j, ..., k)" зависящию от "i, j, ..., k" от "i_min, j_min, ..., k_min" до " i_max, j_min, ..., k_max" с шагом "n_i, n_j, ..., n_k". Если не указывать шаг он будет равен 1. Если перед этими функциями дописать N (то есть записать "NSum" и "NProduct"), то значения вычислений будут представлены в численном виде.





Функция "Integrate[f(x₁,x₂, ..., x_n), x₁, x₂, ..., x_n]" вычисляет неопределённый интеграл n-ой кратности от функции "f(x₁,x₂, ..., x_n)", зависящей от "x₁, x₂, ..., x_n". Функция "Integrate[f(x₁, x₂, ..., x_n), {x₁, x_1min, x_1max}, {x₂, x_2min, x_2max}, ..., {x_n, x_nmin, x_nmax}]" вычисляет определённый интеграл n-ой кратности от функции "f(x₁,x₂, ..., x_n)", зависящей от "x₁, x₂, ..., x_n" от "x_1min, x_2min, ..., x_nmin" до " x_1max, x_2min, ..., x_nmax".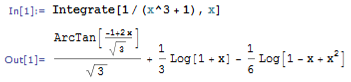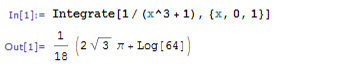





Функция "D[f(x₁, x₂, ..., x_n), {x₁, mx₁}, {x₂, mx₂}, ..., {x_n, mx_n}]", вычисляет частную производную функции "f(x₁, x₂, ..., x_n)" зависящей от "x₁, x₂, ..., x_n" порядка "mx₁, mx₂, ..., mx_n". Для этой функции существует опция “NonConstants”, с помощью которой можно задать список символьных выражений не явно зависящих от переменный дифференцирования "x₁, x₂, ..., x_n". По умолчанию все остальные символьные выражения считаются константам.



Функция "Dt[f(x₁, x₂, ..., x_n)]" вычисляет полный дифференциал функции "f(x₁, x₂, ..., x_n)". Для этой функции существует опция “Constants”, так функция считает все символьные выражение неявно зависящими от переменных дифференцирования, с помощью которой можно указать какие символьные выражения нужно считать не зависимыми от переменных дифференцирования.



В пакете Mathematica существуют функции для замены переменных другими переменными или числами. Одна из них функция "ReplaceAll[s, n->m]", она заменяет в выражении "s" переменную "n" на "m".



Её можно использовать для проверки правильности решения уравнений в виде "ReplaceAll[s, n]", где "s" - уравнение, решение которого нужно проверить, "n" - корень, или, если задать "n" списком, то он проверит все корни. Если корень обращает уравнение в тождество, то будет выведено "True", если нет, то будет выведено "Falce". Если требуется проверить уравнение численно, то в прошлой записи "s" должно быть не уравнением, а выражением.

Построение графиков функций, заданных аналитическими формулами

Многие физические процессы можно анализировать исходя из графиков этих процесов. Для их построения в пакете Mathematica существует множество функций.

Для построения графиков вида y=f(x) используется функция "Plot[f(x), {x, x_min, x_max}]", где "f(x)" - некоторая функция, график которой строется для x от x_min до x_max. Для параметрически заданных функций используется функция "ParametricPlot[{x(t), y(t)}, {t, t_min, t_max}]", где "x(t)" и "y(t)" некоторые функции, график строится в пределах по "t" от "t_min" до "t_max".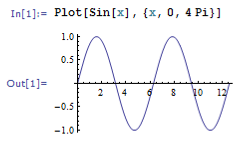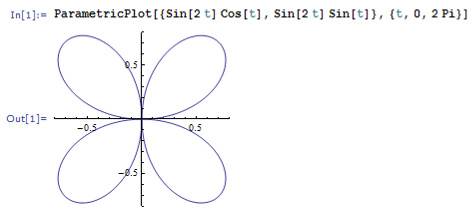





Для построения трёх мерных графиков вида z=f(x, y) используется функция "Plot3D[f(x, y), {x, x_min, x_max}, {y, y_min, y_max}]", где f(x, y) некоторая функция, график которой строется в пределах по "x" от "x_min", до "x_max", в пределах по "y" от "y_min", до "y_max". Функция "ParametricPlot3D[{x(u,v), y(u, v), z(u, v)}, {u, u_min, u_max},{v, v_min, v_max}]" строит график функции x=x(u,v), y=y(u, v), z=z(u, v) (тоесть параметрически заданную функцию), в пределах по "u" от "u_min", до "u_max", в пределах по "v" от "v_min", до "v_max". Если функция будет зависеть от одного параметра, то её графиком будет кривая.





Для построения контурных графиков используется функция "ContourPlot[]", её синтаксис аналогичен функции "Plot3D[]". Для построения графика плотности используется функция "DensityPlot[]", её синтаксис аналогичен функции "Plot3D[]".





Для всех этих функций существует множество опций. Их можно узнать, набрав "Options[Plot]". "AspectRation->k/Automatic" задаёт отношение высоты к ширине для двухмерного графика. Изначально задано значение 1.618, это является отношением 1 к константе золотого свечения. "AxesLabel->{"s₁","s₂"}" задаёт подписи к горизонтальной оси название "s₁", к вертикальной "s₂". "Frame->", если задать "True", то будет построена прямоугольная рамка вокруг графика. "FrameLabel->{"s₁","s₂"}" задаёт подписи к нижней горизонтальной линии рамки название "s₁", к левой вертикальной "s₂". Всего можно ввести 4 параметра, на все линии рамки. "RotateLabe->" если задать "False", то название боковых линий рамки не будет разворачиваться на 90°, по умолчанию "True". "PlotLabe->"s"" выводит название графика. "GridLines->None/Automatic/{x, y}" отображает сетку на графике. Если задать "None", не отображает сетку на графике, если "Automatic", то расстояние между линиями задаётся автоматически, если ввести {x, y}, то расстояние между линиями сетки по горизонтальной оси будет "x", а по вертикальной "y".

Опция "Background->s" задаёт цвет фона, на котором строится график, вместо "s" используется любая из функций для задания цвета, то есть "GrayLevel[s]", задаёт оттенки серого цвета, "s" принимает значения от 0 (чёрный) до 1 (белый). RGBColor[R, G, B] задаёт цвет смешением красного "R", зелёного "G" и синего "B", параметры принимают значение от 0 до 1. CMYKColor[C, M, Y, K] тоже самое, что и "RGBColor[]", только цвет задаёт смешением синего "C", пурпурного "M", жёлтого "Y" и чёрного "K". Опция "PlotStyle->s" задаёт цвет и тип линии графика. Цвет задаётся аналогично опции "Background". "Thickness[s]" задаёт толщину линии, значение "s" от 0 до 1, это толщина относительно размера графика. Если требуется указать толщину в абсолютных единицах, применяется функция "AbsoluteThickness[s]", где "s" - толщина линии. "Dashing[{s₁,s₂,...,s_n}]" задаёт длину построенных и не построенных элементов линии графика, "s_2n-1" (номер позиции нечётный) задаёт длину построенной части графика, "s_2n" (номер позиции чётный) задаёт длину не построенной части графика, этот шаблон повторяется циклически до конца графика. Значение "s_i" изменяется от 0 до 1, длина измеряется в относительных единицах аналогично функции "Thickness[]". Если требуется указать длину в абсолютных величинах, то нужно поступить как с функцией "Thickness[]". "PointSize[s]" задаёт размер точек графика, "s" принимает значения от 0 до 1, размер точек измеряется в относительных единицах аналогично функции "Thickness[]". Если требуется указать размер точек в абсолютных величинах, то нужно поступить как с функцией "Thickness[]". Опция "FrameStyle->s" задаёт стиль рамки вокруг графика, аналогично опции "PlotStyle->s".

Построение графиков по табличным данным

Так как большинство данных мы получаем из экспериментов, то мы должны строить по этим данным графики для их анализа. Обычно эти данные представлены в виде таблиц, матриц, списков. В пакете Mathematica существуют функции для выполнения подобных задач.

Для построения 2-ух мерного графика по табличным данным используется функция "ListPlot[s]", где "s" - таблица с одним или двумя столбцами. Если столбец один, то есть это обычный список, его значения принимаются за значения на оси "y", по оси "x" берётся ряд натуральных чисел, если таблица состоит из 2-ух столбцов, то значения первого берутся значениями по оси "x", а второго по оси "y". Построенный график будет представлен в виде множества точек. Чтобы эти почки были соединены линиями между собой требуется ввести опцию "Joined->True", либо построить график с помощью специальной функции "ListLinePlot[s]", синтаксис которой аналогичен функции "ListPlot[]".



Для построения 3-ёх мерных графиков по табличным данным используется функция "ListPlot3D[s]", где "s" - таблица с тремя столбцами, значения первого это значения по оси "x", второго по "y", третьего по "z".



Для построения контурного графика по данным таблицы используется функция "ListContourPlot[s]", синтаксис аналогичен функции "ListPlot3D[]". Для построения графиков плотности по табличным данным используется функция "ListDensityPlot[s]", синтаксис аналогичен функции "ListPlot3D[]".

Большинство процессов происходящих в природе можно описать дифференциальными уравнениями. Так что для их анализа нужно решать дифференциальные уравнения, но большинство из них имеют не простое решение, а некоторые вообще нельзя решить. В пакете Mathematica существуют функции для решения дифференциальных уравнений.

Аналитическое решение дифференциальных уравнений и систем дифференциальных уравнений

Для решения дифференциальных уравнений в общем виде существует функция "DSolve[f[t, x, x', x'', ..., x⁽ⁿ⁾]=g[t, x, x', x'', ..., x^(m)], x[t], t]", где "f[t, x, x', x'', ..., x⁽ⁿ⁾]=g[t, x, x', x'', ..., x^(m)" - некоторое дифференциальное уравнение, "x[t]" - переменная относительно которой надо решить уравнение, "t" - независимая переменная, от которой зависит "x".



Если задано начальные условия, то они записываются вместе с дифференциальным уравнением как система уравнений в функции "Solve[]", то есть "DSolve[{f[t, x, x', x'', ..., x⁽ⁿ⁾]=g[t, x, x', x'', ..., x^(m)], x[0]=x₀, x'[0]=x'₀, ..., x^(n)[0]=x^(n)₀}, x[t], t]", где (x^(i))[0]=x^(i)₀ - некоторые начальные условия. Для решения систем дифференциальных уравнений применяется такая же запись, только вместо начальных условий записываются уравнения системы, то есть "DSolve[{f₁[t, x₁, x₁', ..., x₁^(n­1­), x₂, x₂', ..., x₂⁽ⁿ²⁾, ..., xk, xk', ..., x_k^(nk)]=g₁[t,x₁, x₁', ..., x₁^(m1), x₂, x₂', ..., x₂^(m2), ..., x_k, x_k', ..., x_k^(mk)], f₂[t, x₁, x₁', ..., x₁⁽ⁿ¹⁾, x₂, x₂', ..., x₂⁽ⁿ²⁾, ..., x_k, x_k', ..., x_k^(nk)]=g₂[t,x₁, x₁', ..., x₁^(m1), x₂, x₂', ..., x₂^(m2), ..., x_k, x_k', ..., x_k^(mk), ..., }, {x₁[t], x₂[t], ... x_k[t]}, t]".



Так как некоторые дифференциальные уравнения не имеют аналитических решений, то для их решения применяют численные методы. Для численного решения дифференциального уравнения применяют функцию "NDSolve[]", аргументы этой функции аналогичны функции "DSolve[]", за исключением последнего, он выглядит так: {t, t_min, t_max}, он задаёт в от какого "t_min" и до какого t_max" искать решение. Также обязательно должны быть численно указаны начальные условия.

Обработка экспериментальных данных

Так как большинство данных мы получаем из экспериментов, то их нужно как-то анализировать, обрабатывать и работать с ними. Чаще всего эти данные представлены в виде таблиц. В пакете Mathematica есть множество функций для подобной работы.

Функция "Total[s]" вычисляет сумму всех элементов списка "s". "Mean[s]" вычисляет среднее значение в списке "s". "Variance[s]" вычисляет дисперсию (квадрат среднеквадратичного отклонения) в списке "s".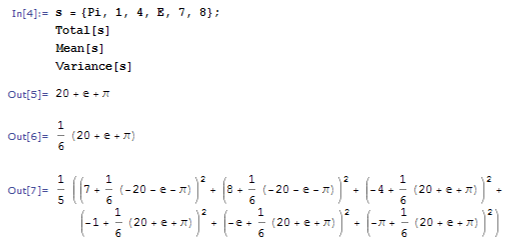



Иногда требуется предсказать, как ведёт себя функция в промежутках между точками. В пакете Mathematica есть функция для выполнения этой задачи. Функция "Interpolation[s]" строит интерполяционный полином по данным таблицы "s", если в таблице только один столбец, то он принимается за значения "f(x)", а "x" принимает значения ряда натуральных чисел. Если в таблице два столбца, то первый из них рассматривается как значения "x", а второй "f(x)".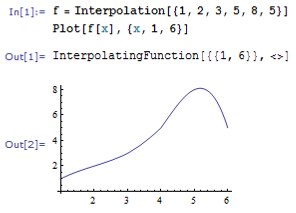



Для этой функции существуют различные опции. "InterpolationOrder->k" задаёт порядок полинома интерполирования. "Method->s" задаёт метод интерполирования "s". "PeriodicInterpolation->s" задаёт периодичность функции, если "s" "True", то функция будет периодичной, по умолчанию "False".

Для получения аналитически заданной функции (уравнения) используется функция "Fit[s, {f1(x), f2(x), ..., fn(x)}, x]", находит методом наименьших квадратов лиейную комбинацию функций "f1(x), f2(x), ..., fn(x)", по переменной x. Также можно использовать функции нескольких переменных, только нужно задать список по каким переменным искать функцию.



Функция "FindFit[s, f(x, q1, q2, ..., qn), {q1, q2, ..., qn}, x]" находит коэффициенты "q1, q2, ..., qn" к функции заранее известного вида "f(x, q1, q2, ..., qn)".

Динамические объекты

Так большинство в большинстве решаемых задач есть параметры, то нужно как-то уметь их регулировать не по ходу решения, а непосредственно в ответе. В пакете Mathematica встроено много динамических функций, предназначенных именно для этого.

Самым простым динамическим объектом является ползунок. Функции его отображения “Slider[x₀/Dynamic[x]]”. “Dynamic[x]” – делает переменную “x” динамично изменяющуюся, то есть при изменении переменной “x”, её изменение тоже отобразится, без дополнительного просчёта программы.



С помощью этой функции и её опций можно создавать изменяющиеся графики функций. Но она изменяет значение функции всегда, до того пока ядро не будет выгружено. Что бы использовать динамическую переменную только в одном объекте необходимо воспользоваться функцией “DynamicModule[{x,y, …}, {любые функции}]”. Необходимо помнить, что, чтобы необходимый объект был динамически изменяем, необходимо пользоваться функцией “Dynamic[]”.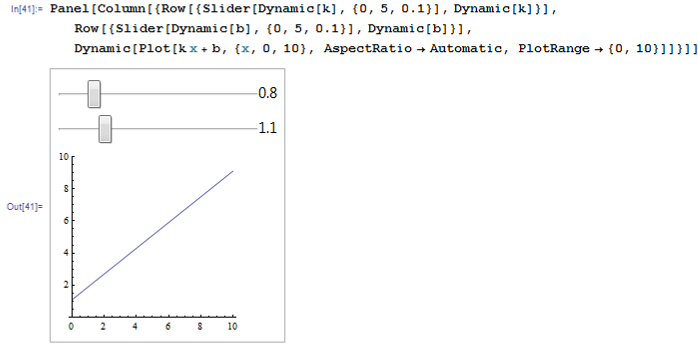





Следующие динамические объекты это кнопки. Их можно создать функцией “Button[s, f]”, где “s” – надпись на кнопке, “f” – выполняемая функция после нажатия кнопки.



Также существуют флажки, функция “Checkbox[s, f]”, переключатели, функция “RadioButton[Dynamical[x], f]”, принимают значение “True”, “False”, при значении “True” выполняется функция “x=f”. Также существуют двух мерные ползунки функция “Slider2D[]”, синтаксис аналогичен обычным ползункам.

Всё это простые динамические функции. Функция для создания динамически изменяющегося графика довольно-таки сложна, но есть функция, которая выполняет подобные задачи, но более лёгкая в синтаксисе. Эта функция “Manipulate[f(a, b, …), {a, a_min, a_max, a_d}, …]”, где “f(a, b, …) любая функция в которой есть динамические параметры, изменяющиеся от a_min до a_max, с шагом a_d. Также можно выбрать тип контролера опцией “ControlType->”.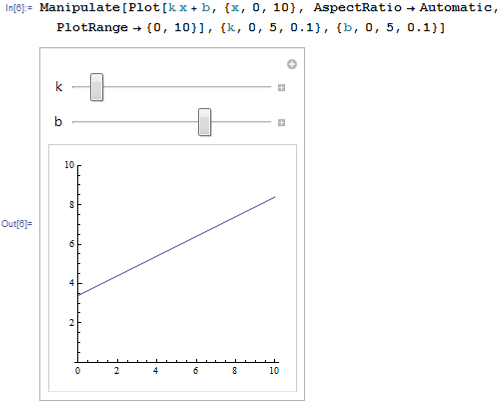



В функции “Manipulate[]” встроена опция “проигрывания”, но в ней мало настроек. Для более гибкой настройки применяется функция “Animate[]”, синтаксис аналогичен функции “Manipulate[]”, только добавляются опции для этой функции.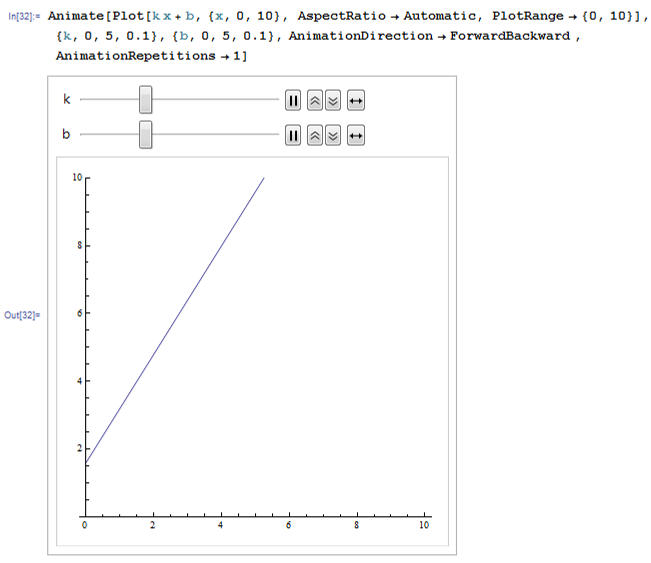



Также для изменения переменных существует функция “Control[]”, от её синтаксиса зависит, какой контролер будет управлять переменной.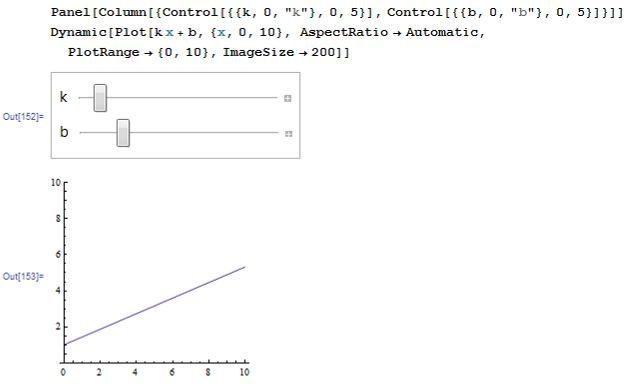



Также в пакете Mathematica существует много разновидностей выпадающих меню. Одно из них вызывается функцией “MenuView[]”. Оно отвечает за выбор первого, второго и т. д. действий.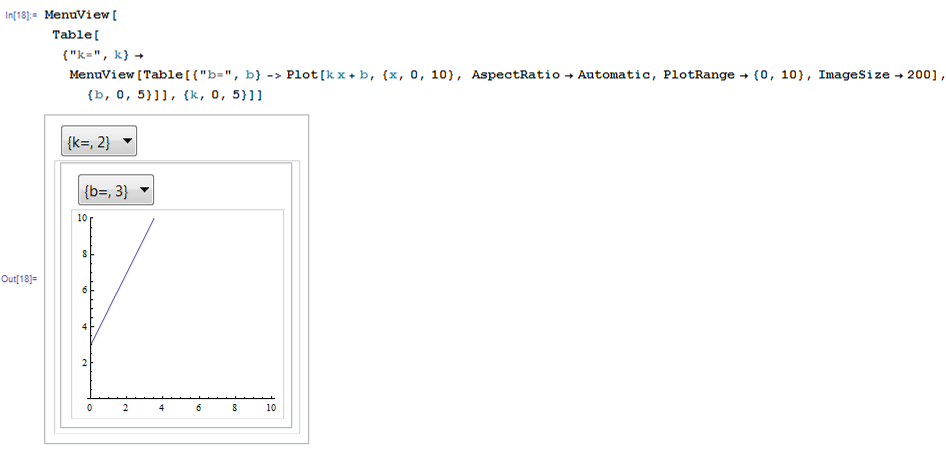



Также существует динамическое изменение с помощью таблицы с кнопками. Функция вызывающая её “TabView[]”.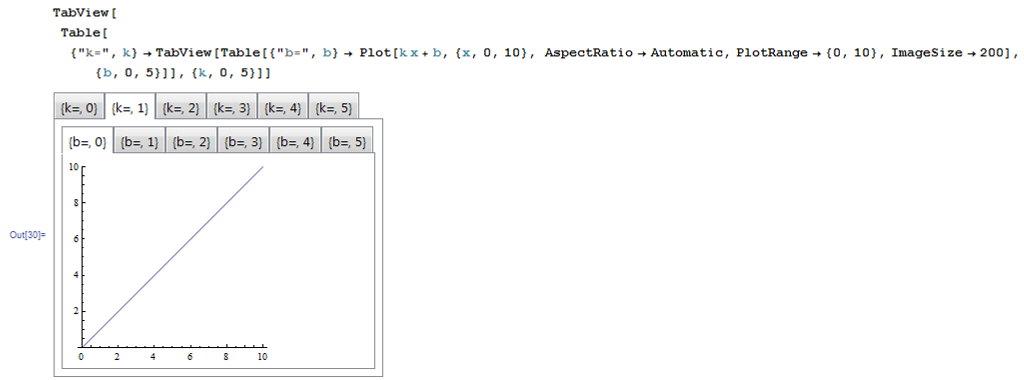



В пакете Mathematica существует ещё множество динамических функций, но рассказать про все практически не возможно, также к ним есть огромное количество опций. Про всё более подробно можно узнать в справке пакета Mathematica. Все эти функции лучше подходят для решения не одной задачи, как видно из примеров, для построения графиков лучший выбор это функция “Manipulate[]”, а совершенно разных. Я специально показал выполнение одной и той же задачи разными функциями, для того чтобы было видно, что они все работают, даже для не предназначенной для них задачи.

Экспериментальная часть

Лабораторная работа №1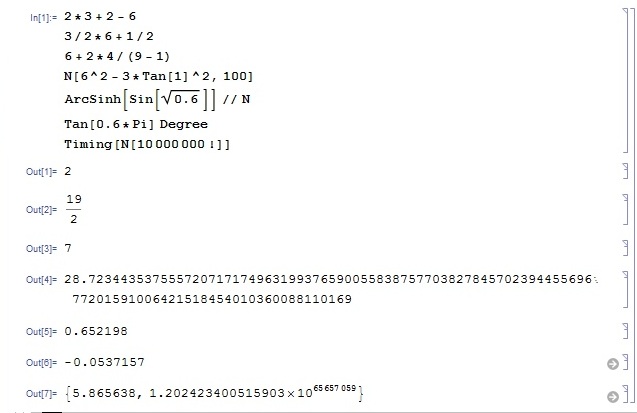

Лабораторная работа №2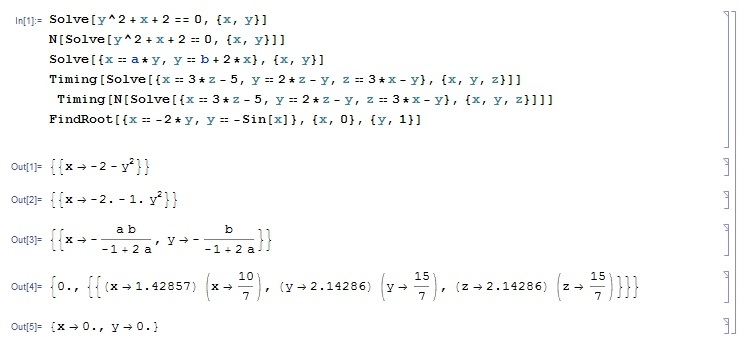

Лабораторная работа №3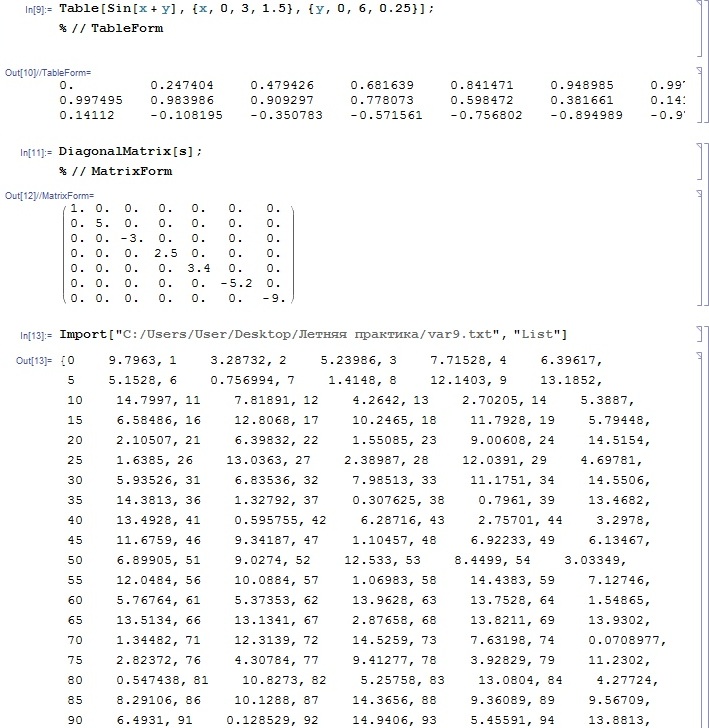

Лабораторная работа №4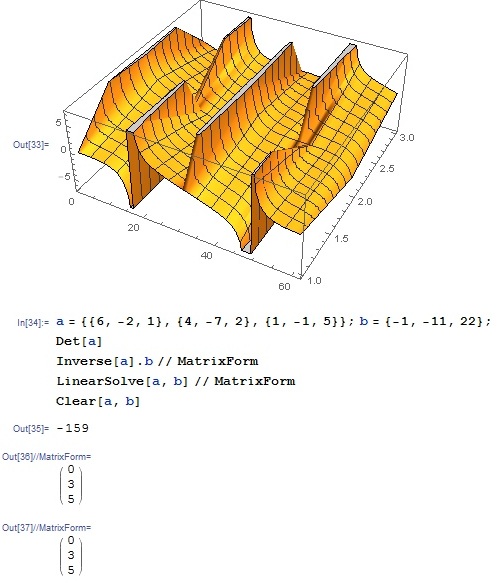

Лабораторная работа №5

Лабораторная работа №6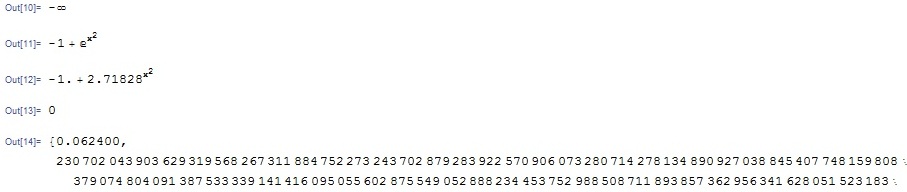

Лабораторная работа №7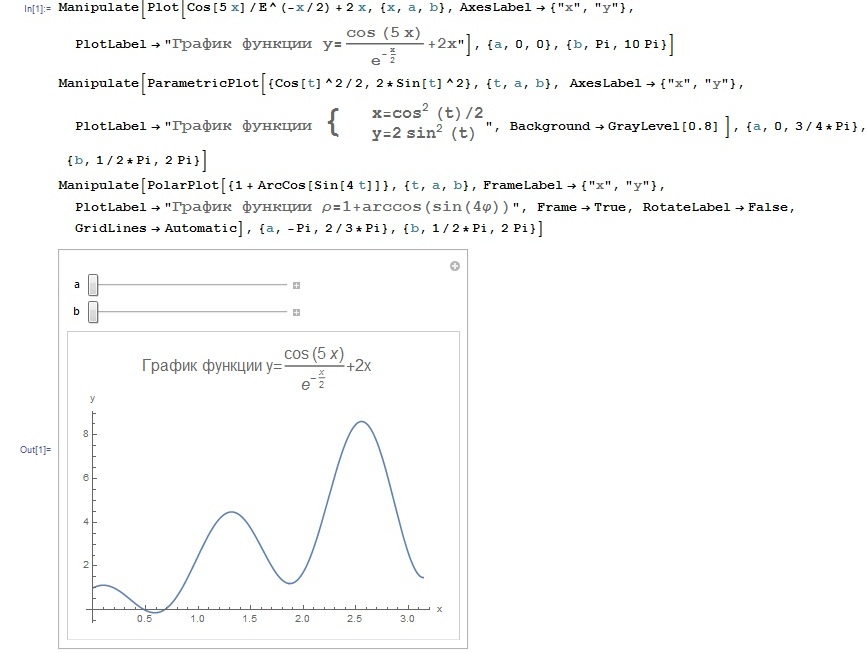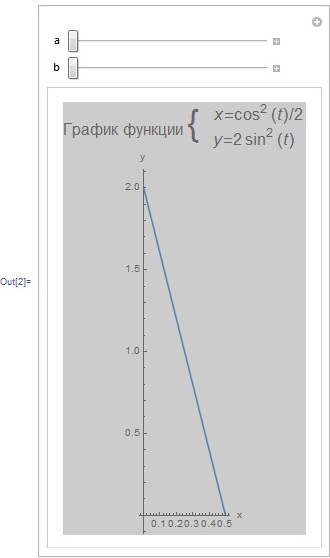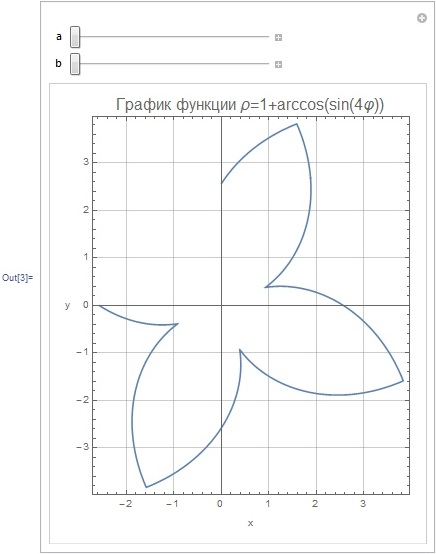

Лабораторная работа №8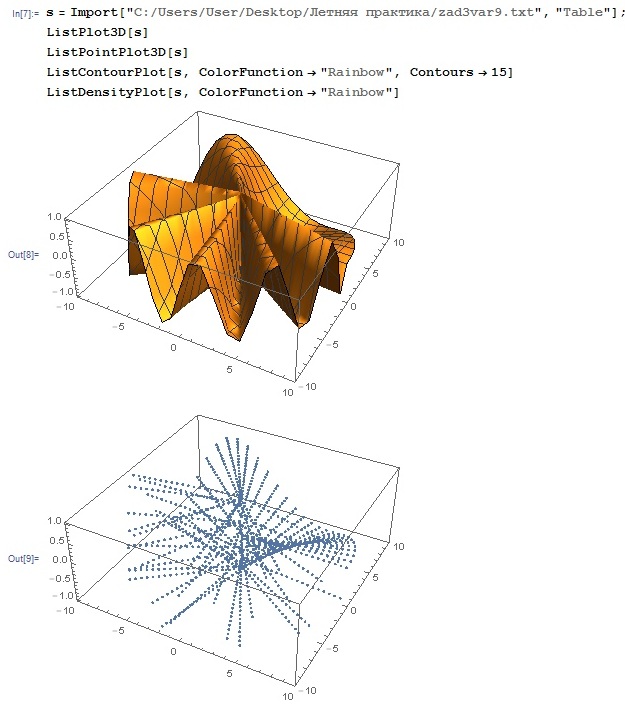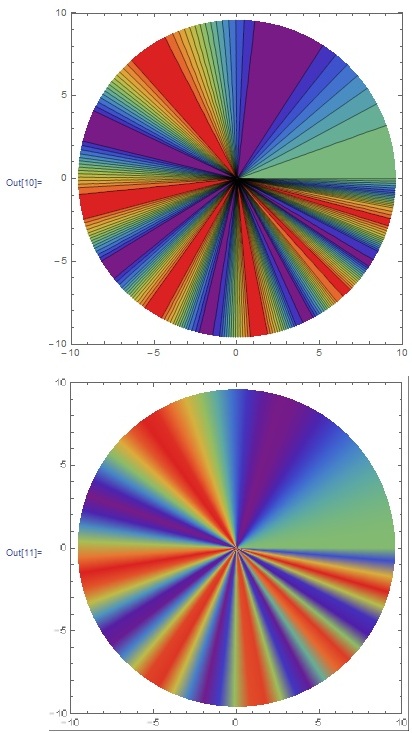

Лабораторная работа №9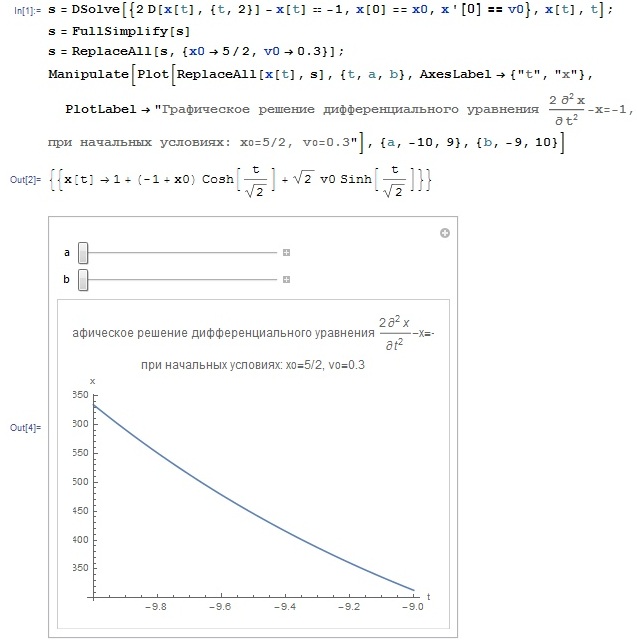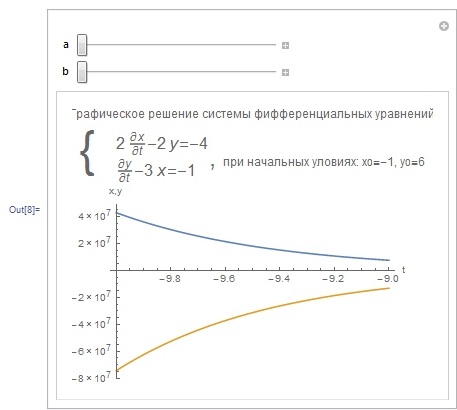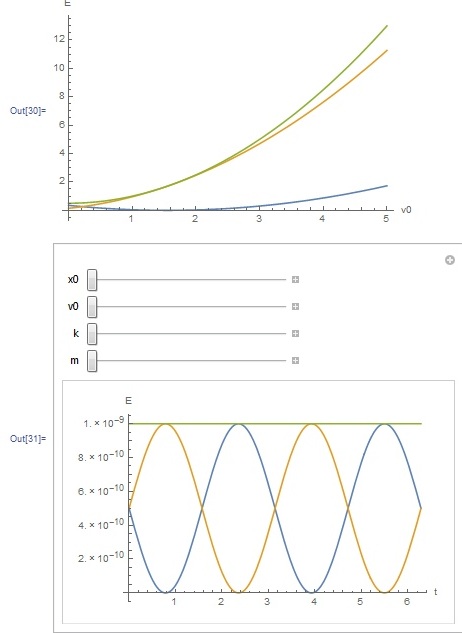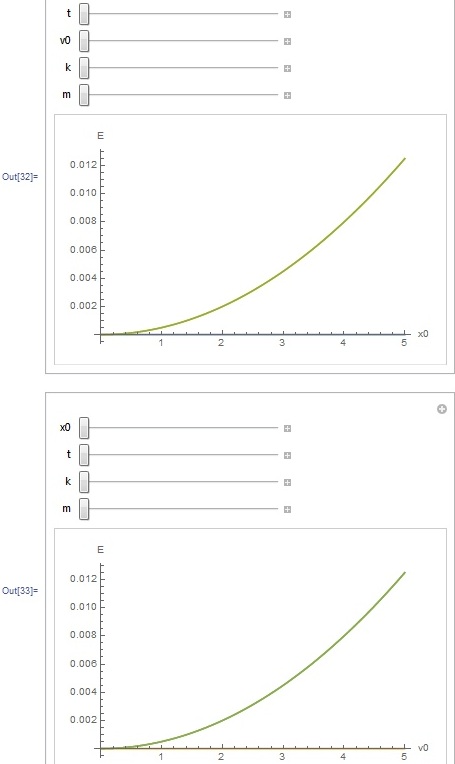

Лабораторная работа №10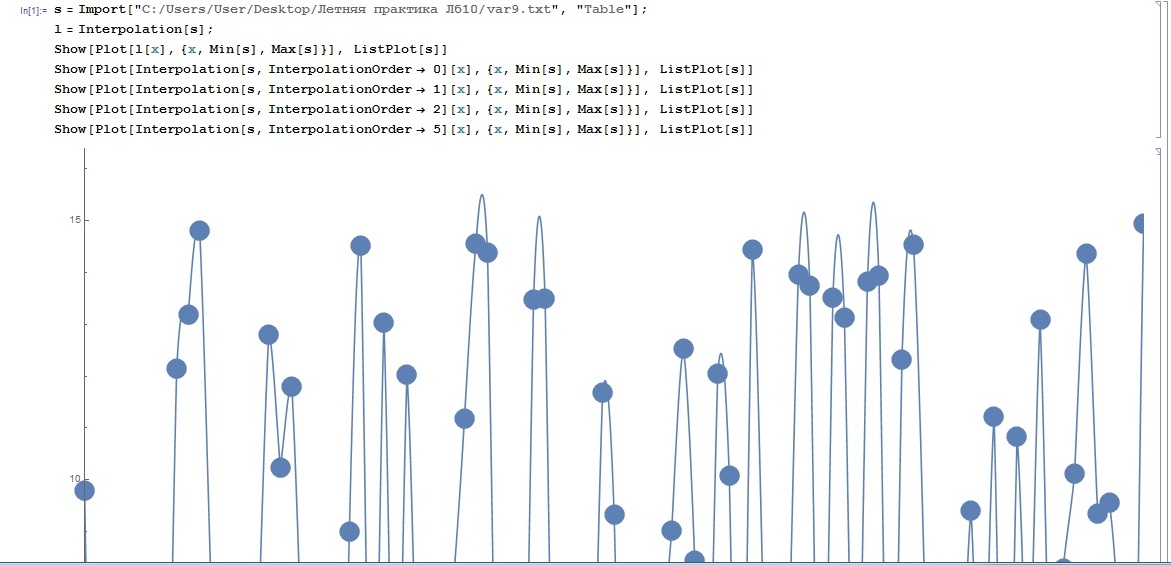

Заключение

В результате прохождения летней практики были получены навыки работы в пакете Mathematica. Он был использован как мощный калькулятор, с его помощью были решены как простые, так и сложные уравнения, и системы линейных, трансцендентных и дифференциальных уравнений. Были освоены функции математического анализа и построения функций, заданных различными способами. Также были рассмотрены динамические функции, позволяющие изменять ответ, меняя переменные различными способами. Самым трудным заданием было использование динамических функций, которые не были описаны в методических пособиях. Их синтаксис изучался, в основном, методом проб и ошибок и из встроенной справки. В общем же, синтаксис всех функций интуитивно понятен. Также, по сравнению с языками программирования, в пакете Mathematica существует огромное количество различных функций для различных задач. То есть для того чтобы перемножить две матрицы в таких языках программирования как C++ или Delphi требуется написать программу для этих вычислений или подгружать дополнительные библиотеки, а в пакете Mathematica существует специальная функция для этих вычислений, и так со многими математическими вычислениями.