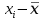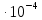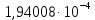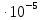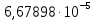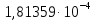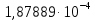Обработка и формы представления результата прямых измерений с многократными наблюдениями. Отчет по практической работе 1 Вариант 25 по дисциплине Метрология, стандартизация и сертификация
 Скачать 87.95 Kb. Скачать 87.95 Kb.
|
Вычисление среднего арифметического исправленных результатов наблюденийЗа результат измерений (оценку измеряемой величины) принимают среднее арифметическое результатов наблюдения: 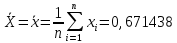 B BВычисление среднего квадратического отклоненияДля расчета среднего квадратического отклонения результатов измерений и смещенной оценки среднего квадратического отклонения можно воспользоваться данными из таблицы 2. Тогда:  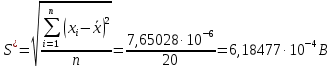  Среднее квадратическое отклонение среднего арифметического (оценки измеряемой величины) можно найти из среднего квадратического отклонения результатов измерений: Среднее квадратическое отклонение среднего арифметического (оценки измеряемой величины) можно найти из среднего квадратического отклонения результатов измерений: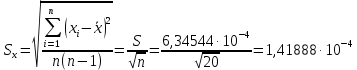 Проверка гипотезы о том, что результаты наблюдений принадлежат нормальному распределению Согласно ГОСТ 8.736-2011 при числе результатов измерений 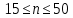 нормальность их распределения проверяют с помощью составного критерия. Исследование будет проводиться в 2 этапа: проверка гипотезы о том, что результаты наблюдений принадлежат нормальному распределению по критерию А; проверка гипотезы о том, что результаты наблюдений принадлежат нормальному распределению по критерию Б. нормальность их распределения проверяют с помощью составного критерия. Исследование будет проводиться в 2 этапа: проверка гипотезы о том, что результаты наблюдений принадлежат нормальному распределению по критерию А; проверка гипотезы о том, что результаты наблюдений принадлежат нормальному распределению по критерию Б. Критерий А Формирование исходных данных. Исходные данные для исследования представлены в таблице 1. Формулировка нулевой (H0) и альтернативной (H1) гипотез. Гипотеза H0— распределение результатов измерений соответствует нормальному виду; Гипотеза H1 — распределение результатов измерений не соответствует нормальному виду. Выбор вида статистической проверки гипотезы. Для проверки гипотезы о том, что результаты наблюдений принадлежат нормальному закону распределения, будет использован критерий А. Определение уровня значимости. Уровень значимости q согласно заданию равен 0,01 (1%). Вычисление критического значения выбранного статистического критерия на основе исходных данных. Согласно критерию А критическое значение определяется по формуле: 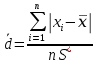 Далее, для удобства расчетов следует составить таблицу 3. Результаты промежуточных расчетов критерия А
Тогда: 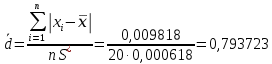 Нахождение в таблицах квантиля распределения. Согласно таблице B.1 приложения В при уровне значимости q и объеме выборки n квантили распределения 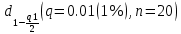 и и 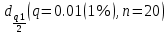 равны: равны: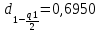 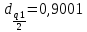 Проверка, выполняется ли указанное в выбранном критерии условие. Согласно критерию А, распределение результатов наблюдений соответствует нормальному виду, если выполняется неравенство: 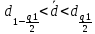 где:  И И 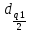 квантили распределения, получаемые из квантили распределения, получаемые из таблицы B.1 приложения В. При подстановке значений данное условие примет вид: 0,6950 < 0,793723 < 0,9001. Формулировка вывода. Видно, что условие 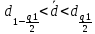 выполняется, следовательно принимается нулевая гипотеза и отвергается альтернативная гипотеза. выполняется, следовательно принимается нулевая гипотеза и отвергается альтернативная гипотеза.Вывод: условие критерия А выполняется, следовательно, отвергается альтернативная гипотеза (H1) и принимается нулевая гипотеза (H0), согласно которой распределение результатов измерений соответствует нормальному. Критерий Б Формирование исходных данных. Исходные данные для исследования представлены в таблице 1. Формулировка нулевой (H0) и альтернативной (H1) гипотез. Гипотеза H0— распределение результатов измерений соответствует нормальному; Гипотеза H1 — распределение результатов измерений не соответствует нормальному. Выбор вида статистической проверки гипотезы. Для проверки гипотезы о том, что результаты наблюдений принадлежат нормальному закону распределения, будет использован Определение уровня значимости. Уровень значимости q согласно заданию равен 0,01 (1%). Вычисление фактического значения выбранного статистического критерия на основе исходных данных. Поскольку в данном критерии расчеты и проверка связаны друг с другом, все вычисления сведены в один этап. Нахождение в таблицах квантиля распределения. Согласно таблице B.2 приложения В для числа измерений n = 20, значение параметра m равно 1, уровень доверительной вероятности Рдля уровня значимости q = 0,01 (1%) составляет 0,99. Тогда согласно таблице В.3 приложения В значение квантиля 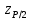 составляет: составляет: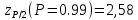 . .Проверка, выполняется ли указанное в выбранном критерии условие. Согласно критерию Б, распределение результатов наблюдений соответствует нормальному, если не более m разностей 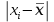 превысили значение превысили значение 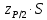 т.е. т.е.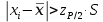 где S —среднее квадратическое отклонение; 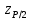 — верхняя квантиль распределения нормированной функции Лапласа, отвечающая вероятности P/2. — верхняя квантиль распределения нормированной функции Лапласа, отвечающая вероятности P/2.В данном случае: 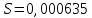  Далее, для удобства расчетов следует составить таблицу 4. Результаты промежуточных расчетов критерия Б
Как видно из таблицы 4 ни одна разность вида 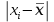 не превысила значение не превысила значение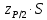 , следовательно, критическая статистика — m* = 0. , следовательно, критическая статистика — m* = 0.Формулировка вывода. Вывод: установлено, что ни одна из разностей 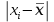 не превысила значение не превысила значение 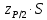 , следовательно, отвергается альтернативная гипотеза (H1) и принимается нулевая гипотеза (H0), согласно которой распределение результатов измерений соответствует нормальному. , следовательно, отвергается альтернативная гипотеза (H1) и принимается нулевая гипотеза (H0), согласно которой распределение результатов измерений соответствует нормальному.Поскольку оба критерия установили, что распределение результатов наблюдений группы соответствует нормальному виду, то формируется соответствующий вывод: вид закона распределения результатов наблюдений выборки соответствует нормальному | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||