Практические работы по метрологии. Викторов Р.В. Практическая работа №4. Отчет по практической работе 4 обработка результатов прямых многократных измерений
 Скачать 36.35 Kb. Скачать 36.35 Kb.
|
|
Министерство науки и высшего образования РФ Федеральное Государственное бюджетное образовательное учреждение высшего образования «Поволжский государсТвенный технологический университет» (ФГБОУ ВО «ПГТУ») Кафедра РТ и МБС Отчет по практической работе №4 «ОБРАБОТКА РЕЗУЛЬТАТОВ ПРЯМЫХ МНОГОКРАТНЫХ ИЗМЕРЕНИЙ» Вариант 8 Выполнил: студент группы ИТС-31з Викторов Р.В. (дата) (подпись) Проверил: к.т.н., доцент РТ и МБС Охотников С.А. (дата) (подпись) Йошкар-Ола 2020 Задание: При многократном измерении индукции магнитного поля,получен ряд измеренных значений (таблица 1). Провести обработку результатов измерений. Записать результат измерения величины 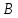 . .Таблица 1-Исходные данные
Доверительная вероятность: Р=0,95 Определяем подозрительный результат измерения: -измерение №14, 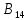 = 67 = 67 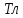 Определяем, содержит ли данное значение грубый промах. Предварительно исключаем его из ряда результатов измерений. Для удобства и быстроты вычислений расчеты будем проводить используя программный пакет Microsoft Office Excel (таблица 2). Определяем среднее арифметическое значение исправленного ряда результатов измерения: 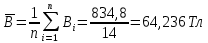 Таблица 2. Результаты расчетов.
Определяем среднее квадратическое отклонение по формуле: 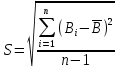 Оценка среднего квадратического отклонения: 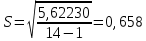 По критерию Романовского при доверительной вероятности Р=0,95 и n=14 определяем  2,617 2,617Вычисляем для подозрительного значения: 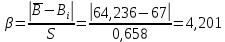 Поскольку 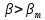 (4,201>2,617) результат (4,201>2,617) результат  = 67 = 67 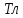 следует отбросить как содержащий грубую погрешность. следует отбросить как содержащий грубую погрешность. Вычислим среднюю квадратическую погрешность среднего арифметического: 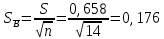 Вычисляем доверительные границы случайной составляющей погрешности результата измерения для доверительной вероятности Pд = 0,95. Считаем, что распределение результатов измерений подчиняется нормальному закону. Доверительные границы случайной погрешности измерений находят с помощью квантилей распределения (коэффициентов) Стьюдента по формулам:  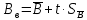 где 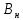 и и 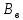 – соответственно координаты нижней и верхней границ доверительного интервала; t – квантиль распределения Стьюдента. – соответственно координаты нижней и верхней границ доверительного интервала; t – квантиль распределения Стьюдента.Число наблюдений n=14. По таблице распределения Стьюдента находим значение  , соответствующее вероятности РД=0,95: , соответствующее вероятности РД=0,95: =2,15. =2,15.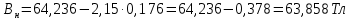  Записываем результат измерения: 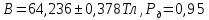 Ответы на контрольные вопросы.1. В каких случаях проводят многократные измерения? Что принимают за результат таких измерений? В результате статистической обработки результатов многократных измерений удается уменьшить влияние случайной составляющей погрешности. За результат измерения принимают среднее арифметическое результатов измерений, в которые предварительно введены поправки для исключения систематических погрешностей. 2. Дайте определение следующих понятий: доверительная вероятность, доверительная граница случайной погрешности измерения, промах. Доверительная вероятность - вероятность того, что истинное значение измеряемой величины лежит внутри некоторого интервала. Доверительные границы - наибольшее и наименьшее значения погрешности измерений, ограничивающие интервал, внутри которого с заданной вероятностью находится искомое (истинное) значение погрешности результата измерений. Промах - это случайная погрешность результата отдельного наблюдения, входящего в ряд измерений; для данных условий она резко отличается от остальных результатов этого ряда. 3. Что такое доверительный интервал? Доверительный интервал – это некоторый интервал внутри которого лежит истинное значение. 4. Назовите основные числовые характеристики ряда наблюдений. 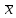 – среднее арифметическое значение исправленного ряда измерений; – среднее арифметическое значение исправленного ряда измерений;S – средняя квадратическая погрешность измерений (стандартное отклонение); 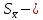 средняя квадратическая погрешность среднего арифметического. средняя квадратическая погрешность среднего арифметического.5. Чем отличается дисперсия ряда наблюдений от дисперсии результата измерений? Дисперсия ряда наблюдений характеризует степень рассеивания ( разброса) результатов отдельных наблюдений вокруг математического ожидания. Чем меньше дисперсия, тем меньше разброс отдельных результатов, тем точнее выполнены измерения. 6. Какие критерии согласия вы знаете? Для чего они служат? Критерий Романовского. При расчете S не используют подозрительный результат 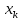 . Значение S характеризует степень рассеяния единичных результатов ряда измерений . Значение S характеризует степень рассеяния единичных результатов ряда измерений 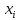 около среднего их значения. Чем больше S, тем значительнее возможное отклонение значений около среднего их значения. Чем больше S, тем значительнее возможное отклонение значений 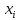 от x . Средняя квадратическая погрешность S является основной характеристикой величины случайных погрешностей результатов измерений. от x . Средняя квадратическая погрешность S является основной характеристикой величины случайных погрешностей результатов измерений. В зависимости от выбранной доверительной вероятности Р и числа измерений n из таблицы находят теоретический уровень значимости 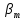 и сравнивают с ним рассчитанное значение β. Если β > и сравнивают с ним рассчитанное значение β. Если β > 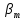 , то результат , то результат 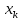 следует отбросить как содержащий грубую погрешность. Если β < следует отбросить как содержащий грубую погрешность. Если β < 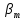 , то выборку следует сохранить в полном объёме. Как правило, критерий Романовского применяют при объёме выборки n < 20. , то выборку следует сохранить в полном объёме. Как правило, критерий Романовского применяют при объёме выборки n < 20.7. Как представить результаты измерений с многократными наблюдениями? Результаты измерений с многократными наблюдениями записывают в виде: 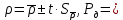 . . |