физика. Кочеткова22гк Физика1. Дисперсия света Дисперсия света
 Скачать 75.09 Kb.
|
|
Дисперсия света Дисперсия света - это явления, обусловленные зависимостью показателя преломления вещества от длины волны (или частоты): n = f (l), где l - длина волны света в вакууме. Производную dn/dl называют дисперсией вещества. Для прозрачных бесцветных веществ график зависимости n(l) в видимой части спектра имеет вид, показанный на рисунке. Интервал длин волн, в котором dn/dl < 0 (как на рисунке), соответствует нормальной дисперсии. Те же интервалы длин волн, где дисперсия вещества dn/dl > 0, соответствуют аномальной дисперсии. На рисунке показан график зависимости n(l) с участками нормальной и аномальной дисперсии. Заметим, что область аномальной дисперсии совпадает с полосой поглощения c(l). 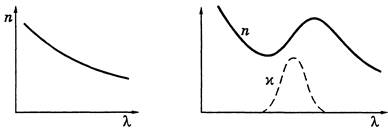 Все вещества в той или иной степени являются диспергирующими. Вакуум, как показали тщательные исследования, дисперсией не обладает. Аналитический вид зависимости n(l) в области нормальной дисперсии для не слишком больших интервалов длин волн может быть представлен приближенной формулой n = a + b/l2, где а и b положительные постоянные, значения которых для каждого вещества определяются из опыта. Классическая теория дисперсии Дисперсию света можно объяснить на основе электромагнитной теории и электронной теории вещества. Строго говоря, поведение электронов в атомах подчиняется законам квантовой физики. Однако для качественного понимания дисперсии света достаточно ограничиться классическими представлениями, которые, как это не удивительно, приводят к тем же результатам, что и квантовая теория. Поставим перед собой задачу объяснить ход зависимости n(w). Известно, что в изотропной немагнитной среде  . В свою очередь e можно найти из соотношения e = 1 + c, где c - диэлектрическая восприимчивость, которая является коэффициентом в соотношении Р = ce0Е, Р - поляризованность, т.е. дипольный момент единицы объема. таким образом: , где Рх - проекция вектора Р на ось х, вдоль которой совершаются колебания вектора Е.Известно, что Рх = n0px, где n0 - концентрация диполей, px - проекция дипольного момента отдельного диполя. В дальнейшем мы будем рассматривать простейшую модель вещества, состоящего из не взаимодействующих друг с другом атомов. Каждый атом представляет собой ядро, окруженное быстро движущимися электронами, которые в совокупности как бы «размазаны» по сферически симметричной области вокруг ядра. Поэтому принято говорить, что ядро с зарядом q окружено «электронным облаком» с зарядом (- q). В отсутствие внешнего поля Е центр электронного облака совпадает с ядром, и дипольный момент атома равен нулю. При наличии же внешнего поля Е электронное облако смещается относительно практически неподвижного ядра, и возникает дипольный момент р = ql, где q > 0, а l - вектор, проведенный из центра «облака» к ядру. Проекция вектора р на ось х равна рх = qlx = q(-x) = -qx здесь х - смещение центра «облака» из положения равновесия, т.е. относительно ядра. Заметим, что центр «облака» ведет себя как точечный заряд (-q). С учетом последнего соотношения получаем  Как видно, задача сводится к определению х(t) под действием Ех(t). Для этого запишем уравнение движения электронного облака как  , где m - масса электронного облака, а справа записаны проекции на ось х квазиупругой силы, силы «сопротивления», обусловленной чем-то вроде «трения» облака о ядро, и вынуждающей силы со стороны гармонической электромагнитной волны частоты w.Разделив уравнение на m, приведем его к виду  , где w2 = k/m, 2b = r/m, fm = qEm/m.Для теории дисперсии имеет значение не общее, а только частное (установившееся) решение уравнения x = a cos(wt - j), где а - амплитуда колебаний, j - разность фаз между смещением х и силой fmcoswt. Подстановка этого решения в дифференциальное уравнение позволяет с помощью векторной диаграммы найти значения амплитуды а и разности фаз j, а именно: 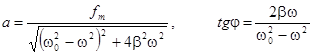 (решение уравнения подробно рассматривается в теории колебаний)Ограничимся простейшим случаем, когда  <<  , т.е. когда вынуждающая частота (поля) не очень близка к собственной частоте w0 колебаний электронного облака и коэффициент b, характеризующий затухание, достаточно мал. В этом случае, если w < w0, то Такой же результат будет и при w > w0, когда j = p. Учитывая также, что qEmcoswt = -qEx  , где b = n0q2/e0m = N0e2/e0me, N0 - концентрация электронов (здесь учтено, что q = Ze, m = Zme и N0 = Zn0, Z - число электронов в атоме).Разрыв функции e(w) при w = w0 и обращение ее в ±¥ не имеют физического смысла, это получилось вследствие игнорирования затухания (b ® 0). Если же его учесть, то ход кривой будет иным (рисунок) и достаточно хорошо подтверждается экспериментально. Зависимость c(w) характеризует полосу поглощения. Как раз с ней совпадает область аномальной дисперсии (dn/dw < 0). 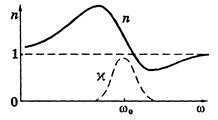 Заметим, что собственных частот w0i может быть несколько в атоме, соответственно будет и несколько областей аномальной дисперсии. Кроме того, как видно из рисунка, при w > w0 показатель преломления (n =  ) , будет меньше единицы, а это значит, что фазовая скорость электромагнитной волны v = c/n оказывается больше с! Подобное имеет место в плазме, где w0 = 0 (электроны свободные), и для рентгеновского излучения (w > w0). Никакого противоречия с теорией относительности здесь нет. Последняя утверждает, что скорость сигнала (импульса) не может превышать с. Понятие же показателя преломления применимо к монохроматическим электромагнитным волнам, бесконечным в пространстве и во времени. Такие волны не могут служить для передачи сигнала, а, кроме того, их в принципе невозможно осуществить.Из выражения  вытекает и еще одно неожиданное следствие для случая, когда w0 = 0 (например, в той же плазме). При этом условии, когда частота электромагнитной волны w  , оказывается, что диэлектрическая проницаемость e(w)£ 0, а следовательно, показатель преломления для таких частот становится мнимым, и его можно представить как n = ic. Выясним, что это означает.Запишем уравнение электромагнитной волны в комплексной форме:  , где k = 2p/l, где l - длина волны в среде. Если длина волны в вакууме l0, то l = l0/n, и где k0 = 2p/l0 и n = ic Подставив выражение для k в исходное уравнение волны, получим: E = E0 exp(-ck0x)  или для действительной части E = E0 exp(-ck0x) coswt Видно, что в рассматриваемом случае мы имеем стоячую волну, амплитуда которой экспоненциально затухает. Фактически это означает, что излучение при e £ 0 не может пройти через плазму и происходит его полное отражение его в пограничном слое. Групповая скорость Волновой пакет Строго монохроматическая волна это идеализация. Любая реальная волна, согласно теореме Фурье, может быть представлена как суперпозиция монохроматических волн с различными амплитудами и частотами w в некотором интервале Dw. Суперпозицию волн, мало отличающихся друг от друга по частотам (Dw << w), называют волновым пакетом или группой волн. Вид волнового пакета в некоторый момент времени показан на рисунке. В его пределах монохроматические составляющие усиливают друг друга, вне пакета практически гасят друг друга. 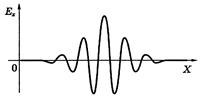 В вакууме все монохроматические волны, образующие пакет, распространяются с одинаковой фазовой скоростью v = w/k, где k - волновое число (2p/l). С такой же скоростью распространяется в вакууме и сам волновой пакет, не изменяя своей формы. Групповая скорость В диспергирующей среде волновой пакет расплывается, поскольку скорости его монохроматических составляющих отличаются друг от друга, и понятие скорости такой волны требует уточнения. Если дисперсия достаточно мала, расплывание волнового пакета происходит не слишком быстро. В этом случае волновому пакету можно приписать скорость u, с которой перемещается его «центр тяжести». Это так называемая групповая скорость. Соответствующий расчет дает, что групповая скорость определяется как u = dw/dk Поясним эту формулу на примере суперпозиции двух волн с одинаковой амплитудой и несколько отличными друг от друга длинами волн (и частотами). На рисунке показано их относительное расположение (а) в некоторый момент времени, а также результат их суперпозиции (б). Нас будет интересовать скорость, с которой перемещается место с максимальной амплитудой - это и будет скорость волнового пакета - групповая скорость. Определим ее величину.  Пусть уравнения этих двух монохроматических волн имеют вид: E1 = A cos(wt - kx), E2 = A cos[(w + dw)t - (k + dk)x] В результате их наложения образуется суммарная волна E = E1 + E2 =2A cos  cos (wt - kx)Это выражение можно рассматривать как уравнение монохроматической волны, амплитуда которой меняется по закону  Отсюда следует, что точки, соответствующие, например, максимуму амплитуды, движутся по закону tdw - xdk = 0, откуда х = (dw/dk)t Величина в скобках и есть групповая скорость. Выражение для групповой скорости можно представить в ином виде. Заменив w через vk, получим:  Так как k = 2p/l dk = - (2p/l2)dl, где l - длина волны в среде, то выражение для u можно переписать так:  Это так называемая формула Рэлея. В области нормальной дисперсии (dv/dl > 0) групповая скорость совпадает с фазовой. Существует простой графический способ нахождения групповой скорости по кривой v(l). Он показан на рисунке. В случае группы волн роль играет только малый участок кривой v(l) в узком диапазоне Dl (Dl << l). отрезок, который отсекает на оси ординат касательная к кривой v(l), проведенная через точку А, равен v - l (dv/dl), т.е. групповой скорости u при данной длине волны l. 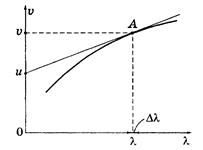 Следует отметить, что в области аномальной дисперсии импульс сильно деформируется, и групповая скорость в таких условиях теряет определенное физическое содержание. Рассмотрим вопрос о скорости распространения энергии, переносимой электромагнитной волной. Прежде всего, заметим, что фазовая скорость монохроматической волны не имеет ничего общего со скоростью переноса энергии. Фазовая скорость устанавливает только связь между фазами колебаний в различных точках пространства. Строго монохроматическая волна не может служить для передачи сигнала, поскольку она не имеет ни начала, ни конца во времени и пространстве. Поэтому распространение сигнала связано с перемещением изменений амплитуды. И в тех случаях, когда групповая скорость имеет смысл (т.е. электромагнитный импульс распространяется не расплываясь), она совпадает со скоростью переноса энергии. Прямые измерения скорости света сводятся к измерению расстояния, проходимого световым сигналом (импульсом) за определенный промежуток времени. Этот метод практически дает групповую скорость. То же самое, как показывает подробный анализ, относится ко всем известным косвенным методам измерения скорости света. Фазовую же скорость (точнее отношение фазовых скоростей в двух различных средах) можно определить по отношению показателей преломления, или воспользовавшись законом преломления. Поглощение света Закон Бугера Прохождение световой волны через вещество сопровождается потерей энергии этой волны, затрачиваемой на возбуждение колебаний электронов (точнее на изменение их состояния в атоме). Частично эта энергия возвращается излучению в виде вторичных волн, порождаемых колеблющимися электронами; частично же она переходит в другие формы энергии ( во внутреннюю энергию вещества). Поэтому интенсивность света при прохождении через вещество уменьшается - свет поглощается в веществе. Поглощение света можно описать с энергетической точки зрения, не вникая в механизм взаимодействия света с атомами вещества, чем мы и воспользуемся. Пусть через однородное вещество распространяется параллельный световой пучок. Выделим мысленно в этом веществе бесконечно тонкий плоский слой толщины dx (рисунок). Ясно, что эта величина будет пропорциональна интенсивности в данном поглощающем слое и его толщине dx, т.е. -dI = cIdx, где c - коэффициент поглощения, он характеризует поглощающие свойства вещества. Разделив переменные, получим: -dI/I = cdx. После интегрирования в пределах от I0 до I и от 0 до х найдем: ln(I/I0) = -cx, откуда  Это и есть закон Бугера. Таким образом, интенсивность света при прохождении однородного вещества уменьшается по экспоненциальному закону. 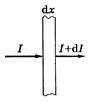 О коэффициентах поглощения Для всех веществ поглощение имеет селективный характер, т.е. коэффициент поглощения c зависит от длины волны света (в вакууме). Для жидких и твердых веществ зависимость c(l) имеет вид, подобный изображенному на рисунке. Т.е. сильное поглощение обнаруживается в достаточно широком интервале длин волн. 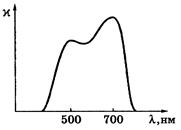 Совсем иначе ведет себя коэффициент c(l) в случае газов или паров металлов при невысоком давлении. Здесь для всех длин волн коэффициент поглощения практически равен нулю, и лишь для очень узких спектральных интервалов dl (порядка нескольких тысячных нм) обнаруживает резкие максимумы (рисунок). Эти максимумы соответствуют резонансным частотам колебаний электронов внутри атомов, которые практически не взаимодействуют друг с другом. 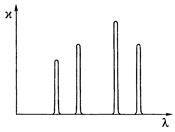 При повышении же давления максимумы поглощения все больше расширяются, и при высоких давлениях спектр c(l) приближается к спектрам поглощения жидкостей. Это связано с ростом взаимодействия между атомами. |