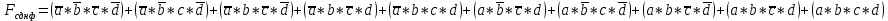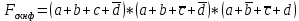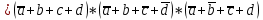инфа отчет. Отчет 5 практическая. Отчет по практической работе 5 Построение комбинационных схем, реализующих сднф и скнф заданной логической функции от 4х переменных по дисциплине

• Название: Отчет по практической работе 5 Построение комбинационных схем, реализующих сднф и скнф заданной логической функции от 4х переменных по дисциплине
• Анкор: инфа отчет
• Дата: 21.11.2022
• Размер: 259.13 Kb.
• Имя файла: Отчет 5 практическая.docx
• Тип: Отчет; #803688

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение высшего

образования

«МИРЭА - Российский технологический университет»
РТУ МИРЭА




Институт искусственного интеллекта

Кафедра общей информатики

ОТЧЕТ

ПО ПРАКТИЧЕСКОЙ РАБОТЕ № 5

Построение комбинационных схем, реализующих СДНФ и СКНФ заданной логической функции от 4-х переменных

по дисциплине

«ИНФОРМАТИКА»

Выполнил студент группы ИВБО-04-22 Немцов Д.Д.

Принял Корчемная А.И.

Ассистент

Практическая	«7» октября 2022 г.	__________________
работа выполнена
«Зачтено»	«»2022 г.	__________________

Москва 2022

СОДЕРЖАНИЕ

ОТЧЕТ 1

по дисциплине 1

1ПОСТАНОВКА ЗАДАЧИ 3

2ПРОЕКТИРОВАНИЕ И РЕАЛИЗАЦИЯ 4

2.1Восстановленная таблица истинности 4

2.2Формулы СДНФ и СКНФ 5

2.3Схемы, реализующие СДНФ и СКНФ в общем логическом базисе 5

3ВЫВОДЫ 7

4ИНФОРМАЦИОННЫЕ ИСТОЧНИКИ 8

1 ПОСТАНОВКА ЗАДАЧИ 3

2 ПРОЕКТИРОВАНИЕ И РЕАЛИЗАЦИЯ 4

2.1 Восстановленная таблица истинности 4

2.2 Формулы СДНФ и СКНФ 5

2.3 Схемы, реализующие СДНФ и СКНФ в общем логическом базисе 5

3 ВЫВОДЫ 7

4 ИНФОРМАЦИОННЫЕ ИСТОЧНИКИ 8

1. ПОСТАНОВКА ЗАДАЧИ

Логическая функция от четырёх переменных задана в 16-теричной

векторной форме. Восстановить таблицу истинности. Записать формулы СДНФ и СКНФ. Построить комбинационные схемы СДНФ и СКНФ в лабораторном комплексе, используя общий логический базис. Протестировать работу схем и убедиться в правильности. Подготовить отчёт о проделанной работе и защитить её.
F1: AD6D₁₆ = 1010 1101 0110 1101₂

2. ПРОЕКТИРОВАНИЕ И РЕАЛИЗАЦИЯ

   1. Восстановленная таблица истинности

В соответствии с вариантом функция, заданная в 16-теричной форме имеет следующий вид:

F (a, b, c, d) = AD6D₁₆

Преобразовав данную логическую функцию в двоичную запись: 1010 1101 0110 1101₂ – получается столбец значений логической функции, который необходим для восстановления полной таблицы истинности (см. табл. 1)

Таблица 1 – Таблица истинности для функции F

a	b	c	d	F
0	0	0	0	1
0	0	0	1	0
0	0	1	0	1
0	0	1	1	0
0	1	0	0	1
0	1	0	1	1
0	1	1	0	0
0	1	1	1	1
1	0	0	0	0
1	0	0	1	1
1	0	1	0	1
1	0	1	1	0
1	1	0	0	1
1	1	0	1	1
1	1	1	0	0
1	1	1	1	1

2. Формулы СДНФ и СКНФ

По восстановленной таблице истинности (см. табл. 1) записываются формулы СДНФ и СКНФ.

Для построения формулы СДНФ нужно рассмотреть наборы значений переменных, на которых функция равна единице. Переменные, равные нулю, берутся с отрицанием, а переменные, равные единице, без отрицания. В результате получается множество совершенных конъюнкций, объединив которые через дизъюнкцию образуют формулу СДНФ (см. формулу 1)

(1)

Для построения формулы СКНФ нужно рассмотреть наборы значений переменных, на которых функция равна нулю. Переменные, равные нулю, берутся без отрицания, а переменные, равные единице, с отрицанием. В результате чего получается множество совершенных дизъюнкций, объединив которые через конъюнкцию образуют формулу СКНФ (см. формулу 2)

(2)

3. Схемы, реализующие СДНФ и СКНФ в общем логическом базисе

Следующий шаг практической работы - построение в лабораторном комплексе комбинационных схем, реализующих СДНФ и СКНФ рассматриваемой функции в общем логическом базисе, тестирование их работы и убеждение в их правильности (рис. 1, 2).

На схеме СДНФ (рис. 1) в целях размещения всей схемы в пределах одного экрана объединяющая дизъюнкция разбита на две части. Аналогично была разбита объединяющая конъюнкция на рис. 2.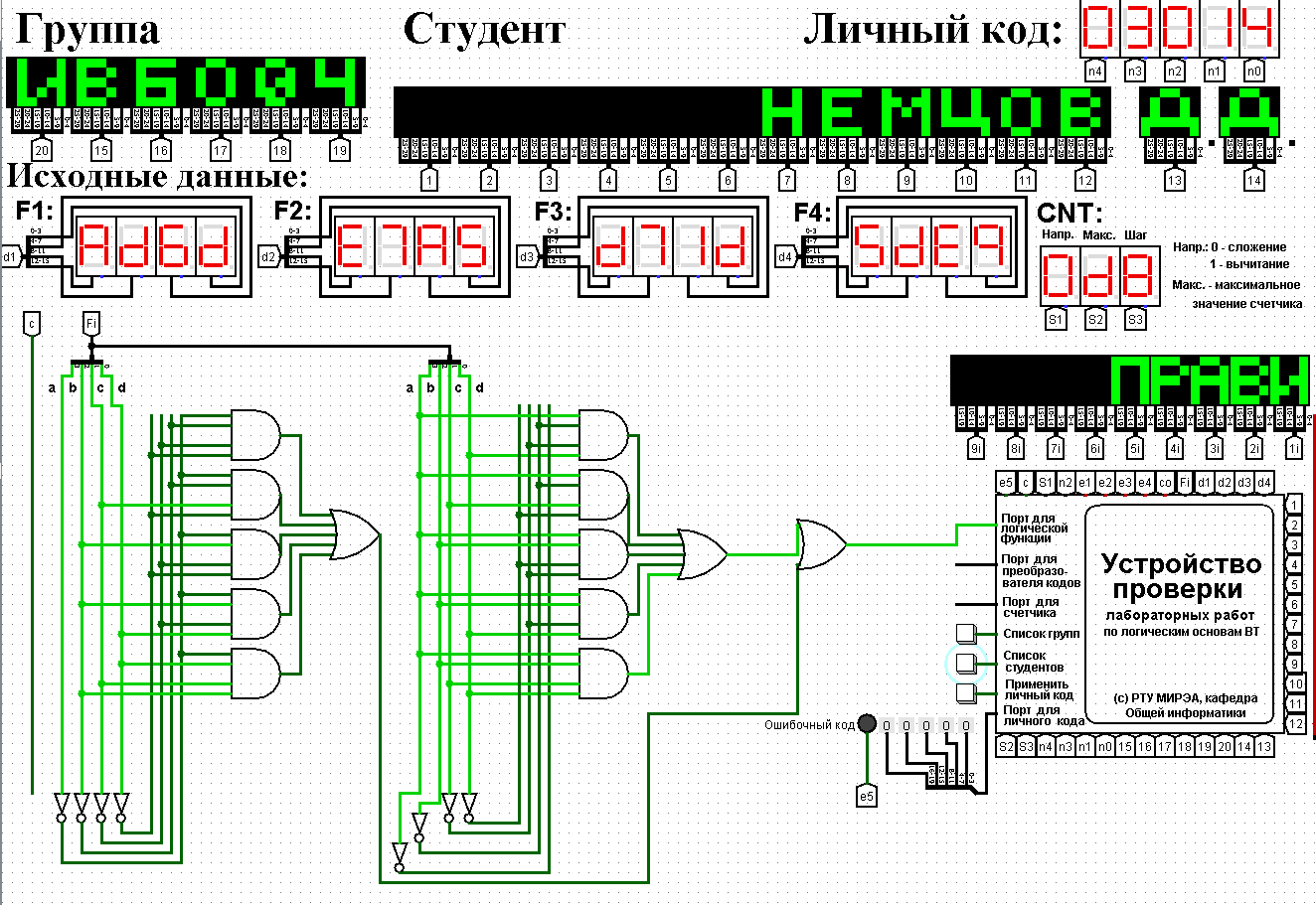



Рисунок 1 – Схема СДНФ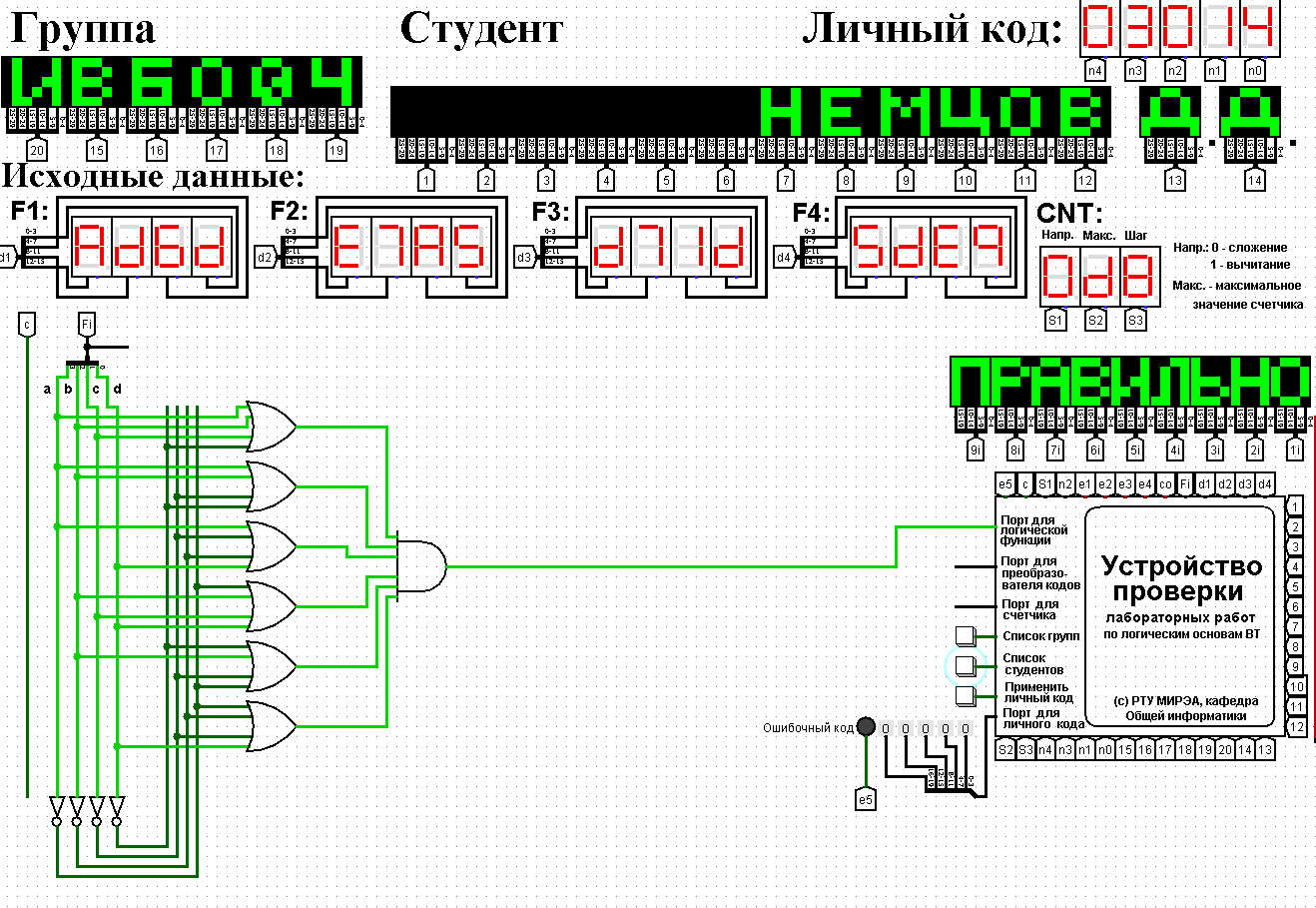



Рисунок 2 – Схема СКНФ

Тестирование показало, что все схемы работают правильно.

3. ВЫВОДЫ

По данной логической функции от четырех переменных, заданной в 16-теричной векторной форме, была восстановлена таблица истинности. По ней были составлены формула для СДНФ и формула для СКНФ. Построены комбинационные схемы СДНФ и СКНФ в лабораторном комплексе с использованием общего логического базиса. Протестирована работа схем и их правильность.

4. ИНФОРМАЦИОННЫЕ ИСТОЧНИКИ

1. 
   Информатика: Методические указания по выполнению практических и лабораторных работ / С.С. Смирнов, Д.А. Карпов; Федеральное государственное бюджетное образовательное учреждение высшего образования «МИРЭА - Российский технологический университет». – Москва: РТУ МИРЭА, 2020. – 102 с. – Текст: непосредственный.
   
2. 
   Лекции по информатике. Г.Б. Воронов — Москва: РТУ МИРЭА, 2022