отчет по 1 заданию. Отчет по практической работе Предмет Метеорологические процессы в городах и промышленных зонах

• Название: Отчет по практической работе Предмет Метеорологические процессы в городах и промышленных зонах
• Дата: 09.11.2022
• Размер: 1.63 Mb.
• Имя файла: отчет по 1 заданию.docx
• Тип: Отчет; #778704

Отчет

по практической работе

Предмет: «Метеорологические процессы в городах и промышленных зонах»

1. 
   Титульный лист
   

РГГМУ

Кафедра МКОА

Практическая работа

по курсу «Метеорологические процессы в городах и промышленных зонах» на тему: «Статистическая обработка результатов измерения

концентрации загрязняющих веществ по наблюдениям

на автоматизированных постах системы городского мониторинга» ^{Вариант № 1, NO}2

Выполнил: ст. гр. ,,,,,,,, Студент: ,,,,,,

Проверил: Мханна Ааед Исмаил Назир
СПб,2022

2. 
   Описание работы
   

Цель: проанализировать временной ряд значений концентрации диоксида азота (окиси углерода).

Задачи:

1. 
   Проверить ряд на презентабельность.
   
2. 
   Получить эмпирический закон распределения значений концентрации исследуемой величины и сравнить его с логарифмически нормальным законом распределения.
   
3. 
   Получить осредненный суточный ход исследуемой величины.
   

Исходныеданные: временной ряд значений с шагом по времени около 20 минут.

<sup>Максимально-разовая ПДК 1,1 мг/м3

Среднесуточная ПДК: 0,9 мг/м3</sup>

1. 
   Анализряда
   

ОТБРАКОВКА ДАННЫХ

Визуальная оценка ряда.

Строим график и выделяем выпадающие из общего ряда значения. Удаляем строки с отсутствующими значениями концентрации и нулевые значения.

Исходных значений 6405

После удаления пустых ячеек остается 6332, нулевые значения 6325.

Строим графики дневные, месячные и общий для того, чтобы отсечь выпадающие значения.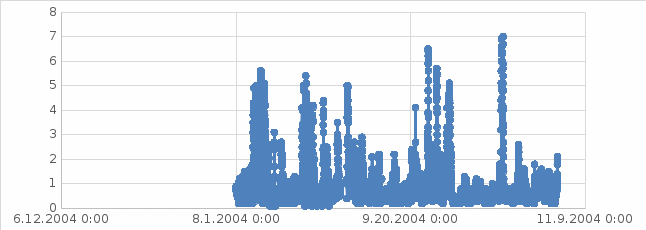

Рис.1. График изменчивости концентрации за весь период наблюдений

Таблица 1.1. Число недостоверных данных

	Число наблюдений	Период (если больше суток)
Отрицательные и нулевые значения	80	-
Отбракованные периоды	8	-
Число отбракованных наблюдений по другим причинам (если есть, с указанием причины)	-	-
Всего отбраковано наблюдений:	88	-

Таким образом, отбраковано 88 наблюдений.

ТИПИЗАЦИЯ СУТОЧНОГО ХОДА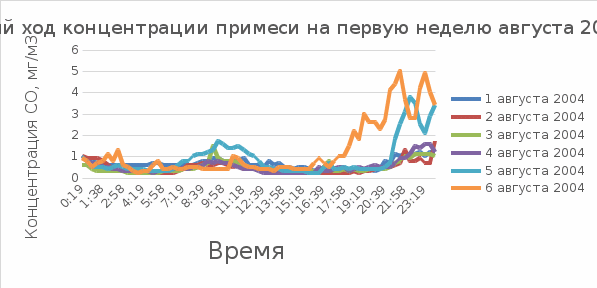

Рис.2. Суточный ход

Вывод:

На рисунке 2 приведен суточных ход концентрации СО для первой недели августа 2004 года. Видно, что в рабочие дни ход концентрации имеет общую форму, с максимумом в утренний час пик движения автотранспорта, 7:30 – 9:30 утра, и вечерний максимум, начинающийся с 20-21 часа. Днем наблюдаются низкие значения концентрации.

Выделяются графики 5 и 6 августа. Первый (5 августа) имеет пик около 21 ч.вечера и может быть связан как с метеорологическими факторами, так и с подготовкой к проведению праздничных мероприятий ко дню города. 6 августа – ярко выраженный вечерний пик, предположительно вызван автомобильным затором.

Предварительный анализ суточного хода показал наличие устойчивого суточного хода с двумя максимумами, приходящимися на пик движения автотранспорта.


Таблица 1.2. Статистические характеристики фильтрованного ряда

	Весь ряд	Месяц 1	Месяц 2	Месяц 3
Среднее значение, мг/м3	0,87	0,98	0,90	0,74
Среднеквадратичное отклонение (оно же – стандартное отклонение), мг/м3	0,91	0,82	0,82	0,77
Длина ряда, шт.	6315	2122	2084	2109
Число наблюдений, превышающих ПДК (Какое из ПДК, решите сами; будьте готовы объяснить, почему вы взяли среднесуточную ПДК, а не максимально разовую или наоборот))	1199	521	453	225
Всего значений	6315	2122	2084	2109

Проанализируем таблицу и рисунки:

• 
  процент отбраковки 1,4%;
  
• 
  общая изменчивость ряда порядка 70%;
  
• 
  превышение ПДК есть закономерность;
  
• 
  среднее значение относительно ПДК 0,87 мг/м3
  

По таблице 1.2 делаем вывод, что значительные расхождения в среднем значении концентрации и СКО отсутствуют, детального анализа не требуется.

По замечаниям выполнены графики среднего значения по месяцам и стандартного отклонения (лист «стат хар ряда» в экселе)

2. 
   Законраспределения
   

Случайной величиной называется величина, которая в результате опыта может принять то или иное значение, неизвестно заранее какое именно.
Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.


число значений
Закон распределения прерывной случайной величины Х может быть задан в следующих формах:

• 
  табличной;
  
• 
  аналитической;
  
• 
  графической.
  

Простейшей формой задания закона распределения прерывной случайной величины Х является таблица.
^xi ^x1 ^x2 ^{… x}n ^pi ^p1 ^p2 ^{… p}n
Такую таблицу называют рядом распределения случайной величины Х.
Чтобы придать ряду распределения более наглядный вид, часто прибегают к его графическому изображению¹ - гистограмме.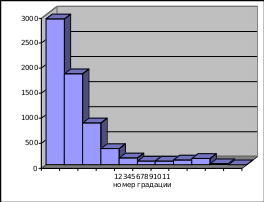

Рис.2.1. Гистограмма распределения (она же – эмпирическая плотность вероятности) По виду должна напоминать логнормальное распределение (если только повезло, и не попался пример с двухмодальным); для этого шаг при расчете гистограммы должен быть не равномерным: уменьшить в окрестности моды, увеличить на «хвостах»; всего 10-15 градаций (не больше!)

Гистограмма — способ графического представления табличных данных. Количественные соотношения некоторого показателя представлены в виде прямоугольников, площади которых пропорциональны. Чаще всего для удобства восприятия ширину прямоугольников берут одинаковую, при этом их высота определяет соотношения отображаемого параметра.

Таким образом, гистограмма представляет собой графическое изображение зависимости частоты попадания элементов выборки от соответствующего интервала группировки.<sup>2


1</sup> Случайныевеличиныизаконыихраспределения

В нашем случае гистограмма может быть построена как по количеству попаданий в диапазон, так и по вероятности попадания.
Построение гистограммы
Определяем максимальное, Qmax, и минимальное, Qmin, значения. Логично было бы их определить еще на этапе таблицы 1.2. При расчете гистограммы (особенно для NOx) можно принять Qmin=0.

Выбираете число градаций Ngrad.

Q max- Q min

Рассчитываем шаг Δq =

.

Ngrad

Концентрация в генеральной совокупности является непрерывной величиной – она может принять любое значение. Но поскольку у нас есть только выборка – измерения за конечный отрезок времени, то для нас концентрация – дискретная случайная величина. И нашей задачей является как раз перейти от табличной (дискретной) формы представления к непрерывной, от диапазона – к точке.
РАСЧЕТ ФУНКЦИЙ

1. 
   Из таблицы гистограммы получаем плотность распределения по формуле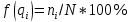
   

где n_i

– попаданий значений в диапазон, N – всего значений. Первая точка f(q) =0,

остальные расчетные.

2. 
   Рассчитываем функцию распределения как
   

F(q_i ) =

при m=0 F(q) =0, далее нарастающая сумма по f(q)

3. 
   Рассчитываем функцию обеспеченности
   

P(q) = 100 - F(q).

4. 
   Для построения графиков рассчитаем середину интервалов, по которым считалась гистограмма.
   
5. 
   Построим графики как точечную диаграмму.
   

Рис. 2.1 Расчет функций
По оси ординат – вероятность в процентах, по оси абсцисс – значения концентрации Построены кривые: 1) плотности вероятности,2) функции распределения, 3) функции обеспеченности.
Плотность вероятности и функция обеспеченности с увеличением концентрации снижается, функция распределения возрастает от 0 до 100% .

ПРОЦЕНТИЛИ

Используем функцию ПЕРСЕНТИЛЬ

Таблица 2.1.
Процентильные значения

Обеспеченность, %	Месяц 1	Месяц 2	Месяц 3
1	1,093264	1,094964	1,093839
2	2,092322	2,094005	2,092891
5	5,089496	5,091127	5,090047
10	10,08479	10,08633	10,08531

Выводы:

• 
  полученное распределение похоже на логарифмическое;
  
• 
  вероятность превышения ПДК составляет 90%;
  
• 
  Процентильные значения ежемесячно практически одинаковые.
  

3. 
   Осредненныйуточныйходдлякаждого месяцаиповсемуряду.
   

Из первого столбца с датой вытащим месяц и час с помощью функций «МЕСЯЦ» и «ЧАС» соответственно.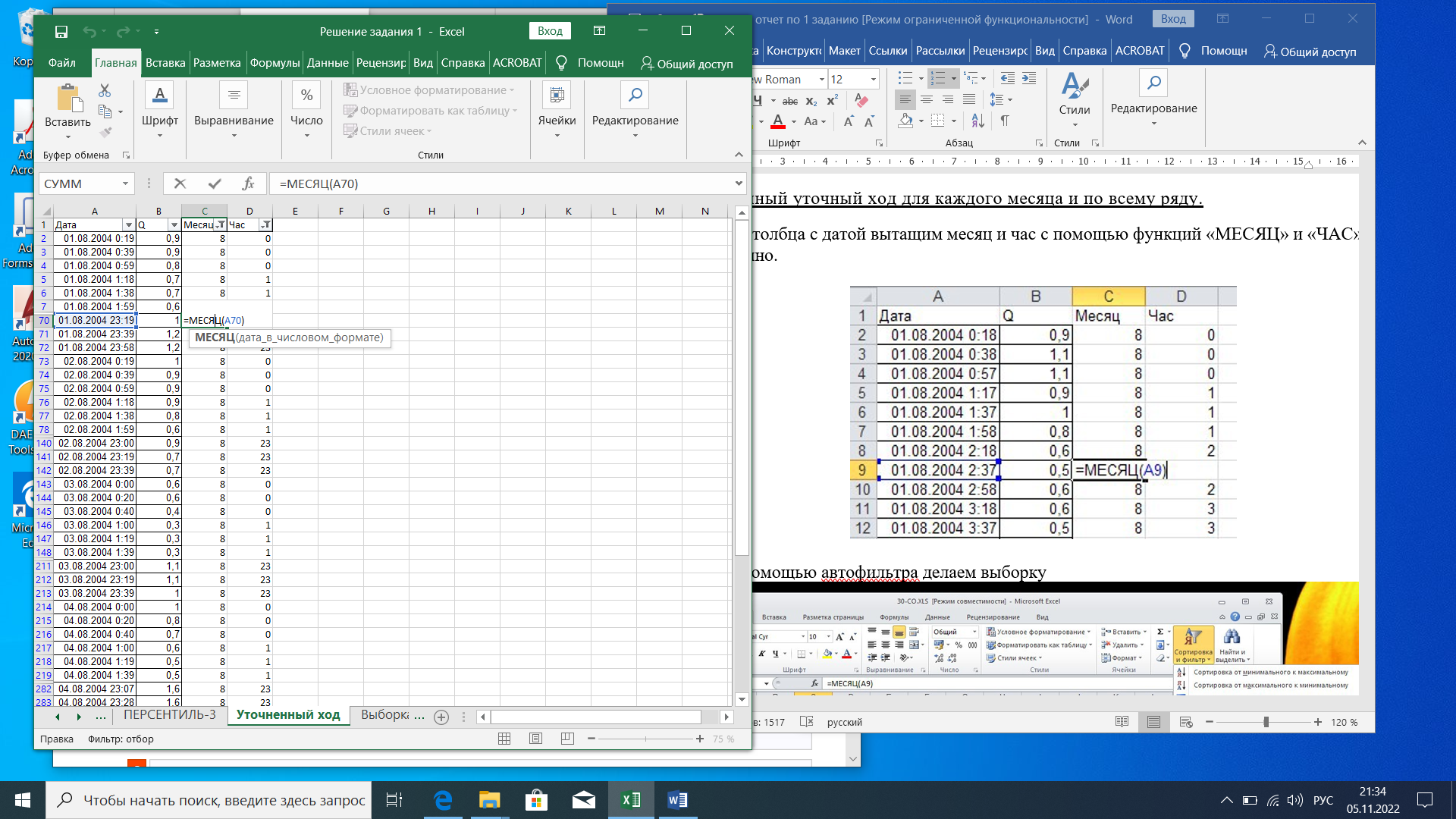

С помощью автофильтра делаем выборку по месяцам и по часам


Далее (пользователям версий 2007/2010) включаете в фильтре «Месяц» отображение каждого месяца по очереди (оставляете одну галочку), в фильтре «Час» - оставляете часы, соответствующие нужному временному диапазону.

чтоб получить среднее для 0 часов выбираем 23,0,1.

Полученную выборку (месяц-часы) копируем на отдельный лист (выборка), по столбцу Q считаем среднее и СКО. И так повторяем (3 месяца * 8 сроков) = 24 раза (24 листа в файле от 1 до 24).

Результаты расчетов заносим в таблицу 3.1
Таблица 3.1. Осредненный суточный ход исследуемой величины

1 месяц

Часы (центральные диапазона)	0	3	6	9	12	15	18	21
Среднее значение, мг/м3	1,66	1,25	1,09	1,17	0,56	0,39	0,49	1,31
СКО, мг/м3	1,53	1,43	1,11	0,8	0,29	0,23	0,35	1,19

Осредненный суточный ход исследуемой величины

2 месяц

Часы (центральные диапазона)	0	3	6	9	12	15	18	21
Среднее значение, мг/м3	1,25	0,67	0,51	1,1	0,93	0,60	0,74	1,32
СКО, мг/м3	1,17	0,54	0,34	0,93	0,75	0,32	0,52	0,91

Осредненный суточный ход исследуемой величины

3 месяц

Часы (центральные диапазона)	0	3	6	9	12	15	18	21
Среднее значение, мг/м3	0,71	0,65	0,52	0,91	0,88	0,64	0,67	0,87
СКО, мг/м3	0,86	1,1	0,73	0,94	0,56	0,24	0,29	0,87

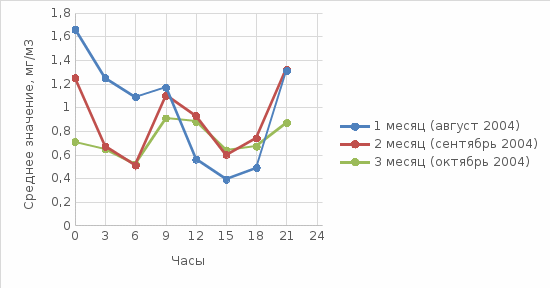Рис.3.1. Осредненный суточный ход



Рис.3.2. Зависимость среднего от СКО (показан линейный тренд)


На рис. 3.1. наносим значение ПДК и среднего по всему ряду.
Выводы:

• 
  суточный ход имеет такой вид из-за различных метеоусловий, а также загруженности транспортными средствами места проведения замеров
  
• 
  осредненный суточный ход превышал ПДК с августе 2004 года с 0 до 3 часов .
  
• 
  что значит: СКО много больше среднего или наоборот, много меньше? Если СКО меньше среднего, это значит, что величина большинства значений близка к среднему, если больше, то это говорит о большом разбросе значений.