Отчет по практике. Отчет по практике ИТб-2302-02-20. Отчет по учебной практике елькин Данил Романович

• Название: Отчет по учебной практике елькин Данил Романович
• Анкор: Отчет по практике
• Дата: 27.06.2022
• Размер: 119.26 Kb.
• Имя файла: Отчет по практике ИТб-2302-02-20.docx
• Тип: Отчет; #617817

ОТЧЕТ

ПО УЧЕБНОЙ ПРАКТИКЕ

Елькин Данил Романович
(Ф.И.О. обучающегося)
09.03.02 Информационные системы и технологии, 02 Информационные системы и технологии управления технологическими процессами в промышленности
(направление подготовки (специальность), направленность (профиль))
Место прохождения практики		ФГБОУ ВО «Вятский государственный университет»,
	(наименование организации, структурного подразделения организации)
кафедра САУ
(наименование организации, структурного подразделения организации)

Итоговая оценка:
Руководитель практики от университета					Ланских Ю.В.
	(дата)		(подпись)		(Ф.И.О.)

Киров, 2022 г.

Содержание

Введение 3

Основная часть 4

Введение в программирование на Python 4

Решение задачи кластеризации 5

Решение задачи классификации 6

Работа с математической статистикой 8

Реализация криптографического алгоритма 10

Заключение 12

Список источников 13

ПРИЛОЖЕНИЕ А 14

ПРИЛОЖЕНИЕ Б 15

ПРИЛОЖЕНИЕ В 16

ПРИЛОЖЕНИЕ Г 17

ПРИЛОЖЕНИЕ Д 18

Введение

В период с 20.06.2022 по 02.07.2022 года была пройдена учебная практика.

Целью данной практики стало выполнение обучающего задания, приведённое в методических указаниях (введение в программирование на Python, решение задачи кластеризации, решение задачи классификации, математическая статистика), для ознакомления с методами работы с языком Python.

На период учебной практики были поставлены следующие задачи:

1. 
   Пройти инструктаж по ознакомлению с правилами внутреннего трудового распорядка, охраны труда, техники безопасности, противопожарной безопасности, санитарно-эпидемиологическими правилами и гигиеническими нормативами, а также вводный инструктаж и инструктаж на рабочем месте 20.06.2022
   
2. 
   Выполнить обучающие задания, приведённые в методических указаниях (введение в программирование на Python, решение задачи кластеризации, решение задачи классификации, математическая статистика), для ознакомления с методами работы с языком Python. Провести анализ полученного фактического материала, представить его в текстовой и графической формах.
   
3. 
   Реализовать криптографический алгоритм (RSA-шифрование (цифровая подпись)) при помощи языка Python, не используя библиотечные функции, связанные непосредственно с шифрованием. Разработанная программа должна осуществлять шифрование и дешифрование текста в соответствии с вариантом. В приложении должна быть реализована возможность ввода текста (вручную или загрузка из файла – на усмотрение разработчика), ключа (если этого требует алгоритм) и зашифрованного текста.
   

5. Оформить отчёт по учебной практике.

Основная часть

Введение в программирование на Python

Задание

Выполнить задание из методических указаний №1.
Решение

1. 
   Изучить работу с интерпретатором Python.
   
2. 
   Изучить базовые возможности языка Python.
   

Блок схема алгоритма решения задачи представлена на рисунке 1:




Рисунок 1. Блок схема алгоритма решения задачи 1
Листинг кода представлен в ПРИЛОЖЕНИИ А.
Скриншот результата работы программы представлен на рисунке 2.

Рисунок 2. Скриншот результата работы программы задачи.

Решение задачи кластеризации

Задание

Выполнить задание из методических указаний №2.
Решение

1. 
   Задается количество кластеров k, которые требуется обнаружить
   
2. 
   Центры кластеров изначально инициализируются случайным образом
   
3. 
   Каждый из объектов приписывается к ближайшему кластеру
   
4. 
   На основании объектов, вошедших в каждый кластер, центры кластеров пересчитываются
   
5. 
   Шаги 3 и 4 повторяются до тех пор, пока центры кластеров не стабилизируются, то есть на очередной итерации объекты будут принадлежать тем же кластерам, что и до этого.
   

Блок схема алгоритма решения задачи представлена на рисунке 3:




Рисунок 3. Блок схема алгоритма решения задачи 3
Листинг кода представлен в ПРИЛОЖЕНИИ Б.
Скриншот результата работы программы представлен на рисунке 4.

Рисунок 4. Скриншот результата работы программы задачи.

Решение задачи классификации

Задание

Выполнить задание из методических указаний №3.
Решение

Пусть у нас имеется матрица объектов X. Каждая строка таблицы описывает отдельный объект. Каждый столбец таблицы описывает определенный признак объекта (рост, вес и т.п.). Кроме того, в матрице есть еще один столбец, описывающий класс, к которому принадлежит объект (см. рисунок ниже).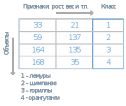



Пусть имеется объект obj, обладающий набором признаков, который необходимо отнести к заданному классу. Например, в нашем случае, obj будет представлять собой отдельную особь с признаками «рост» и «вес».

Чтобы определить, к какому классу принадлежит объект, нужно найти k ближайших к нему соседей (точек) и посмотреть, какой класс у этих соседей встречается чаще всего. Этому классу и будет принадлежать наш классифицируемый объект.

1. 
   Измеряем расстояние от объекта obj до каждого объекта в матрице X.
   
2. 
   Сортируем полученные значения в порядке увеличения расстояния (в начале будут объекты наиболее близкие к obj, в конце – наиболее удаленные).
   
3. 
   Берем первые k объектов из отсортированного списка, определяем, какой класс встречается там чаще всего. Именно этому классу и принадлежит наш объект obj.
   

Блок схема алгоритма решения задачи представлена на рисунке 5:




Рисунок 5. Блок схема алгоритма решения задачи 5
Листинг кода представлен в ПРИЛОЖЕНИИ В.
Скриншот результата работы программы представлен на рисунке 6.

Рисунок 6. Скриншот результата работы программы задачи.

Работа с математической статистикой

Задание

Выполнить задание из методических указаний №4.
Решение

1. 
   Создать в Python переменную, массив, матрицу с заданными, случайными целочисленными, нулевыми, единичными значениями
   
2. 
   Импортировать переменную (матрицу) из текстового структурированного файла (файл создать вручную: разделители столбцов – пробелы)
   
3. 
   Загрузить одномерные данные из каталога data/1D из файла с расширением .mat согласно варианта. Оценить параметры одномерной случайной величины, используя команды NumPy: np.max, np.min, np.median, np.mean, np.var, np.std; Команды сохранить в скрипт.
   
4. 
   Вывести графики одномерных случайных величин и их плотности распределения. Команды сохранить в скрипт. Подобрать вид распределения одномерной случайной величины и параметры. На одном графике отобразить случайную величину, уровень среднего значения и дисперсию.
   
5. 
   Построить и вывести на графике автокорреляцию заданной одномерной случайной величины. Команды сохранить в скрипт.
   
6. 
   Импортировать из каталога data/NDфайл *.matс многомерными данными согласно варианта. Первые 5 столбцов считать входными значениями (измерения датчиков, наблюдения и т.д.), последний 6 столбец – выходная величина, для которой требуется установить зависимость от входных величин.
   
7. 
   Построить матрицу корреляции для всех входных и выходных величин. Сделать выводы о зависимости/независимости выходной величины от каждой из входных компонент. Отобразить точечный график для случайных величин, коэффициент корреляции Пирсона для которых по модулю больше 0.8.
   

Блок схема алгоритма решения задачи представлена на рисунке 7:




Рисунок 5. Блок схема алгоритма решения задачи 7
Листинг кода представлен в ПРИЛОЖЕНИИ Г.
Скриншот результата работы программы представлен на рисунке 8.

Рисунок 8. Скриншот результата работы программы задачи.

Реализация криптографического алгоритма

Задание

Реализовать криптографический алгоритм (RSA-шифрование (цифровая подпись)) при помощи языка Python, не используя библиотечные функции, связанные непосредственно с шифрованием. Разработанная программа должна осуществлять шифрование и дешифрование текста в соответствии с вариантом. В приложении должна быть реализована возможность ввода текста (вручную или загрузка из файла – на усмотрение разработчика), ключа (если этого требует алгоритм) и зашифрованного текста.
Решение

В алгоритме RSA есть пять важных цифровых элементов:

P, q: это два неравных простых числа, случайно выбранных

N: n = p * q, которое является произведением p и q

Φ (n): φ (n) = (p-1) (q-1), который является произведением p-1 и q-1

E: случайным образом выберите положительное целое число, взаимно простое с φ (n). И убедитесь, что e <φ (n)

d: Согласно ed ≡ 1 (mod φ (n)), вычислить модульный обратный элемент d для φ (n)

ed ≡ 1 (mod φ (n)) означает, что после деления ed φ (n) остаток равен 1.

То есть ed = k * φ (n) +1
Можно рассматривать как

ed = φ (n) x + 1, наконец, используйте метод деления по очереди (посмотрел логику вывода в Интернете, я думаю, что это чисто математическая область, не имеет смысла вспоминать чисто), вы можете вычислить набор удовлетворительных решений (d, x) .

Таким образом, (n, e) - открытый ключ, а (n, d) - закрытый ключ.

1. 
   После создания цифровой последовательности. Зашифруйте по очереди в соответствии со следующим:
   

Открытый ключ (n, e), исходный m

m^e ≡ c (mod n)

Другими словами, c равно остатку от деления m ^ e на n.

То есть для вычисления зашифрованного текста c

2. 
   Отправьте зашифрованный текст в дешифратор, и дешифратор в свою очередь восстановит следующее:
   

c ^ d ≡ m (mod n) формула

Другими словами, m равно остатку от деления c ^ d на n.

Обратно найти m — это открытый текст
Блок схема алгоритма решения задачи представлена на рисунке 9:




Рисунок 5. Блок схема алгоритма решения задачи 9
Листинг кода представлен в ПРИЛОЖЕНИИ Д.
Скриншот результата работы программы представлен на рисунке 10.

Рисунок 10. Скриншот результата работы программы задачи.

Заключение

В соответствии с задачами, поставленными на период учебной практики, можно сделать следующие выводы о проделанной работе:

1. 
   Были выполнить обучающие задания, приведённые в методических указаниях для ознакомления с методами работы с языком Python:
   

• 
  Введение в программирование на Python;
  
• 
  Решение задачи кластеризации;
  
• 
  Решение задачи классификации;
  
• 
  Математическая статистика.
  

2. 
   Был проведен анализ полученного фактического материала.
   
3. 
   Было реализовано задание по реализации криптографического алгоритма (RSA-шифрование (цифровая подпись)) при помощи языка Python, не используя библиотечные функции, связанные непосредственно с шифрованием.
   
4. 
   Сформирован отчёт по учебной практике.
   

Список источников

ПРИЛОЖЕНИЕ А

(обязательное)

Программный код введения в программирование на Python

ПРИЛОЖЕНИЕ Б

(обязательное)

Программный код решения задачи кластеризации

ПРИЛОЖЕНИЕ В

(обязательное)

Программный код решения задачи классификации

ПРИЛОЖЕНИЕ Г

(обязательное)

Работа с математической статистикой

ПРИЛОЖЕНИЕ Д

(обязательное)

Реализация криптографического алгоритма