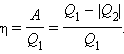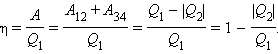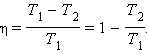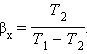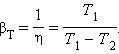Отчет, Тарасов, лекция2. Отчет по второй лекции студент группы баэ01о2101 очного отделения Тарасов Н. Э
 Скачать 0.79 Mb.
|
|
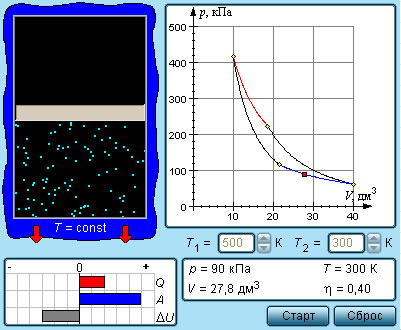
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Уфимский государственный нефтяной технический университет» Кафедра «Электротехника и электрооборудование предприятий» ОБЩАЯ ЭНЕРГЕТИКА Отчет по второй лекции Выполнил: студент группы № БАЭ01о–21–01 очного отделения Тарасов Н.Э. Проверил: профессор, доктор наук Андрианова Л.П. Уфа, 2022 г. Термодинамика – это раздел физики, изучающий тепловые свойства макроскопических тел и систем тел, находящихся в состоянии теплового равновесия, на основе закона сохранения энергии, без учета внутреннего строения тел, составляющих систему. Термодинамические параметры – физические величины, характеризующие состояние термодинамической системы (температура, объем, плотность, давление, масса, намагниченность, электрическая поляризация, теплоемкость при постоянном объеме и другие), т.е. любые признаки, имеющие количественную меру и относящиеся к системе в целом или к ее макроскопическим частям (кроме характеристик потоков энергии и массы, в размерность которых входит время). Свойства, заимствованные термодинамикой у физики, химии, техники приобретают в ней иное содержание, так как рассматриваются в зависимости от типичной термодинамической характеристики – температуры. Благодаря температуре различные свойства оказываются связанными между собой. Основными процессами в термодинамике являются: изохорный, протекающий при постоянном объеме; изобарный, протекающий при постоянном давлении; изотермический, происходящий при постоянной температуре; адиабатный, при котором теплообмен с окружающей средой отсутствует; При исследовании термодинамических процессов определяют: уравнение процесса в p—v иT—s координатах; связь между параметрами состояния газа; изменение внутренней энергии; величину внешней работы; количество подведенной теплоты на осуществление процесса или количество отведенной теплоты. Изохорный процесс 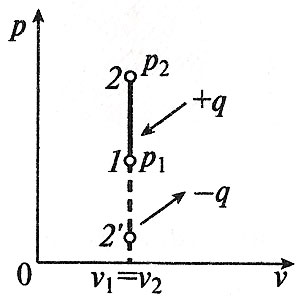 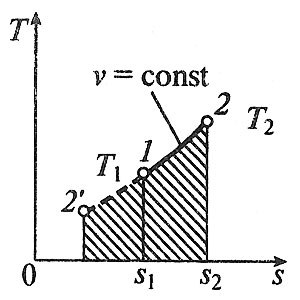 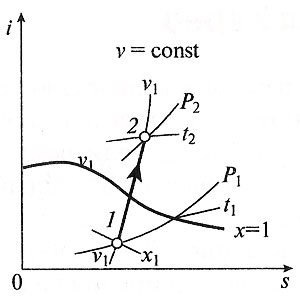 Изохорный процесс в p, v— , T, s— и i, s-координатах (диаграммах) При изохорном процессе выполняется условие v = const. Из уравнения состояния идеального газа (pv = RT) следует: p/T = R/v = const, т. е. давление газа прямо пропорционально его абсолютной температуре: p2/p1 = T2/T1. Работа расширения в изохорном процессе равна нулю (l = 0), так как объем рабочего тела не меняется (Δv = const). Количество теплоты, подведенной к рабочему телу в процессе 1-2 при cv = const определяется по формуле: q= cv(T2 — T1). Т. к.l = 0, то на основании первого закона термодинамики Δu = q, а значит изменение внутренней энергии можно определить по формуле: Δu = cv(T2 — T1). Изменение энтропии в изохорном процессе определяется по формуле: s2 – s1= Δs = cvln(p2/p1) = cvln(T2/T1). Изобарный процесс 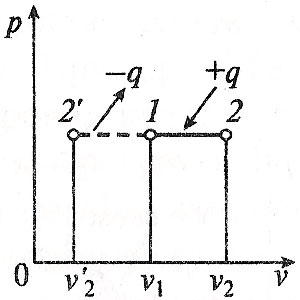 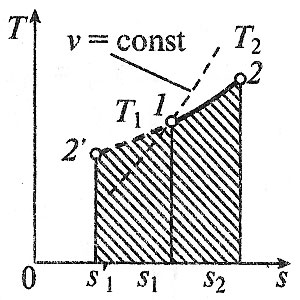 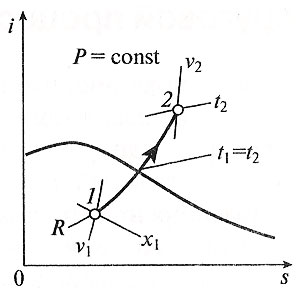 Изобарный процесс в p, v— , T, s— и i, s-координатах (диаграммах) Изобарным называется процесс, протекающий при постоянном давлении p = const. Из уравнения состояния идеального газа слуедует: v/T = R/p = const или v2/v1 = T2/T1, т. е. в изобарном процессе объем газа пропорционален его абсолютной температуре. Работа будет равна: l = p(v2 – v1). Т. к. pv1 = RT1 и pv2 = RT2, то l = R(T2 – T1). Количество теплоты при cp = const определяется по формуле: q = cp(T2 – T1). Изменение энтропии будет равно: s2 – s1= Δs = cpln(T2/T1). Изотермический процесс 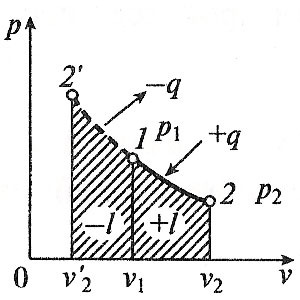 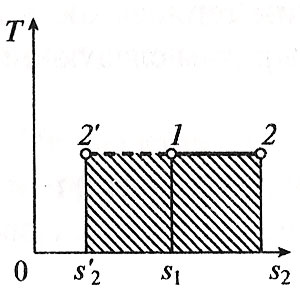 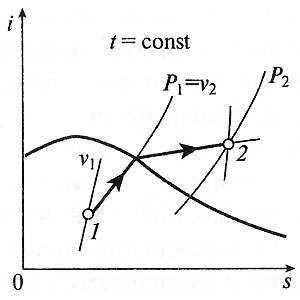 Изотермический процесс в p, v— , T, s— и i, s-координатах (диаграммах) При изотермическом процессе температура рабочего тела остается постоянной T = const, следовательно: pv = RT = const или p2/p1 = v1/v2, т. е. давление и объем обратно пропорциональны друг другу, так что при изотермическом сжатии давление газа возрастает, а при расширении – снижается. Работа процесса будет равна: l = RTln (v2 – v1) = RTln (p1 – p2). Так как температура остается неизменной, то и внутренняя энергия идеального газа в изотермическом процессе остается постоянной (Δu = 0) и вся подводимая к рабочему телу теплота полностью превращается в работу расширения: q = l. При изотермическом сжатии от рабочего тела отводится теплота в количестве, равном затраченной на сжатие работе. Изменение энтропии равно: s2 – s1= Δs = Rln(p1/p2) = Rln(v2/v1). Адиабатный процесс 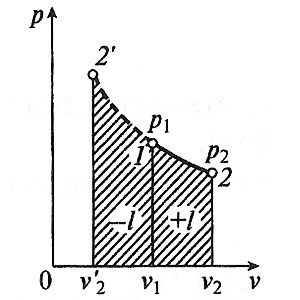 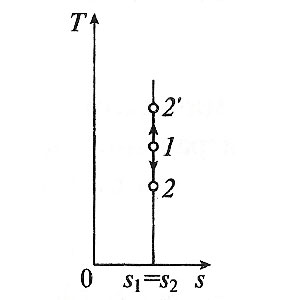 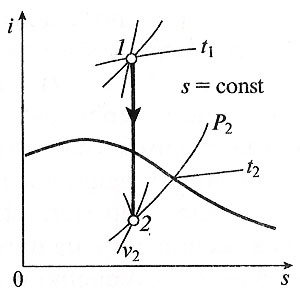 Адиабатный процесс в p, v— , T, s— и i, s-координатах (диаграммах) Адиабатным называется процесс изменения состояния газа, который происзодит без теплообмена с окружающей средой. Так как dq = 0, то уравнение первого закона термодинамики для адиабатного процесса будет иметь вид: du + pdv = 0 или Δu+ l = 0, следовательно Δu= —l. В адиабатном процессе работа расширения совершается только за счет расходования внутренней энергии газа, а при сжатии, происходящем за счет действия внешних сил, вся совершаемая ими работа идет на увеличение внутренней энергии газа. Обозначим теплоемкость в адиабатном процессе через cад, и условие dq = 0 выразим следующим образом: dq = cадdT = 0. Это условие говорит о том, что теплоемкость в адиабатном процессе равна нулю (cад = 0). Известно, что сp/cv = k и уравнение кривой адиабатного процесса (адиабаты) в p, v-диаграмме имеет вид: pvk = const. В этом выражении k носит название показателя адиабаты (так же ее называют коэффициентом Пуассона). Значения показателя адиабаты k для некоторых газов: kвоздуха = 1,4 kперегретого пара = 1,3 kвыхлопных газов ДВС = 1,33 kнасыщенного влажного пара = 1,135 Из предыдущих формул следует: l= — Δu = cv(T1 – T2); i1 – i2= cp(T1 – T2). Техническая работа адиабатного процесса (lтехн) равна разности энтальпий начала и конца процесса (i1 – i2). Адиабатный процесс, происходящий без внутреннего трения в рабочем теле, называется изоэнтропийным. В T, s-диаграмме он изображается вертикальной линией. Обычно реальные адиабатные процессы протекают при наличии внутреннего трения в рабочем теле, в результате чего всегда выделяется теплота, которая сообщается самому рабочему телу. В таком случае ds > 0, и процесс называется реальным адиабатным процессом. Внутренняя энергия – это физическая величина, равная сумме кинетической энергии теплового движения частиц тела и потенциальной энергии их взаимодействия друг с другом. Обозначение – U, в СИ единица измерения – Джоуль (Дж). В термодинамике внутренняя энергия зависит от температуры и объема тела. Внутренняя энергия тел зависит от их температуры, массы и агрегатного состояния. С ростом температуры внутренняя энергия увеличивается. Наибольшая внутренняя энергия у вещества в газообразном состоянии, наименьшая – в твердом. Внутренняя энергия идеального газа представляет собой только кинетическую энергию теплового движения его частиц; потенциальная энергия взаимодействия частиц равна нулю. Внутренняя энергия идеального газа прямо пропорциональна его температуре, а от объема не зависит (молекулы идеального газа не взаимодействуют друг с другом):  где i – коэффициент, равный числу степеней свободы молекулы, ν – количество вещества, R – универсальная газовая постоянная, T – абсолютная температура. Число степеней свободы равно числу возможных движений частицы. Для одноатомных газов коэффициент i = 3, для двухатомных газов i = 5. На практике часто важно уметь находить изменение внутренней энергии: 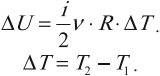 При решении задач можно записать формулу для вычисления внутренней энергии, используя уравнение Менделеева–Клапейрона:  где p – давление, V – объем газа. Внутренняя энергия реальных газов зависит как от температуры, так и от объема. Изменить внутреннюю энергию можно за счет изменения температуры (при теплопередаче) и за счет изменения давления и объема (при совершении работы). Если изменение внутренней энергии происходит только в результате совершения механической работы, то это изменение равно или работе внешних сил над системой  или работе системы против внешних сил   Работа в термодинамике — это одна из мер изменения внутренней энергии термодинамической системы. Работа газа Предположим, что в толстостенном цилиндре находится газ, сжимаемый поршнем. При сжатии поршень передает часть своей кинетической энергии молекулам газа, в результате чего увеличивается внутренняя энергия газа и повышается его температура — внешние силы совершают работу над газом. При расширении, наоборот, молекулы газа, передавая часть своей кинетической энергии поршню, уменьшают свою скорость и газ охлаждается - он совершает работу над внешними силами (b). 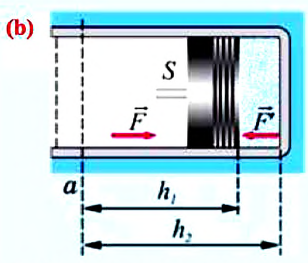 Таким образом, работа, совершенная газом над внешними силами, в результате расширении газа данной массы при постоянном давлении равна:  или  Работа же, совершенная внешними силами над газом равна :  Где  — сила, с которой газ действует на поршень,  — смещение поршня,  — давление газа,  — площадь поперечного сечения цилиндра,  — изменение объема газа. Совершенная работа численно равна площади фигуры, образованная графиком в системе координат  при расширении газа (т.е. при увеличении объема газа)  или  при сжатии же газа (т.е. при уменьшении объема газа)  или  (с).Если в процессе совершения работы газ через некоторое время возвращается в первоначальное состояние, то такой процесс называется замкнутым или циклическим процессом. Если стрелки, показывающие направление циклического процесса, совпадают с направлением вращения часовых стрелок, то работа газа положительна, а работа внешних сил отрицательна (d). Если же стрелки, определяющие направление процесса, направлены против вращения часовых стрелок, то работа газа отрицательна, а работа внешних сил положительна. 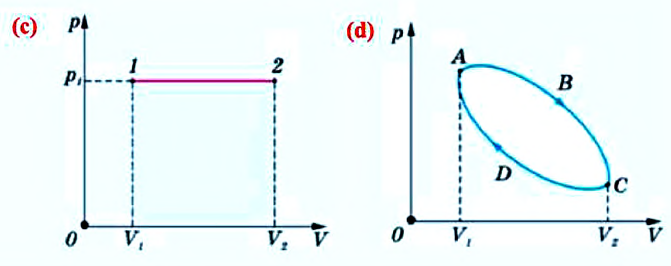 Q - энергия, которую тело теряет или приобретает при передаче тепла. Формула количества теплоты зависит от протекающего процесса. Формулы количества теплоты при некоторых процессах:  - Количество теплоты при нагревании и охлаждении. - Количество теплоты при плавлении или кристаллизации. - Количество теплоты при кипении, испарении жидкости и конденсации пара. - Количество теплоты при сгорании топлива.Закон сохранения и превращения энергии, распространенный на тепловые явления, называется первым законом (началом) термодинамики. Можно дать формулировку этого закона исходя из способов изменения внутренней энергии. Изменение внутренней энергии системы при переходе ее из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе:  Если рассматривать работу самой системы над внешними телами, то закон может быть сформулирован так: количество теплоты, переданное системе, идет на изменение ее внутренней энергии и совершение системой работы над внешними телами:  Если система изолирована и над ней не совершается работа и нет теплообмена с внешними телами, то в этом случае внутренняя энергия не изменяется. Если к системе не поступает теплота, то работа системой может совершаться только за счет уменьшения внутренней энергии. Это значит, что невозможно создать вечный двигатель – устройство, способное совершать работу без каких-либо затрат топлива. Первый закон термодинамики для изопроцессов Изотермический процесс: Q=A′(T=const,ΔU=0) Физический смысл: все переданное газу тепло идет на совершение работы. Изобарный процесс: Q=ΔU+A′ Физический смысл: подводимое к газу тепло идет на увеличение его внутренней энергии и на совершение газом работы. Изохорный процесс: Q=ΔU(V=const,A′=0) Физический смысл: внутренняя энергия газа увеличивается за счет подводимого тепла. Адиабатный процесс: ΔU=−A′ или A=ΔU(Q=0) Физический смысл: внутренняя энергия газа уменьшается за счет совершения газом работы. Температура газа при этом понижается. В ряде случаев оказывается целесообразным объединение параметров и и pv в общий калорический параметр, называемый энтальпией:  Энтальпия — термодинамическая функция, имеющая смысл полной (внутренней и внешней) энергии системы. Она складывается из внутренней энергии и и упругостной энергии pv, обусловленной наличием внешнего давления окружающей среды р, т.е. pv есть работа, которую надо затратить, чтобы ввести рабочее тело объемом v в среду, имеющую давление р. Для идеального газа справедливы соотношения:  При р = const можно получить:  Продифференцировав i - и + pv и подставив в дифференциальное уравнение первого закона термодинамики для потока рабочего тела, можно получить 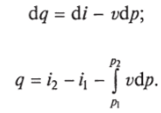 Энтальпия измеряется в тех же единицах, что и теплота, работа и внутренняя энергия (Дж/кг). Поскольку энтальпия, так же как и внутренняя энергия, является функцией состояния, то ее абсолютная величина может быть определена только с точностью до некоторой постоянной, условно выбранной для начала отсчета. По международному соглашению за начало отсчета энтальпии для воды и водяного пара принята так называемая тройная точка (Т = 273,16 К и р = 0,0006 Па), в которой возможно одновременное существование трех фаз: льда, жидкости и пара. За начало отсчета энтальпии для газов может быть принята температура Т- 0 К. Второй закон термодинамики. Второй закон термодинамики, как и первый, является опытным законом, основывающимся на многовековых наблюдениях ученых, однако установлен он был только в середине XIX в. Наблюдения за явлениями природы показывают, что возникновение и развитие самопроизвольно протекающих в ней естественных процессов, работа которых может быть использована для нужд человека, возможно лишь при отсутствии равновесия между участвующей в процессе термодинамической системой и окружающей средой. Эти процессы всегда характеризуются односторонним их протеканием от более высокого потенциала к более низкому (от более высокой температуры к более низкой или от более высокого давления к более низкому). При протекании указанных процессов термодинамическая система стремится к тому, чтобы прийти в равновесие с окружающей средой, характеризуемое равенством давления и температуры системы и окружающей среды. Из наблюдений за явлениями природы также следует, что для того чтобы заставить процесс протекать в направлении, обратном направлению протекания самопроизвольного процесса, необходимо затратить заимствованную из внешней среды энергию. В термодинамике пользуются еще одним параметром состояния рабочего тела — энтропией, устанавливающей связь между количеством теплоты и температурой (Р. Клаузиус, 1850). Поясним этот параметр на основе следующих соображений. Уравнение первого закона термодинамики можно записать в виде  В этом уравнении dq не является полным дифференциалом, поскольку в правую часть уравнения входит член d/, не являющийся полным дифференциалом, так как работа является не параметром состояния газа, а функцией процесса. Вследствие этого уравнение нельзя проинтегрировать в интервале двух произвольно выбранных состояний газа. Из математики известно, что всякий двучлен можно представить в виде полного дифференциала, если его умножить на так называемый интегрирующий множитель. При умножении на интегрирующий множитель 1 /Т (где Т — абсолютная температура), приведенное уравнение примет вид  Уравнение (1.6) можно представить в несколько ином виде, а именно:  Выражение (1.7) говорит о том, что dq/T представляет собой полный дифференциал некоторой функции s (т. е. dq/T = ds), являющейся параметром состояния газа, поскольку она зависит только от двух параметров состояния газа и поэтому не зависит от того, каким путем газ из одного состояния перешел в другое. Этот параметр состояния газа в общем случае называют энтропией газа и обозначают буквой S (Дж/К). Энтропию, отнесенную к 1 кг газа, называют удельной энтропией газа и обозначают буквой s [Дж/(кг- К)). Приведенное ранее уравнение dq = di - vdp также является неполным дифференциальным уравнением, поскольку dq не является полным дифференциалом. Однако и это уравнение при умножении его на интегрирующий множитель 1/7’ может быть приведено к виду полного дифференциального уравнения 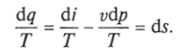 Следовательно, 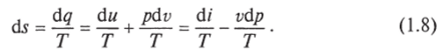 Учитывая, что для идеального газа pv = RT и, следовательно, 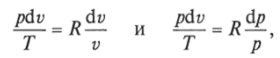 а также  уравнение (1.8) для идеального газа может быть преобразовано следующим образом: 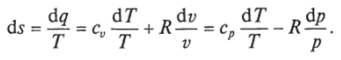 После интегрирования оно примет вид  Изменение энтропии в интервале между двумя состояниями газа (7 и 2) выражается уравнением 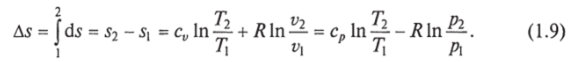 Из уравнения (1.9) следует, что количество теплоты, участвовавшее в том или ином термодинамическом процессе при изменении рабочего тела от состояния 7 до состояния 2, можно выразить следующим образом:  Этот интеграл можно вычислить, если известна функциональная зависимость между Tns. Пользуясь этой зависимостью, строят кривые в системе координат s— Т, отображающие те или иные термодинамические процессы. На основании выражения (1.10) можно заключить, что для процесса 1—2 площадь 7— 2—s2—sb лежащая под кривой, отображающей этот процесс, выражает количество теплоты, участвующее в этом процессе. 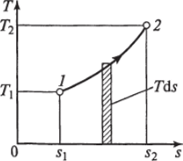 Графическое изображение подвода теплоты в 7’,.s-диаграмме Для определения численных значений энтропии пользуются началом отсчета при Т = 0 К, для которого i0 = 0. Физический смысл энтропии. Энтропию нельзя измерить, ее смысл затруднительно продемонстрировать с помощью наглядных пособий, но можно понять по следующим интерпретациям. Тепловым двигателем называется устройство, способное превращать полученное количество теплоты в механическую работу. Механическая работа в тепловых двигателях производится в процессе расширения некоторого вещества, которое называется рабочим телом. В качестве рабочего тела обычно используются газообразные вещества (пары бензина, воздух, водяной пар). Рабочее тело получает (или отдает) тепловую энергию в процессе теплообмена с телами, имеющими большой запас внутренней энергии. Эти тела называются тепловыми резервуарами. Как следует из первого закона термодинамики, полученное газом количество теплоты Q полностью превращается в работу A при изотермическом процессе, при котором внутренняя энергия остается неизменной (ΔU = 0):
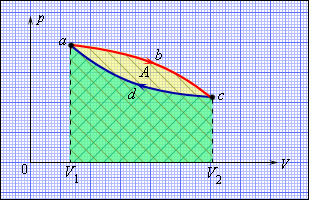
Но такой однократный акт преобразования теплоты в работу не представляет интереса для техники. Реально существующие тепловые двигатели (паровые машины, двигатели внутреннего сгорания и т. д.) работают циклически. Процесс теплопередачи и преобразования полученного количества теплоты в работу периодически повторяется. Для этого рабочее тело должно совершать круговой процесс или термодинамический цикл, при котором периодически восстанавливается исходное состояние. Круговые процессы изображаются на диаграмме (p, V) газообразного рабочего тела с помощью замкнутых кривых. При расширении газ совершает положительную работу A1, равную площади под кривой abc, при сжатии газ совершает отрицательную работу A2, равную по модулю площади под кривой cda. Полная работа за цикл A = A1 + A2 на диаграмме (p, V) равна площади цикла. Работа A положительна, если цикл обходится по часовой стрелке, и A отрицательна, если цикл обходится в противоположном направлении.
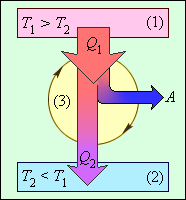
Общее свойство всех круговых процессов состоит в том, что их невозможно провести, приводя рабочее тело в тепловой контакт только с одним тепловым резервуаром. Их нужно, по крайней мере, два. Тепловой резервуар с более высокой температурой называют нагревателем, а с более низкой – холодильником. Совершая круговой процесс, рабочее тело получает от нагревателя некоторое количество теплоты Q1 > 0 и отдает холодильнику количество теплоты Q2 < 0. Полное количество теплоты Q, полученное рабочим телом за цикл, равно
При обходе цикла рабочее тело возвращается в первоначальное состояние, следовательно, изменение его внутренней энергии равно нулю (ΔU = 0). Согласно первому закону термодинамики,
Отсюда следует:
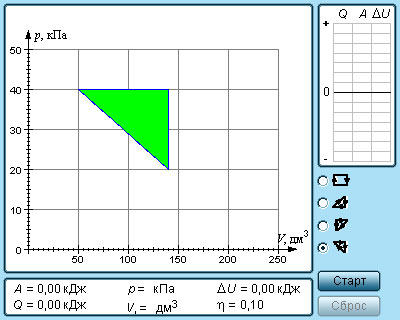
Работа A, совершаемая рабочим телом за цикл, равна полученному за цикл количеству теплоты Q. Отношение работы A к количеству теплоты Q1, полученному рабочим телом за цикл от нагревателя, называется коэффициентом полезного действия η тепловой машины:
Коэффициент полезного действия указывает, какая часть тепловой энергии, полученной рабочим телом от «горячего» теплового резервуара, превратилась в полезную работу. Остальная часть (1 – η) была «бесполезно» передана холодильнику. Коэффициент полезного действия тепловой машины всегда меньше единицы (η < 1).
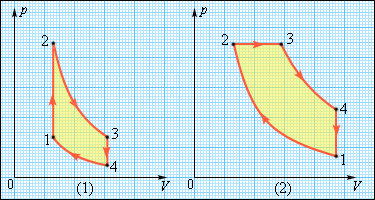
В двигателях, применяемых в технике, используются различные круговые процессы. В обоих случаях рабочим телом является смесь паров бензина или дизельного топлива с воздухом. Цикл карбюраторного двигателя внутреннего сгорания состоит из двух изохор (1–2, 3–4) и двух адиабат (2–3, 4–1). Дизельный двигатель внутреннего сгорания работает по циклу, состоящему из двух адиабат (1–2, 3–4), одной изобары (2–3) и одной изохоры (4–1). Реальный коэффициент полезного действия у карбюраторного двигателя порядка 30 %, у дизельного двигателя – порядка 40 %.
В 1824 году французский инженер С. Карно рассмотрел круговой процесс, состоящий из двух изотерм и двух адиабат, который сыграл важную роль в развитии учения о тепловых процессах. Он называется циклом Карно.
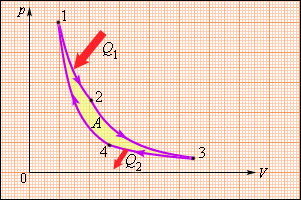
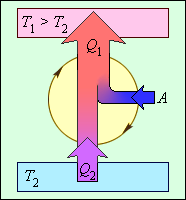
Цикл Карно совершает газ, находящийся в цилиндре под поршнем. На изотермическом участке (1–2) газ приводится в тепловой контакт с горячим тепловым резервуаром (нагревателем), имеющим температуру T1. Газ изотермически расширяется, совершая работу A12, при этом к газу подводится некоторое количество теплоты Q1 = A12. Далее на адиабатическом участке (2–3) газ помещается в адиабатическую оболочку и продолжает расширяться в отсутствие теплообмена. На этом участке газ совершает работу A23 > 0. Температура газа при адиабатическом расширении падает до значения T2. На следующем изотермическом участке (3–4) газ приводится в тепловой контакт с холодным тепловым резервуаром (холодильником) при температуре T2 < T1. Происходит процесс изотермического сжатия. Газ совершает работу A34 < 0 и отдает тепло Q2 < 0, равное произведенной работе A34. Внутренняя энергия газа не изменяется. Наконец, на последнем участке адиабатического сжатия газ вновь помещается в адиабатическую оболочку. При сжатии температура газа повышается до значения T1, газ совершает работу A41 < 0. Полная работа A, совершаемая газом за цикл, равна сумме работ на отдельных участках:
На диаграмме (p, V) эта работа равна площади цикла. Процессы на всех участках цикла Карно предполагаются квазистатическими. В частности, оба изотермических участка (1–2 и 3–4) проводятся при бесконечно малой разности температур между рабочим телом (газом) и тепловым резервуаром (нагревателем или холодильником). Как следует из первого закона термодинамики, работа газа при адиабатическом расширении (или сжатии) равна убыли ΔU его внутренней энергии. Для 1 моля газа
где T1 и T2 – начальная и конечная температуры газа. Отсюда следует, что работы, совершенные газом на двух адиабатических участках цикла Карно, одинаковы по модулю и противоположны по знакам
По определению, коэффициент полезного действия η цикла Карно есть
С. Карно выразил коэффициент полезного действия цикла через температуры нагревателя T1 и холодильника T2:
Цикл Карно замечателен тем, что на всех его участках отсутствует соприкосновение тел с различными температурами. Любое состояние рабочего тела (газа) на цикле является квазиравновесным, т. е. бесконечно близким к состоянию теплового равновесия с окружающими телами (тепловыми резервуарами или термостатами). Цикл Карно исключает теплообмен при конечной разности температур рабочего тела и окружающей среды (термостатов), когда тепло может передаваться без совершения работы. Поэтому цикл Карно – наиболее эффективный круговой процесс из всех возможных при заданных температурах нагревателя и холодильника:
Любой участок цикла Карно и весь цикл в целом может быть пройден в обоих направлениях. Обход цикла по часовой стрелке соответствует тепловому двигателю, когда полученное рабочим телом тепло частично превращается в полезную работу. Обход против часовой стрелки соответствует холодильной машине, когда некоторое количество теплоты отбирается от холодного резервуара и передается горячему резервуару за счет совершения внешней работы. Поэтому идеальное устройство, работающее по циклу Карно, называют обратимой тепловой машиной. В реальных холодильных машинах используются различные циклические процессы. Все холодильные циклы на диаграмме (p, V) обходятся против часовой стрелки.
Устройство, работающее по холодильному циклу, может иметь двоякое предназначение. Если полезным эффектом является отбор некоторого количества тепла |Q2| от охлаждаемых тел (например, от продуктов в камере холодильника), то такое устройство является обычным холодильником. Эффективность работы холодильника можно охарактеризовать отношением
т. е. эфективность работы холодильника – это количество тепла, отбираемого от охлаждаемых тел на 1 джоуль затраченной работы. При таком определении βх может быть и больше, и меньше единицы. Для обращенного цикла Карно
Если полезным эффектом является передача некоторого количества тепла |Q1| нагреваемым телам (например, воздуху в помещении), то такое устройство называется тепловым насосом. Эффективность βТ теплового насоса может быть определена как отношение
т. е. количеством теплоты, передаваемым более теплым телам на 1 джоуль затраченной работы. Из первого закона термодинамики следует:
следовательно, βТ всегда больше единицы. Для обращенного цикла Карно
Второй Закон термодинамики был сформулирован в работах физика Р.Клаузиуса. Он дал ему следующее определение: Невозможно перенести тепло от более холодной системы к более горячей без других изменений в обеих системах или окружающих телах. Замечание «без других изменений» принципиально. Оно говорит о том, что передача тепла от более холодного тела к горячему все же возможна, но при этом необходимо затратить дополнительную энергию. Второй Закон термодинамики распространяется на любые процессы, в которых изменяется внутренняя энергия тел. Превращение механической энергии в тепло также подчиняется этому закону. Обратный процесс, когда внутренняя энергия тела превратится в механическую, возможен только с затратами дополнительной энергии. Закон Дюлонга-Пти (Закон постоянства теплоёмкости) — эмпирический закон, согласно которому молярная теплоёмкость твёрдых тел при комнатной температуре близка к 3R:  где R — универсальная газовая постоянная. Закон выводится в предположении, что кристаллическая решетка тела состоит из атомов, каждый из которых совершает гармонические колебания в трех направлениях, определяемыми структурой решетки, причем колебания по различным направлениям абсолютно независимы друг от друга. При этом получается, что каждый атом представляет три осциллятора с энергией E, определяемой следующей формулой:  .Формула вытекает из теоремы о равнораспределении энергии по степеням свободы. Так как каждый осциллятор имеет одну степень свободы, то его средняя кинетическая энергия равна 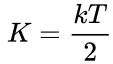 , а так как колебания происходят гармонически, то средняя потенциальная энергия равна средней кинетической, а полная энергия - соответственно их сумме. Число осцилляторов в одном моле вещества составляет  , их суммарная энергия численно равна теплоемкости тела - отсюда и вытекает закон Дюлонга-Пти. |
