кристалография. кристаллография. Структура. Кристаллическая (пространственная) решетка. Элементарная ячейка, ее параметры. Построение пространственной решетки
 Скачать 286.02 Kb. Скачать 286.02 Kb.
|
|
Структура. Кристаллическая (пространственная) решетка. Элементарная ячейка, ее параметры. Построение пространственной решетки. Кристаллическая структура — такая совокупность атомов, в которой с каждой точкой кристаллической решётки связана определённая группа атомов, называемая мотивной единицей, причем все такие группы одинаковые по составу, строению и ориентации относительно решётки. Кристаллическая решётка — вспомогательный геометрический образ, вводимый для анализа строения кристалла. Решётка имеет сходство с канвой или сеткой, что даёт основание называть точки решётки узлами. Решёткой является совокупность точек, которые возникают из отдельной произвольно выбранной точки кристалла под действием группы трансляции. Это расположение замечательно тем, что относительно каждой точки все остальные расположены совершенно одинаково. Применение к решётке в целом любой из присущих ей трансляций приводит к её параллельному переносу и совмещению. Для удобства анализа обычно точки решётки совмещают с центрами каких-либо атомов из числа входящих в кристалл, либо с элементами симметрии. В зависимости от пространственной симметрии, все кристаллические решётки подразделяются на семь кристаллических систем. По форме элементарной ячейки они могут быть разбиты на шесть сингоний. Все возможные сочетания имеющихся в кристаллической решётке поворотных осей симметрии и зеркальных плоскостей симметрии приводят к делению кристаллов на 32 класса симметрии, а с учётом винтовых осей симметрии и скользящих плоскостей симметрии на 230 пространственных групп. Пространственная решётка - простейшая геометрическая схема кристаллической решётки. Узел пространственной решётки символизирует частицы (атомы, ионы, молекулы) или их группы, симметрично повторяющиеся в структуре. Плоские сетки соответствуют граням кристалла, ряды - его ребрам. Всего можно образовать 14 типов пространственной решётки. Элементарная ячейка — минимальная ячейка, отвечающая единичной решёточной точке структуры с трансляционной симметрией в 2D, 3D или других размерностях. Фактически это минимальный воображаемый объём кристалла, параллельные переносы (трансляции) которого в трёх измерениях позволяют построить трёхмерную кристаллическую решётку в целом. Содержимое элементарной ячейки позволяет охарактеризовать всю структуру минерала. Часть структуры, охватываемая элементарной ячейкой, состоит из атомов, удерживаемых вместе благодаря электронным связям. Такие мельчайшие ячейки, бесконечно повторяющиеся в трехмерном пространстве, образуют кристалл. Применяемые в кристаллографии элементарные ячейки имеют вид параллелепипедов, их форма и размер определяются заданием трёх некомпланарных трансляций (векторов) решётки, то есть трёх не лежащих в одной плоскости ребер ячейки. Ячейка полностью определяет решётку. Ячейка, построенная на трёх кратчайших некомпланарных трансляциях решётки, называется основной ячейкой. Объём такой ячейки минимален, она содержит всего один узел кристаллической решётки, и относится поэтому к примитивным ячейкам. Элементы симметрии. Единичные и эквивалентно-равные направлениях в кристаллах. Элементы симметрии - это вспомогательные геометрические образы (плоскости, прямые линии, точки), с помощью которых обнаруживается симметрия фигур. Основные элементы симметрии: Плоскость симметрии - это воображаемая плоскость, которая делит фигуру на две равные части так, что одна из частей является зеркальным отражением другой. Плоскость симметрии обозначается буквой Р Ось симметрии - воображаемая прямая линия, при повороте вокруг которой всегда на один и тот же угол происходит совмещение равных частей фигуры. Наименьший угол поворота вокруг оси, приводящий к такому совмещению, называется элементарным углом поворота оси симметрии a. Его величина определяет порядок оси симметрии n, который равен числу самосовмещений при полном повороте фигуры на 360° (n = 360/a). Центр симметрии (центр инверсии) - это такая точка внутри фигуры при проведении через которую любая прямая встретит на равном от нее расстоянии одинаковые и обратно расположенные части фигуры. Центр симметрии обозначается буквой С. Если каждая грань кристалла имеет себе равную и параллельную или обратно параллельную, то данный кристалл обладает центром симметрии. Некоторые кристаллы могут не иметь центра симметрии. Кристаллы высшей категории не имеют единичных направлений, у них обязательно есть несколько осей порядка выше чем 2, в частности четыре оси 3, расположенные как пространственные диагонали куба. Это высокосимметричные кристаллы. Любому направлению в кристалле высшей категории соответствуют другие симметрично эквивалентные направления. Свойства кристаллов в направлениях симметрично эквивалентных должны быть одинаковыми, поэтому анизотропия свойств в кристаллах высшей категории выражена слабее всего. Многие физические свойства (электропроводность, теплопроводность, показатель преломления) в этих кристаллах изотропны как в аморфных веществах, а анизотропия других свойств (упругость, электрооптический эффект) гораздо слабее, чем у кристаллов других категорий. Внешняя форма кристаллов высшей категории, как правило, изометрична, т. е. развита примерно одинаково во все стороны, как куб, октаэдр, тетраэдр. Кристаллы средней категории имеют одно особое направление, а именно: одна ось симметрии 3, 4 или 6, простая или инверсионная. Анизотропия физических свойств у этих кристаллов гораздо сильнее, чем у кристаллов высшей категории. Особенно заметно различие свойств вдоль и поперек главной оси симметрии. Характерные формы кристаллов средней категории — призмы, пирамиды и др. К низшей категории относятся кристаллы, у которых нет осей симметрии порядка выше чем 2, а единичных направлений несколько. Это наименее симметричные кристаллы с ярко выраженной анизотропией свойств. Классификация кристаллов по категориям и системам (сингониям). Их характеристики. Разбиение кристаллов по категориям основано на возможности выделения единичных направлений. Единичным направлением называется такое направление, которое преобразуется само в себя при действии всех элементов симметрии данного класса. Чем меньше единичных направлений в кристалле, тем более он симметричен. Возможны следующие случаи В кристаллах, в которых возможно выделение нескольких единичных направлений, относят к низшей категории. Такие кристаллы обладают наиболее ярко выраженной анизотропией свойств. В кристаллах, в которых существует единственное единичное направление, относят к средней категории. В таких кристаллах свойства вдоль единичного направления обычно сильно отличаются от свойств во всех других направлениях. И, наконец, кристаллы, в которых нет единичных направлений, относят к высшей категории. Свойства таких кристаллов близки к изотропным. Распределение кристаллов по кристаллическим системам основано на выделении общих, одинаковых по типу и расположению, элементов симметрии. Эти элементы симметрии называют определяющими элементами симметрии. Всего возможно семь кристаллических систем 1. В кристаллах триклинной системы может не быть ни одного элемента симметрии (ось первого порядка) или быть только центр симметрии (инверсионная ось первого порядка). 2. В кристаллах моноклинной системы может быть только одна ось второго порядка, возможно, инверсионная (плоскость симметрии). 3. В ромбических кристаллах должны быть три оси второго порядка, возможно, инверсионных. 4. В тригональных кристаллах должна быть одна ось третьего порядка, возможно, инверсионная. 5. В тетрагональных кристаллах должна быть одна ось четвертого порядка, возможно, инверсионная. 6. В гексагональных кристаллах должна быть одна ось шестого порядка, возможно, инверсионная. 7. В кубических кристаллах должно быть четыре оси третьего порядка. В соответствии с приведенным выше анализом возможных элементов симметрии в кристаллах различных категорий, можно сделать вывод о том, что: к низшей категории принадлежат кристаллы триклинной, моноклинной и ромбической системы; к средней – кристаллы тригональной, тетрагональной и гексагональной системы; к высшей – кристаллы кубической системы. Формы кристаллических многогранников. Простые и комбинированные формы. Простая форма- это совокупность граней кристалла одинакового размера и формы, связанная элементами симметрии Комбинированная форма- совокупность простых форм. Формы: открытые, закрытые Открытые: не образуют замкнутого пространства со всех сторон (призмы, пирамиды) Замкнутые, образуют замкнутое пространство (куб, октаэдр) 32 класса симметрии. Вывод и описание. Теоремы о сложении элементов симметрии. 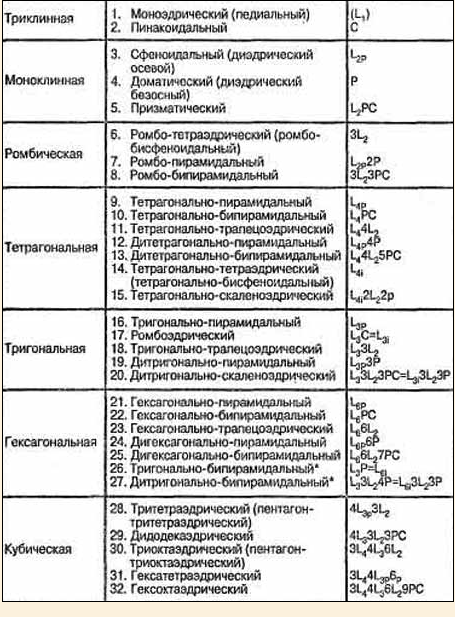 Симметрия структуры кристаллов. Решетки Бравэ. Распределение элементарных ячеек по сингониям. Координационные числа структурных единиц. Координационные многогранники. Число атомов в ячейке. Определение стехиометрических формулы вещества. Размеры атомов и ионов. Эффективные и действительные размеры. Зависимость их от положения элемента в периодической системе для s-, p-, f- элементов, от координационного числа заряда. Поляризация ионов. Кристаллическая структура. Ионные, металлические кристаллы. Особенности координирования в них СЕ. Примеры. Молекулярный кристалл — кристалл, образованный из молекул. Молекулы связаны между собой слабыми ван-дер-ваальсовыми силами, внутри же молекул между атомами действует более прочная ковалентная связь. Большинство молекулярных кристаллов — кристаллы органических соединений, типичный такой кристалл — нафталин. Молекулярные кристаллы образуют также некоторые простые вещества (водород, галогены, азот, кислород), бинарные соединения типа H2O, CO2, N2O4, металлоорганические соединения и некоторые комплексные соединения. К молекулярным кристаллам относятся и кристаллы полимеров, а также кристаллы белков, нуклеиновых кислот. Особым случаем молекулярных кристаллов являются кристаллы отвердевших инертных газов, в которых ван-дер-ваальсовы силы связывают между собой не молекулы, а атомы. Для типичных молекулярных кристаллов характерны низкие температуры плавления, большие коэффициенты теплового расширения, высокая сжимаемость, малая твёрдость. В обычных условиях большинство молекулярных кристаллов — диэлектрики. Некоторые молекулярные кристаллы, например, органические красители, — полупроводники. Класс соединений с нормальной валентностью характеризуется жесткими направленными связями, аналогичными по своей природе связям в решетке алмаза. При этом каждый атом оказывается окруженным четырьмя другими, с которыми он связан нормальными ковалентными связями из двух электронов, следовательно, в данном случае электронная концентрация равна 4. Например, в соединении AlSb каждый атом алюминия имеет три электрона, а каждый атом сурьмы — пять. Следовательно, на два атома приходится восемь электронов и, таким образом, электронная концентрация равна четырем. Эти соединения кристаллизуются в решетку цинковой обманки, которая совершенно аналогична решетке алмаза, с той лишь разницей, что атомы углерода заменены атомами двух сортов: цинка и серы. Металлический кристалл рассматривается как состоящий из правильно расположенных положительных ионов, удерживаемых совместно путем притяжения находящихся между ними электронов. Структуры металлических кристаллов характеризуются плотной и плотнейшей упаковкой положительных ионов. металлы демонстрируют высокую тепло - и электропроводность, указывая на присутствие электронов, которые являются относительно свободными для движения через кристалл. Металлические кристаллы образуются следующим образом. При кристаллизации атомы сближаются, валентные электроны отделяются от атомов и коллективизируются — они уже принадлежат не отдельным атомам, а кристаллической решетке в целом. Совокупность этих свободных электронов образует электронный газ. Кристаллическая решетка состоит из плотно упакованных положительно заряженных ионов, которые удерживаются в узлах решетки за счет взаимодействия с отрицательно заряженным электронным газом. Наличие свободных электронов и служит причиной того, что металлы — хорошие проводники электричества. Ионные кристаллы образуются путем плотной упаковки ионов, заряженных разноименно. К числу ионных кристаллов относится большинство неорганических соединений, например, соли. Рассмотрим строение кристалла поваренной соли — хлорида натрия NаСI. Известно, что атом натрия легко отдает свой валентный электрон, а атом хлора его принимает. Образуются два иона: положительный Nа+ и отрицательный Сl-. У обоих ионов внешняя электронная оболочка оказывается заполненной, ибо она содержит по 8 электронов. Электроны располагаются сферически, симметрично относительно ядер, так что оба иона можно считать шариками, но с разными радиусами: ион хлора больше иона натрия. Между разноименно заряженными ионами действуют кулоновские силы притяжения, удерживающие их в узлах кубической кристаллической решетки. Каждый ион натрия окружен шестью ионами хлора, и, наоборот, каждый ион хлора окружен шестью ионами натрия. В кристалле нет молекул NаСl. Ионные кристаллы. Координационные принципы строения ионных кристаллов. Зависимость между видом координационного полиэдра (координационным числом) и отношением радиуса катиона к радиусу аниона. Правила Магнуса-Гольдшмидта. Ионные кристаллы. Координационные принципы строения ионных кристаллов. Зависимость между видом координационного полиэдра (координационным числом) и отношением радиуса катиона (rk) к радиусу аниона (ra). Правило Магнуса-Гольдшмидта.
Ионные кристаллы образуются ионной связью. Ионная связь — это электростатическая связь между катионами и анионами. Ионная связь малонаправленная и ненасыщаемая. Основные свойства: характерны диэлектрические свойства, вещества хрупкие, обладают низкой электро- и теплопроводимостью. Энергия связи ионных структур в пределах 120-180 ккалл/моль. Ионы с заполненными валентными оболочками обладают сферической симметрией. Кулоновские силы между ионами (ионная связь) с большой степенью приближения можно считать центральными силами. Однако отличие случая ионной связи от задачи о плотных шаровых упаковках заключается в том, что ионы имеют различные ионные радиусы (− радиус катиона, − радиус аниона) и электрические заряды разного знака. Образование катионов и анионов из нейтральных атомов происходит соответственно путем отдачи и присоединения внешних электронов. Поэтому, как правило, радиусы анионов больше радиусов катионов. Понятие о радиусе иона является, конечно, не чисто геометрическим и характеризует радиус «сферы действия» данного иона. Анионы − основные по объему «кирпичи» в структуре ионного кристалла Правила Магнуса - Гольдшмидта - КЧ катиона определяется тем отношением его радиуса к радиусу аниона, при котором наступает соприкосновение между собой и «расталкивание» соседних анионов. Плотнейшие упаковки. Степени заполнения пространства структурными единицами. Типы пустот в решетках. Плотнейшие упаковки, в кристаллографии, формы расположения атомов в кристаллической решетке, которые характеризуются наибольшим числом атомов в единице объема кристалла. Для устойчивости кристаллической структуры требуется условие минимума ее потенциальной энергии. Реализацию этого условия обеспечивает плотнейшая упаковка структурных единиц при их максимальном сближении. Плотноупакованными называются решетки, в которых при заданном минимальном расстоянии между узлами достигается максимальная концентрация узлов в единице объема. Тенденция к осуществлению плотнейшей упаковки сильнее всего выражена в металлических и ионных структурах, а также характерна для кристаллизованных инертных газов. В этих случаях связи не направлены, и атомы или ионы можно считать сферическими. В плоском слое шаров, плотнейшим образом прилегающих друг к другу, каждый шар соприкасается с шестью шарами и окружен шестью лунками (пустотами), а каждая из лунок — тремя шарами. Такое расположение атомов характерно для плоскостей {111} гранецентрированной кубической структуры и плоскости базиса (0001) гексагональной плотноупакованной структуры. Координационное число 12 — обязательный признак плотнейшей упаковки. Для шаров кубической упаковки координационный полиэдр (многогранник) – кубооктаэдр, а для гексагональной — гексагональный кубооктаэдр. Двухслойная гексагональная плотная упаковка или ГПУ, соответствующая чередованию слоев ABAB... очень распространена. Она характерна для Be, Mg, Zn, Ti. Третий распространенный тип кристаллической структуры называется объемно-центрированный кубический или ОЦК. Атомы в такой структуре занимают вершины и центр куба. ОЦК-структура немного менее плотно упакована, чем ГЦК или ГПУ и часто это высокотемпературная форма металлов, которые более плотно упакованы при низких температурах. К примеру, структура железа (Fe) может быть либо ГЦК либо ОЦК в зависимости от температуры, тогда как металлы, такие как хром, всегда имеют ОЦК-структуру. Коэффициент компактности для ОЦК равен К =0,68. Все пустоты ОЦК - тетраэдрические. Плотные упаковки характерны для структур с ненаправленными связями. Существуют упаковки четырехслойные, пятислойные и т. п. Четырехслойная упаковка характерна для редкоземельных металлов La, Ce и др. Известны структуры с многослойной упаковкой, состоящей из десятков и сотен слоев (политипия). Весьма часто полиморфизм (уже не только чистых металлов, но и соединений с простейшей формулой АХ) сводится к смене многослойных плотнейших упаковок (6-, 8-, 15-слойных) вплоть до числа слоев в несколько десятков, как например, в карбиде кремния SiC. Формирование типа упаковки определяется силами дальнодействия между атомами. Структуры многих неорганических (ионных) кристаллов представляют собой плотнейшие упаковки шаровых анионов (с большими ионными радиусами), в пустотах которых распределяются мелкие катионы. Пространственные решетки Бравэ, их обозначения, распределение по синогониям. Вид пространственных решёток кристаллов, установленный впервые французским учёным О. Браве в 1848.Браве высказал гипотезу о том, что пространственные решётки кристаллов построены из закономерно расположенных в пространстве точек — узлов (где расположены атомы), которые могут быть получены в результате повторения данной точки путём параллельных переносов (трансляций (См. Трансляция)) (рис. 1).Проведением прямых линий и плоскостей через эти точки пространственная решётка разбивается на равные параллелепипеды (ячейки). Всего существует 14 видов таких решёток, которыми в первом приближении может быть описана структура любого кристалла. Б. р. делятся на 4 типа (см. рис. 2): 1) примитивный — узлы расположены только в вершинах параллелепипеда, 2) базоцентрированный — имеется ещё по одному узлу в центрах двух противолежащих граней, 3) объёмноцентрированный — к примитивному типу добавлен узел в центре ячейки, 4) гранецентрированный — имеется по одному узлу в центре каждой грани. Б. р. распределяются по сингониям (системам) следующим образом: триклинная — 1, моноклинных — 2, тетрагональных — 2, ромбических — 4, тригональная (ромбоэдрическая) — 1, гексагональная — 1, кубических — 3. 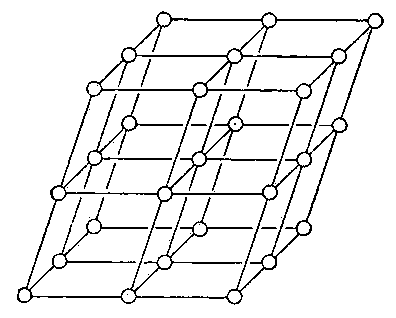 Рис. 1. Схема построения пространственной решётки кристалла путём параллельных переносов. 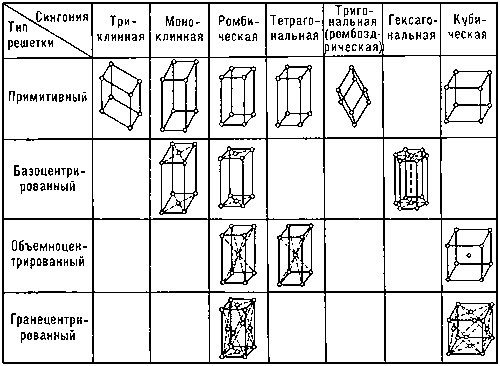 Рис. 2. Решётки Браве. Сингонии: кубическая — куб со сторонами a = b = c и углами между ними α = β = γ = 90°; тетрагональная — параллелепипед a = b ≠ c, α = β = γ = 90°; ромбическая — параллелепипед a ≠ b ≠ c, α = β = γ = 90°; тригональная (ромбоэдр — куб, вытянутый вдоль пространственной диагонали) a = b = c, α = β = γ ≠ 90°; гексагональная — состоит из трех призм с основанием в форме ромба a = b ≠ c, α = β = 90°, γ = 120°; моноклинная — параллелепипед a ≠ b ≠ c, α = γ = 90°, β ≠ 90°; триклинная — косоугольный параллелепипед a ≠ b ≠ c, α ≠ β ≠ γ ≠ 90°. Классы симметрии. Вывод. Формулы и международные символы элементов симметрии. Символика Браве В основном используется в учебных целях и сводится к перечислению всех элементов точечной группы. Поворотные оси симметрии обозначаются буквой L с нижним цифровым индексом n, соответствующим порядку оси ( ) — , , , и . Инверсионные оси (комбинация поворота с инверсией) обозначаются буквой Ł с нижним цифровым индексом n, соответствующим порядку оси (Łn) — Ł2, Ł3, Ł4 и Ł6. Инверсионная ось первого порядка (центр инверсии) обозначается символом C. Инверсионная ось второго порядка есть просто плоскость симметрии и обычно обозначается символом P. Для уточнения ориентации плоскости относительно главной оси могут использоваться разные индексы, например, || и ⊥. Например, символ L2P⊥C обозначает группу, состоящую из оси второго порядка и перпендикулярной к ней плоскости (и, как следствие их взаимодействия, центра инверсии), а символ L22P|| - группу, состоящую из оси второго порядка и двух параллельных ей плоскостей (хотя в случае только параллельных плоскостей символ || обычно опускают и будет L22P). Символ L44L24P||P⊥C обозначает группу, состоящую из оси четвёртого порядка, четырёх перпендикулярных к ней осей второго порядка, четырёх параллельных ей плоскостей, одной перпендикулярной плоскости и центра инверсии. Символ Шёнфлиса Символика Шёнфлиса основана на классификации точечных групп по семействам и широко используется для обозначения вообще всех точечных групп, а не только кристаллографических. Семейство групп с единственной поворотной осью обозначается латинской буквой C с индексом, показываюшим порядок оси. Добавление горизонтальной плоскости к группам Cn обозначается дополнительным индексом h. Добавление вертикальных плоскостей к группам Cn обозначается дополнительным индексом v. Поскольку в группе C1 не существует особых направлений, добавленная плоскость не может характеризоваться как вертикальная или горизонтальная. Такая плоскость обозначается индексом s. Таким образом, символ группы, состоящей из одной плоскости симметрии — Cs. Добавление горизонтальной плоскости к группам Dn обозначается, так же, как и в случае Сn, дополнительным индексом h. Добавление вертикальных плоскостей к группам Dn неоднозначно, так как плоскости могут располагаться как между горизонтальными осями второго порядка, так и совпадать с ними. В первом случае добавляется индекс d, обозначающий диагональное расположение плоскостей (по диагонали между направлениями осей второго порядка). Получаются кристаллографические группы D2d и D3d. В группах Dnd взаимодействие горизонтальных осей второго порядка и вертикальных зеркальных плоскостей приводит к возникновению зеркальной оси порядка 2n. Поэтому группы D4d и D6d не являются кристаллографическими, так как содержат зеркальные оси порядков 8 и 12, соответственно. Добавление к группамDn вертикальных плоскостей вдоль осей второго порядка порождает горизонтальную плоскость симметрии и получаются описанные выше группы Dnh Группы, состоящие из одной зеркальной оси, обозначаются символом Sn. При нечётном n зеркальная ось эквивалентна наличию поворотной оси порядка n и перпендикулярной к ней плоскости, то есть группе Cnh, поэтому в группах Sn индекс n всегда чётный. Кристаллографические точечные группы, в которых присутствуют несколько осей высшего порядка (то есть порядка больше двух), обозначаются символами T или О, в зависимости от присутствующих в них поворотных осей. Дополнительные индексы h и d указывают на наличие горизонтальных (и вертикальных) и диагональных плоскостей симметрии. Если в группе присутствуют только поворотные оси 2 и 3 порядков, то группа обозначается символом T (так как такая комбинация поворотных осей присутствует в тетраэдре). Если в группе присутствуют только поворотные оси 2, 3 и 4 порядков, то группа обозначается символом O (так как такая комбинация поворотных осей присутствует в октаэдре). Добавление горизонтальных плоскостей симметрии приводит к группам Th и Oh (Oh — группа симметрии куба и октаэдра). Обозначения Шёнфлиса используются в теории групп, физике и кристаллографии. В символике Шёнфлиса используются только порождающие элементы симметрии (то есть из которых можно вывести все остальные элементы симметрии группы). Обозначения инвариантны относительно выбора системы координат, что одновременно является как достоинством, когда нас просто интересует симметрия системы, так и недостатком, в случае если важна ориентация элементов симметрии точечной группы по отношению к другим объектам, например, системе координат кристалла, или по отношению к осям решётки Браве пространственной группы. Поэтому в кристаллографии чаще используются символы Германа-Могена, особенно для описания пространственных групп. Символика Германа В символе Германа — Могена обозначаются симметрически неэквивалентные элементы симметрии. Поворотные оси симметрии обозначают арабскими цифрами — 1, 2, 3, 4 и 6. Инверсионные оси обозначают арабскими цифрами с чёрточкой сверху — 1, 3, 4 и 6. При этом ось 2, которая является просто плоскостью симметрии, обозначается символом m (англ. mirror — зеркало). Направлением плоскости является направление перпендикуляра к ней (то есть оси 2). Зеркальные оси в международной символике не используются. Ориентация элемента относительно координатных осей задаётся позицией элемента в символе группы. Если направление оси симметрии совпадает с направлением плоскости, то они записываются на одной позиции в виде дроби. Если инверсионная ось имеет бо́льшую величину симметрии, чем совпадающая с ней поворотная, то в символе указывают именно её (то есть записывают не, а 6; при наличии в группе центра инверсии не 3, а 3). Низшая категория — точечные группы, в которых максимальный порядок любой оси равен 2. К ней относятся группы 1, 1, 2, m, 222, mm2 и. Если в символе группы три позиции, то на 1-й позиции — направление вдоль оси X на 2-й позиции — направление вдоль оси Y на 3-й позиции — направление вдоль оси Z В нестандартной установке группа mm2 может быть записана как m2m или как 2mm. Аналогично, группы 2, m и могут быть записаны более подробно — с указанием, вдоль какой координатной оси идёт направление оси второго порядка и/или плоскости. Например, 11m, 1m1 или m11. Эта особенность символики используется для однозначного описания пространственных групп при различном выборе системы координат, так как символы пространственных групп являются производными от символов соответствующих им точечных групп. Средняя категория — точечные группы, в которых присутствует одна ось порядка выше двух (ось высшего порядка). Тут следует отметить, что в кристаллографии используется кристаллографическая система координат, связанная с симметрией кристалла. В этой системе осями выбираются особые направления в кристалле (направления, вдоль которых идут оси симметрии или трансляции). Поэтому при наличии одной оси 3 или 6 порядка, угол между направлениями X и Y равен 120°, а не 90° как в обычной Декартовой системе координат. на 1-й позиции — направление главной оси, то есть ось Z на 2-й позиции — побочное направление. То есть направление вдоль оси X и эквивалентной ей оси Y на 3-й позиции — диагональное направление между симметрически эквивалентными побочными направлениями К этой категории относятся группы 3, 4, 6, 3, 4, 6, 32, 422, 622, 3m, 4mm, 6mm, 3, 42m, 6m2, и. Поскольку ось 3 и перпендикулярная к ней плоскость эквивалентны оси 6, то = 6 и m2 = 6m2, но использовать рекомендуется именно обозначения с инверсионной осью 6, так как её симметрия выше, чем у оси 3. Группы 42m и 6m2 могут быть записаны как 4m2 и 62m. Выше были приведены обозначения, принятые в русскоязычной литературе. Последовательность символов 2 и m в этих группах становятся важна при описании производных от них пространственных групп, так как элемент на второй позиции направлен вдоль оси ячейки Браве, а элемент на третьей позиции направлен по диагонали грани. Например, символы P42m и P4m2 обозначают две разные пространственные группы. Группа 32 тоже может быть более подробно записана как 321 или 312 для разных ориентаций оси 2. Аналогично, различные ориентации приводят к двум разным пространственным группам P321 и P312. То же относится и к группам 3m (альтернативные записи 3m1 и 31m) и 3 (альтернативные записи 3 1 и 31). Высшая категория — точечные группы, в которых присутствуют несколько осей высшего порядка. на 1-й позиции — эквивалентные направления X, Y, Z на 2-й позиции — всегда присутствующие там четыре оси 3 или 3 на 3-й позиции — диагональное направление между координатными осями К этой категории относятся пять групп — 23, 432, 3, 43m и 3 Международные символы обычно упрощают, заменяя на m, если ось n порождена другими элементами симметрии, указанными в символе. Нельзя убрать лишь обозначение главной оси в средней категории. Например, записывают как mmm, как mm, а 3 как m3m. |
