Сопромат. Заказ 40246.. Отчет удлинения стержня ведем от заделанного края получим Задача Кручение круглого бруса
 Скачать 420.13 Kb. Скачать 420.13 Kb.
|
|
Задание 1. Растяжение-сжатие стержня. Стальной круглый стержень переменного (постоянного) сечения нагружен продольными силами, приложенными на границах обозначения участков. Требуется: Построить эпюру продольных сил 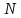 . .Построить эпюру нормальных напряжений в поперечных сечениях. Построить эпюру перемещения сечений относительно заделанного неподвижного торца стержня (сечение I-I). Дано: 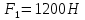 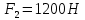 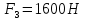 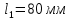 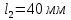 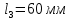 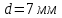 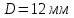 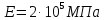 Решение Разобъем стержень на участки и применим метод сечений.За положительное направление продольной силы принимаем направление оси x.  Вычисли площадь поперечного сечения стержня  Строим эпюру продльных сил и нормальных напряжений Учаток I 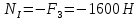 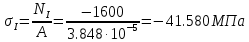 Учаток II  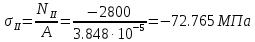 Учаток III 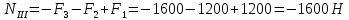 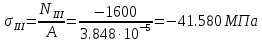 Строим эпюру перемещений. Вычисли для начала удлинение стержня на каждом участке. Участок I 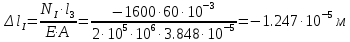 Участок II 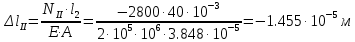 Участок III  Отчет удлинения стержня ведем от заделанного края получим: 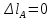 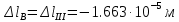 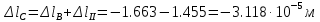  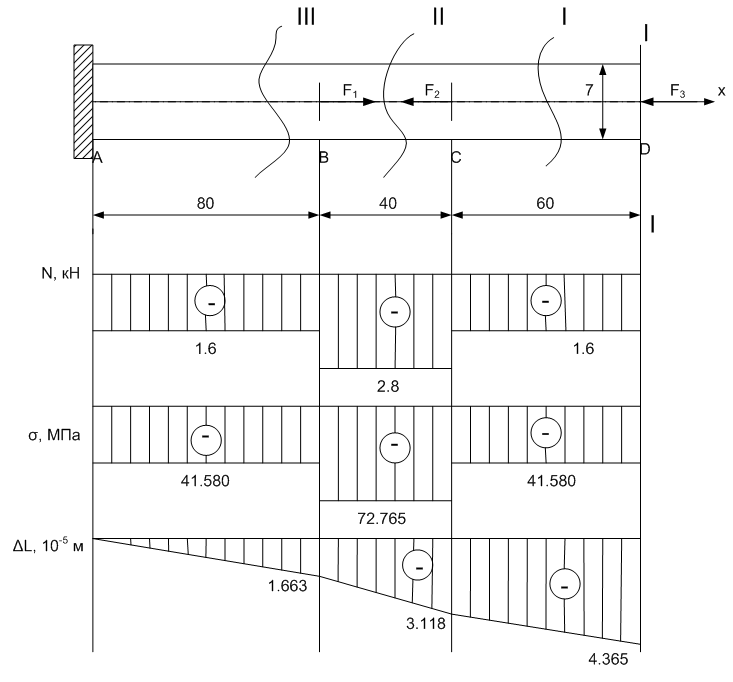 Задача 2. Кручение круглого бруса. К ступенчатому валу, имеющему круглое сплошное поперечное сечение, приложены четыре крутящих момента. Левый конец вала жестко закреплен в опоре, а правый конец – свободен, и его торец имеет угловые перемещения относительно левого конца. Требуется: Построить эпюру крутящих моментов по длине вала. При заданном значении допускаемого напряжения на кручение определить диаметры 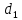 и и 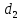 вала из расчета на прочность, полученные значения диаметров округлить согласно ГОСТ 6636-69. вала из расчета на прочность, полученные значения диаметров округлить согласно ГОСТ 6636-69.Построить эпюру действительных напряжений кручения по длине вала. Построить эпюру углов закручивания вала относительно заделанного неподвижного торца вала. Дано: 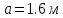 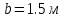 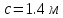 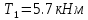 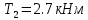 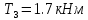 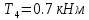 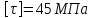 Построим эпюру крутящих моментов.Разобъем вал на участки 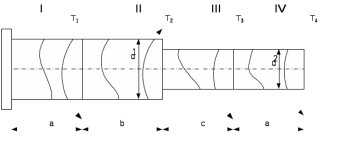 Участок IV  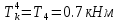 Участок III 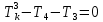 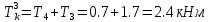 Участок II 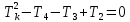  Участок I 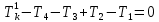 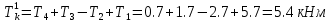 Определим диаметр вала по участкам из условия прочности по формуле: Участок IV 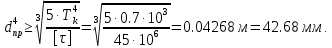 По таблице стандартных значений диаметров валов принимаем 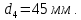 Участок III  По таблице стандартных значений диаметров валов принимаем 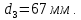 Участок II 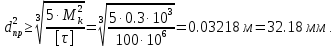 По таблице стандартных значений диаметров валов принимаем 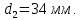 Участок I 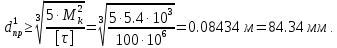 По таблице стандартных значений диаметров валов принимаем 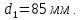 Таким образом имеем согласно рисунку 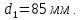 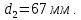 Построим эпюру действительных напряжений кручения по длине вала. Участок IV 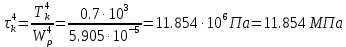 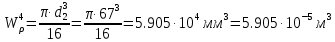 Участок III 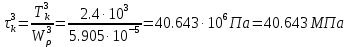  Участок II 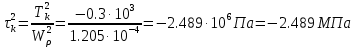 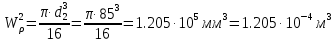 Участок I 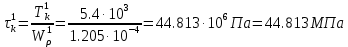 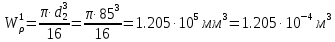 Построим эпюру углов закручивания, считая левый торец вала жестко защемленным. Участок IV Полярный момент инерции. 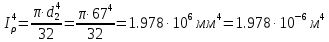 Определим угол закручивания на каждом участке по формуле: 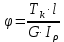 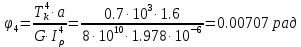 Участок III Полярный момент инерции. 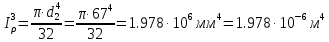 Угол закручивания 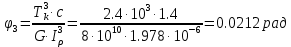 Участок II Полярный момент инерции. 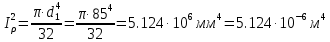 Угол закручивания 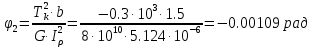 Участок I Полярный момент инерции. 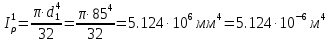 Угол закручивания 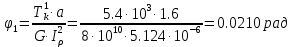 Теперь определим повороты сечений в точках A,B,C,D,E. 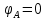     По полученным значениям строим эпюру углов закручивания: 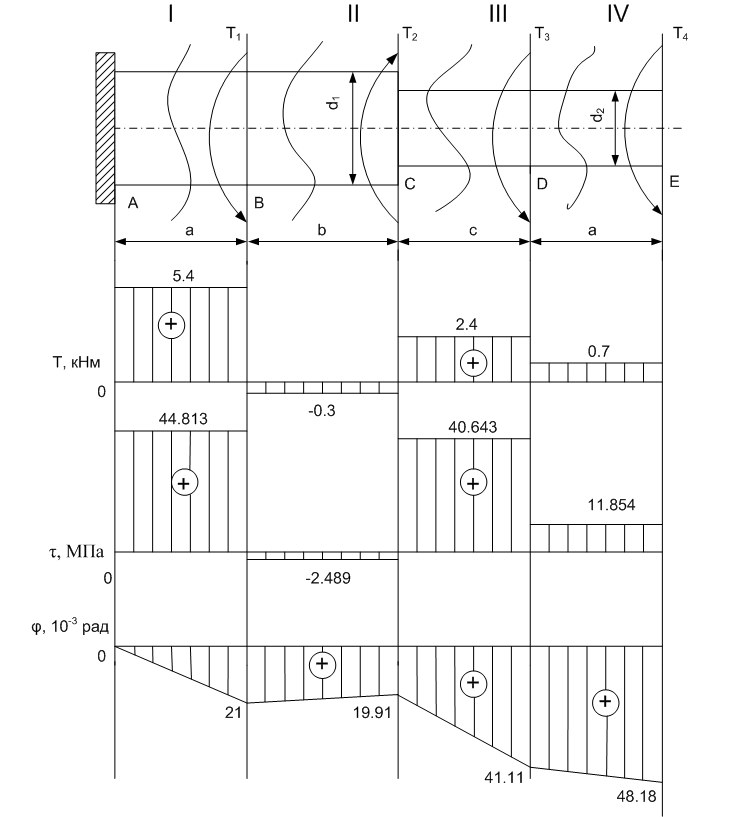 Задача 3. Геометрические характеристики составных плоских сечений. Дана сложная плоская фигура, состаящая из отдельных элементов: полосы, уголка, швеллера, двутавра в комбинации, указанной на рисунке. 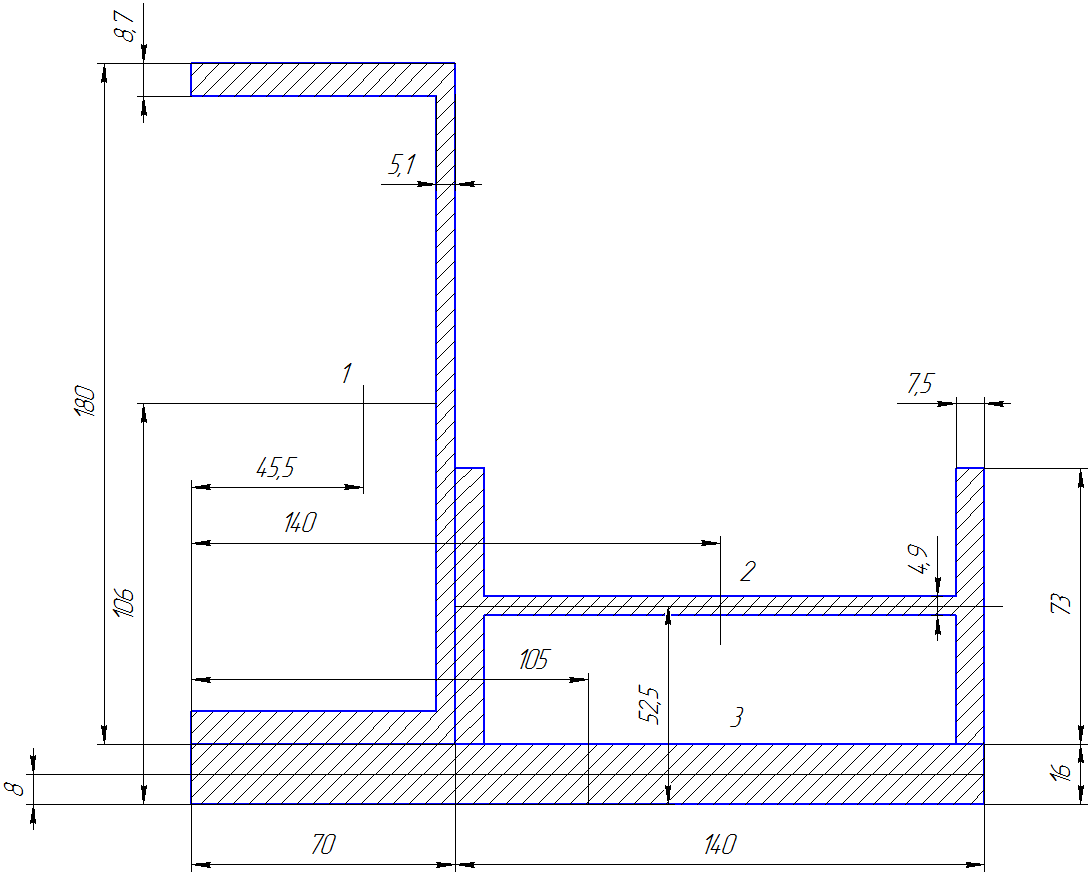 Требуется: Определить положение центра тяжести заданного составного сечения. Вычислить осевые и центробежные моменты инерции площади отдельных элементов и всей заданной фигуры относительно вспомогательных осей составного сечения. Определить положение главных центральных осей всей площади. Вычислить величины главных центральных моментов инерции. Выполнить чертеж фигуры на формате А4 или А3 в натуральную величину в соответствии с требованиями ЕСКД с указанием центров тяжестей элементов и всей фигуры и всех используемых систем координат. Дано: Номер двутавра 14, номер швеллера 18, номер уголка 8, толщина полосы 16 мм. По таблице сортамента для швеллера находим: 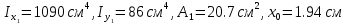 Из чертежа имеем координаты центра тяжести швеллера: 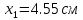  По таблице сортамента для двутавра находим: 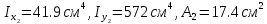 Из чертежа имеем координаты центра тяжести двутавра: 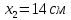 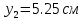 Для полосы находим: 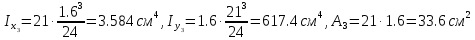 Из чертежа имеем координаты центра тяжести полосы: 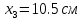 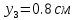 Находим координаты центра инерции составного сечения для этого введем оси x,y как показано на чертеже: 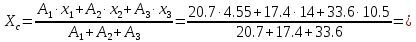 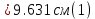 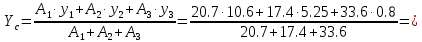 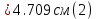 Проводим через центр инерции сечения оси  . .Находим моменты инерции сечения относительно осей 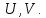 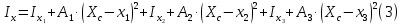 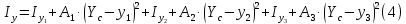 Соответствующие значения 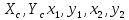 берем из (1),(2). берем из (1),(2).Подставляя в (3), (4) числовые значения получим: 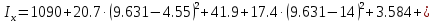 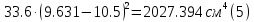 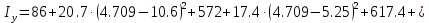 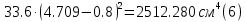 Находим значение центробежного момента всего сечения: 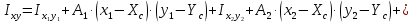 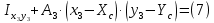 Подставляя в (7) числовые значения получим: 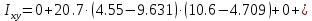 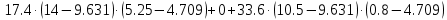  Вычисляем главные моменты инерции всего сечения: 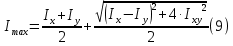 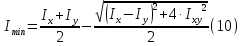 Подставляя в (9) и (10) числовые значения получим:  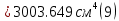 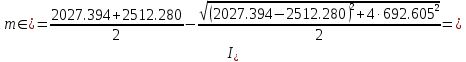 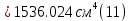 Находим положение главных осей инерции по формуле: 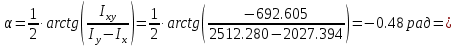 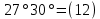 Изобразим на чертеже главные оси Y,X.  Задача 4. Расчет статически неопределимых стержневых систем. Дана статически неопределимая стержневая система Требуется: Определить усилия в стержнях. Вычислить реакции связей в шарнирных опорах. Найти площади сечений стержней, удовлетворяющих условию прочности. Допускаемое напряжение для всех вариантов принять 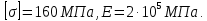 Дано: 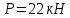 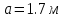 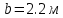   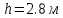 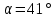 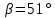 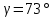 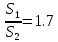 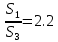 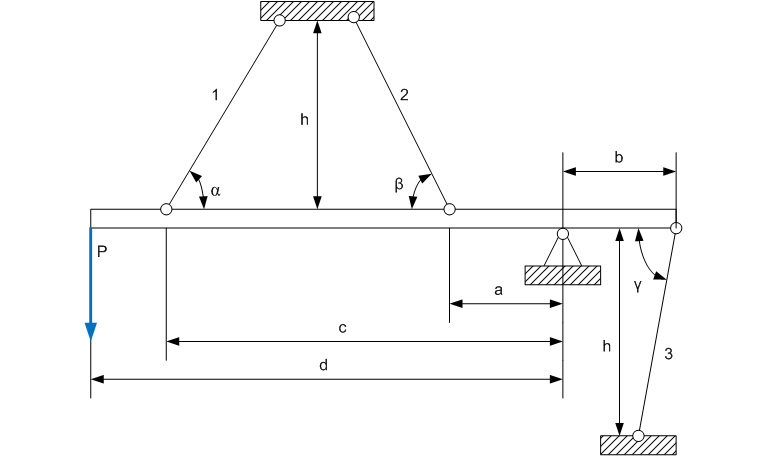 Решение Придадим стержню элементарное перемещение в направлении действия силы так как показано на рис. ниже. 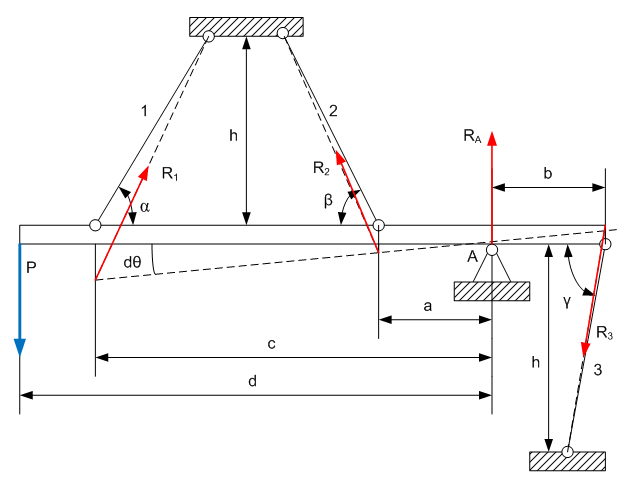 Тогда элементарное приращение длин стержней равно: 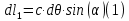 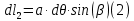 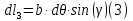 Силы действующие в поперечных сечениях стержней будут равны: 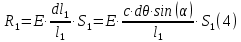 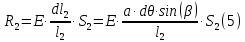 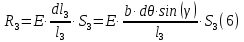 Составим уравнение моментов сил для точки А.  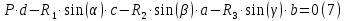 Подставляя в (7) (4),(5),(6) получим: 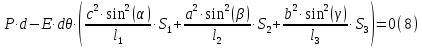 Из рисунка видно что: 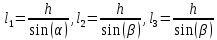 Тогда (8) преобразуется к виду: 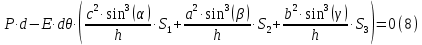 Из выражения (8) находим 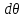 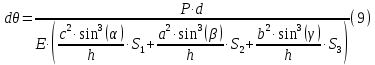 Подставляя (9) в (4),(5),(6) и получим:  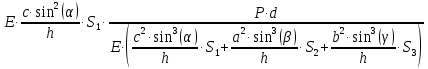 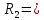 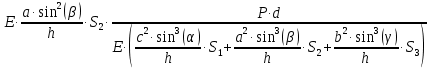 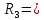 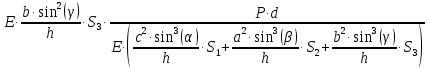 Делая дальнейшие упрощения получим: 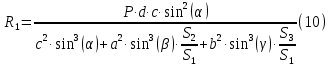 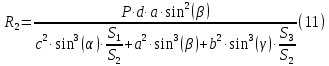  Подставляя в (10),(11),(12) числовые значения получим:  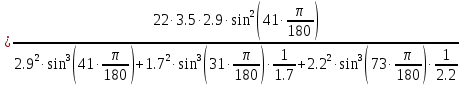 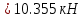 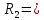 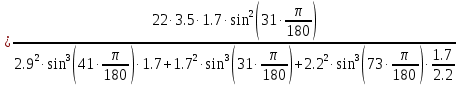 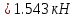 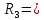 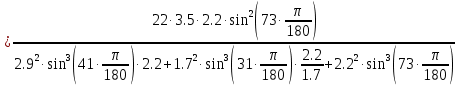  Найдем площади сечений стержней удовлетворяющие условию прочности. Согласно закону Гука имеем: 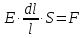 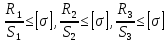 Отсюда имеем: 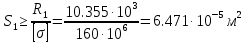 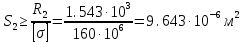 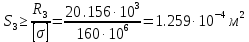 Задача 5. Изгиб балки, подбор поперечного сечения. Дана балка нагруженная как показано на рис. (схема 1)Числовые данные к расчету приведены, 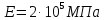 . .Требуется подобрать балку прямоугольного поперечного сечения 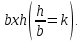 Дано: 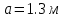   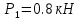 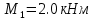 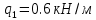 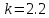 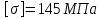 Схема 1 Решение Определим сначала реакции опор. 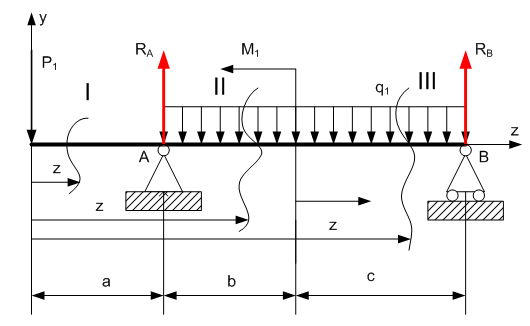 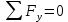    Из (2) следует: 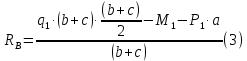 Подставляя в (3) числовые значения получим: 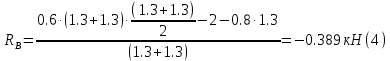 Из (1) следует: 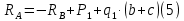 Подставляя в (5) числовые значения получим: 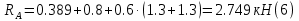 Составим аналитические выражения изгибающего момента 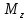 Участок I: 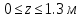 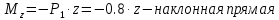 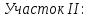 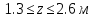 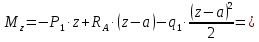 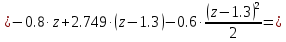  Найдем вершину параболы: 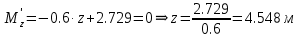 Вершина лежит вне участка. 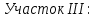 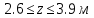  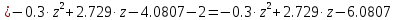  Построим эпюру изгибающих моментов 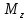 Участок I: 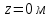  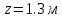 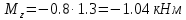   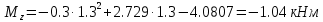 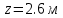 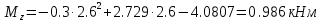  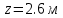 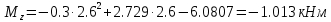 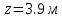 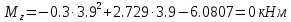 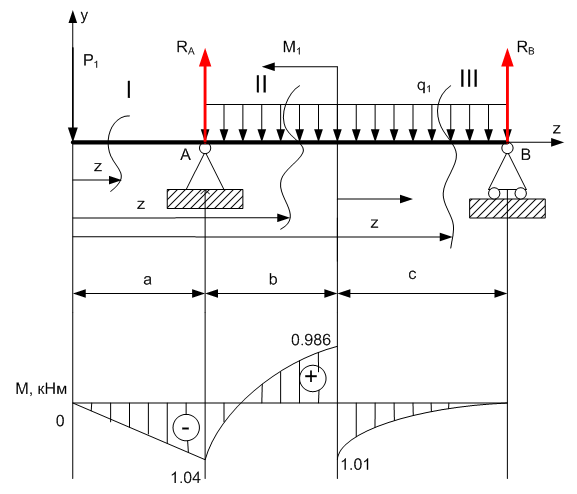 По эпюре изгибающих моментов определяем опасную точку – это точка A. Запишем условие прочности 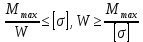 По условию 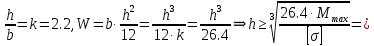 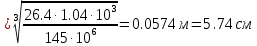 Принимаем  Принимаем 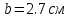 Задача 6. Подбор сечения балки и полная проверка ее на прочность. Дана балка, загруженная как указано на рис. (схема 2) Числовые данные к расчету приведены 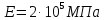 . . Требуется подобрать балку двутаврового сечения и выполнить полную проверку ее на прочность. Дано: 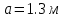   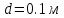 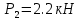 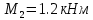  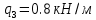 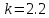 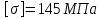 Определим сначала реакции опор 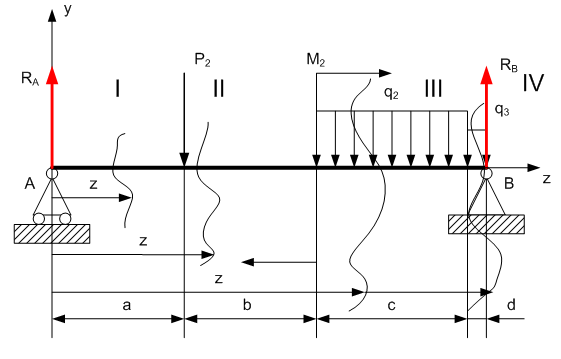 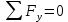 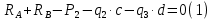  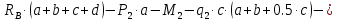 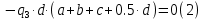 Из (2) следует:  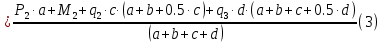 Подставляя в (3) числовые значения получим: 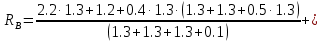  Из (1) следует: 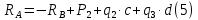 Подставляя в (5) числовые значения получим:  Составим аналитические выражения изгибающего момента 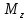 Участок I:   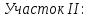 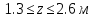 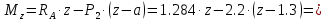 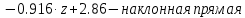  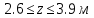 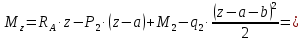 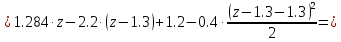 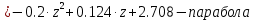 Найдем вершину параболы: 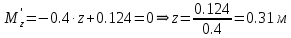 Вершина лежит вне участка.  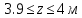  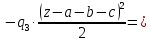 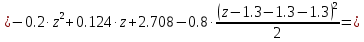 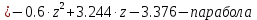 Найдем вершину параболы: 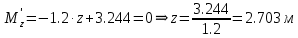 Вершина лежит вне участка. Построим эпюру изгибающих моментов  Участок I:   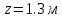 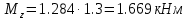   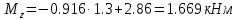  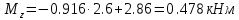  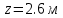 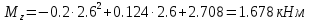 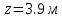 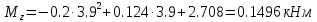  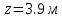 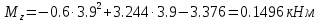 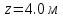 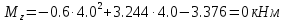 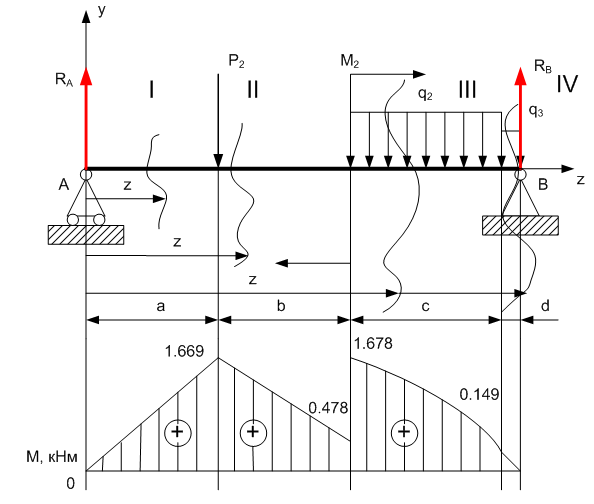 По эпюре изгибающих моментов определяем опасную точку. Запишем условие прочности 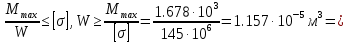 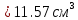 По ГОСТ 8239-89 принимкаем двутавр 10   Задача 7. Определение перемещений в балках при плоском изгибе. Дана балка, нагруженная как указано на рис. (схема 2). Числовые данные к расчету приведены.  . .Требуется: Используя расчеты предыдущего раздела, составить уравнение изогнутой оси балки. Определить значения прогибов балки в точках 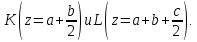 Определить значения углов поворота сечений в точках 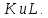 Решение  Необходимо определить прогибы и углы поворота сечений в точках. 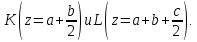 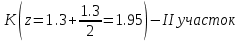 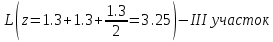 Записываем уравнение изогнутой оси балки:  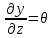 Для I участка имеем: 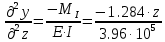  Определяем угол прогиба на первом участке:  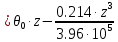 Для II участка имеем:  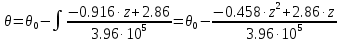 Определяем угол прогиба на втором участке: 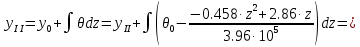 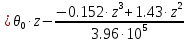 Для III участка имеем:  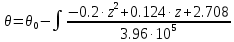 Определяем угол прогиба на третьем участке: 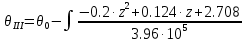 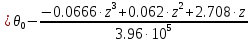 Определим прогиб на третьем участке:  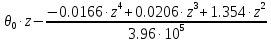 Для IV участка имеем: 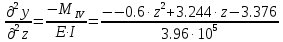 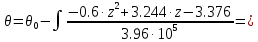 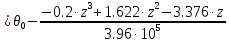 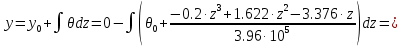 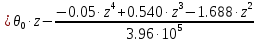 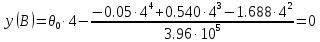 Отсюда находим: 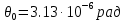 Определим прогиб в точках K и L. 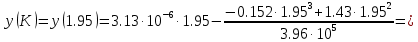 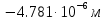 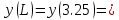 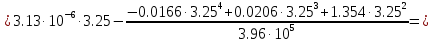  |
