ПЕРЕДАЧА ФУНКЦИЙ В КАЧЕСТВЕ ПАРАМЕТРОВ. ПЕРЕГРУЗКА ФУНКЦИЙ. 4218_Ситников_Артём_Витальевич_ОП_ЛР1. Отчет защищен с оценкой преподаватель ассистент
 Скачать 86.66 Kb. Скачать 86.66 Kb.
|
|
ГУАП КАФЕДРА № 44 ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ ПРЕПОДАВАТЕЛЬ
РАБОТУ ВЫПОЛНИЛ
Санкт-Петербург 2023 Основная часть Вариант 26: y = x2; y = 4x – x2 Описание выбранного решения: Площадь фигуры, образованной двумя линиями равна разнице определённых интегралов каждой функции на отрезке [a, b], где a и b – нижний и верхний пределы интегрирования. Для нахождения определённого интеграла была реализована функция, использующая метод Симпсона. Точки пересечения между графиками функций и пересечения каждой функции с осью 0х находятся при помощи перегруженных функций, перебирающих значения в диапазоне с маленьким шагом с помощью цикла. Когда ищутся точки пересечения с осью 0х, значение функции в определённой точке сравнивается с величиной шага. Если значение функции меньше, точки добавляются в массив, а затем вычисляется среднее значение. Если нужно найти пересечение между двумя функции, то идет сравнение разницы значений функций в точке с величиной шага. Исходный код: main.cpp: #include "Header.h"//подключение заголовочного файла с подключением модулей и объявлением функций using namespace std; //функции нахождения точек пересечения прописаны в основном файле, так как при выносе в отдельный файл не подключается vector vector vector float(*func1)(float), float(*func2)(float));//точки пересечения двух функций int main() { vector //массив с точками пересечения функций cout << "Intersection points: "; for (int i = 0; i < data.size(); i++) { cout << data.at(i) << ' ';//вывод точек пересечения } cout << endl; double square = abs(simpsons_(data.at(0), data.at(1), 10, func1)\ - simpsons_(data.at(0), data.at(1), 10, func2));\ //нахождение площади cout << "Square = " << square; return 0; } vector float(*func)(float)) { vector //массив со значениями, при которых значение функции находится в допустимых пределах от 0 vector for (double i = -200.0; i <= 200; i = i + step)\ //перебираем значения x с определенным шагом, влияющим на количество точек в arr { if (abs(func(i)) <= step)\ //проверка на нахождение в допустимом пределе arr.push_back(i); } //далее нахожу средние арифметические всех точек вблизи "настоящей точки" и таким образом нахожу примерное значение точек пересечения //при этом округляю значения до n-ого знака после запятой int count = 1; double summ = arr.at(0); for (int i = 1; i < arr.size(); i++) { if (arr.at(i) - arr.at(i - 1) <= step * 2.0) { summ += arr.at(i); count++; } else { result.push_back(round(summ / count *\ pow(10, rounding_to_n_sign)) / pow(10, rounding_to_n_sign)); count = 1; summ = arr.at(i); } } result.push_back(round(summ / count * pow(10, rounding_to_n_sign)) / pow(10, rounding_to_n_sign)); return result; } vector { vector vector for (double i = -200.0; i <= 200; i = i + step) { if (abs(func1(i) - func2(i)) <= step) arr.push_back(i); } int count = 1; double summ = arr.at(0); for (int i = 1; i < arr.size(); i++) { if (arr.at(i) - arr.at(i - 1) <= step * 2.0) { summ += arr.at(i); count++; } else { result.push_back(round(summ / count *\ pow(10, rounding_to_n_sign)) / pow(10, rounding_to_n_sign)); count = 1; summ = arr.at(i); } } result.push_back(round(summ / count * pow(10, rounding_to_n_sign))\ / pow(10, rounding_to_n_sign)); return result; } functions.cpp #include float func1(float x) { return pow(x, 2) } float func2(float x) { return 4 * x - pow(x, 2); } #include using namespace std; simpsons.cpp float simpsons_(float ll, float ul, int n, float(*func)(float)) { // Calculating the value of h float h = (ul - ll) / n; // Array for storing value of x and f(x) float x[10], fx[10]; // Calculating values of x and f(x) for (int i = 0; i <= n; i++) { x[i] = ll + i * h; fx[i] = func(x[i]); } // Calculating result float res = 0; for (int i = 0; i <= n; i++) { if (i == 0 || i == n) res += fx[i]; else if (i % 2 != 0) res += 4 * fx[i]; else res += 2 * fx[i]; } res = res * (h / 3); return res; } Header.h #pragma once #include #include #include int add(int x, int y); float func(float x); float func1(float x); float func2(float x); float simpsons_(float ll, float ul, int n, float(*func)(float)); Результат работы программы:  Рисунок 1 – Результат работы программы Аналитическое решение: 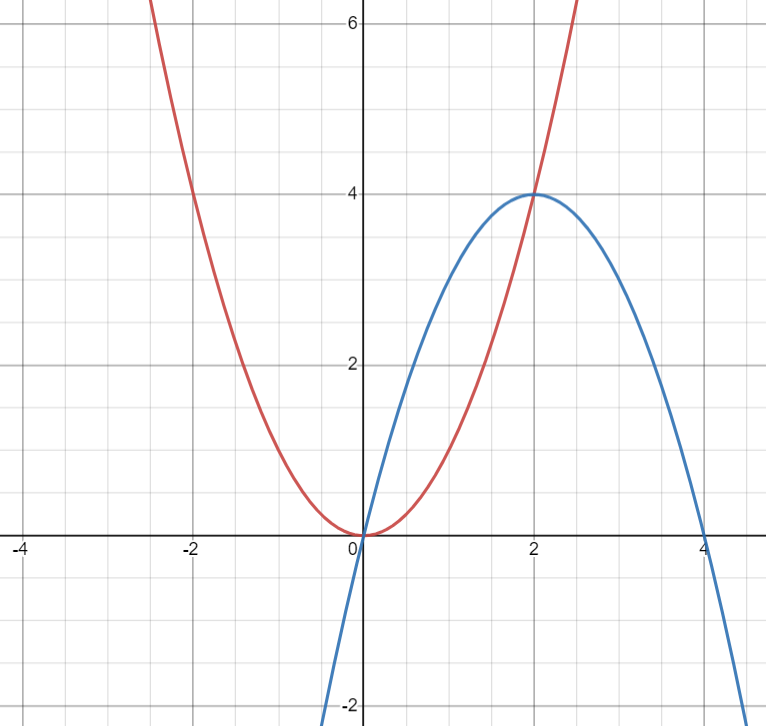 Рисунок 2 – График функции 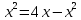 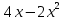 x = 0;2 – точки пересечения функций 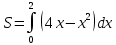 = 2,(6) = 2,(6)Вывод: Результаты работы программы совпадают с результатами аналитического решения в рамках погрешности. Ссылка на GitHub: https://github.com/Temis010/Proba.new/tree/main/training_labs |
