Разбор задачи. практическая работа. Решение Рассмотрим функции у и у. Найдем точки пересечения графиков данных функций
 Скачать 426.89 Kb. Скачать 426.89 Kb.
|
|
Задачи с параметром. Найдите все значения a, при каждом из которых уравнение | 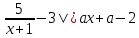 на промежутке (- 1; + 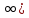 имеет больше двух корней. имеет больше двух корней.Решение : Рассмотрим функции . у= 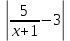 и у= и у= 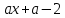 . Найдем точки пересечения графиков данных функций. . Найдем точки пересечения графиков данных функций. Определим, при каких a графики будут иметь более двух общих точек на промежутке (- 1; + 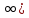 . . Уравнение у= а( х+1) задает семейство прямых, проходящих через точку (-1; 0) с угловым коэффициентом, равным a. Изобразим эскиз графика функции f (заметим, что при а 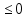 графики не имеют общих точек на промежутке (- 1; + графики не имеют общих точек на промежутке (- 1; + 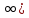 . .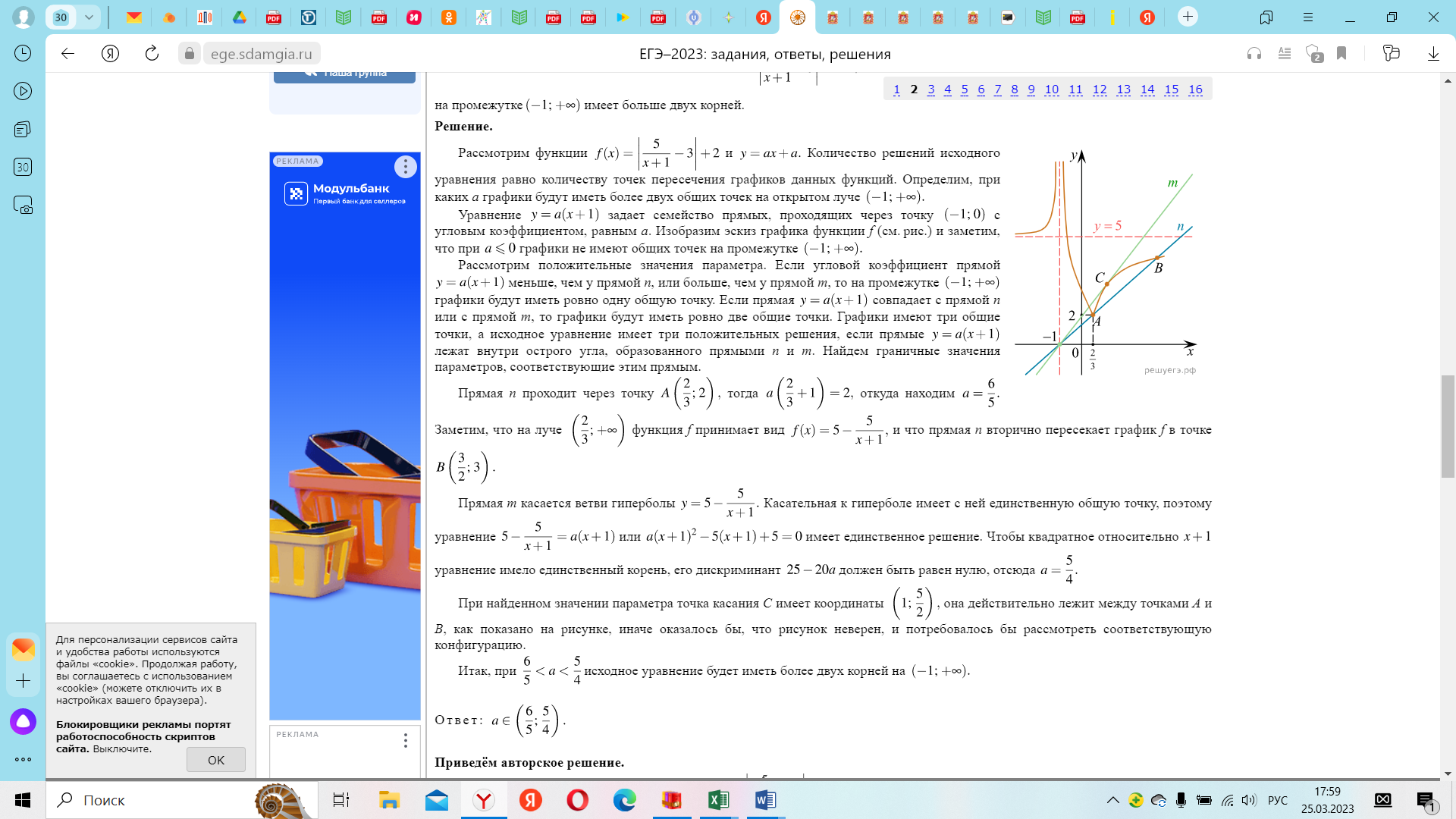 Рассмотрим положительные значения параметра. Если угловой коэффициент прямой у= а( х+1) меньше, чем у прямой n, или больше, чем у прямой m, то на промежутке (- 1; + 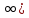 графики будут иметь ровно одну общую точку. графики будут иметь ровно одну общую точку. Если прямая у= а( х+1) совпадает с прямой nили с прямой m, то графики будут иметь ровно две общие точки. Графики имеют три общие точки, а исходное уравнение имеет три положительных решения, если прямые у= а( х+1) лежат внутри острого угла, образованного прямыми nиm. Найдем граничные значения параметров, соответствующие этим прямым.  Прямая n проходит через точку A ( Прямая n проходит через точку A ( 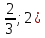 тогда a ( тогда a (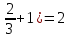 a= a= 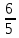 . . На промежутке ( 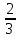 ; + ; + 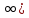 функция f функция f  принимает вид f (х)=5+ принимает вид f (х)=5+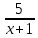 и прямая n вторично пересекает график f в точке В ( и прямая n вторично пересекает график f в точке В (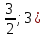 Прямая m касается ветви гиперболы f (х)=5- 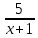 .Касательная к гиперболе имеет с ней единственную общую точку, поэтому уравнение 5- .Касательная к гиперболе имеет с ней единственную общую точку, поэтому уравнение 5- 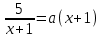 имеет единственное решение. имеет единственное решение. Чтобы квадратное уравнение а(х+1)2 -5 (х+1)+5=0 имело единственный корень, его дискриминант D=25- 20а = 0 , тогда а= 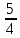 . .При найденном значении параметра точка касания С имеет координаты С(1; 2,5), она лежит между точками A и B, как показано на рисунке. при 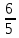 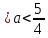 исходное уравнение будет иметь более двух корней на (- 1; + исходное уравнение будет иметь более двух корней на (- 1; + 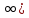 Ответ: а 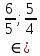 ) ) |
