МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ВЗАИМОДЕЙСТВИЯ ДВУХ ПОПУЛЯЦИЙ «ХИЩНИК-ЖЕРТВА. Отчет защищен с оценкой преподаватель доц., к т. н

• Название: Отчет защищен с оценкой преподаватель доц., к т. н
• Анкор: МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ВЗАИМОДЕЙСТВИЯ ДВУХ ПОПУЛЯЦИЙ «ХИЩНИК-ЖЕРТВА
• Дата: 02.12.2021
• Размер: 0.89 Mb.
• Имя файла: Otchet_2.docx
• Тип: Отчет; #289415

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное автономное образовательное учреждение
высшего образования

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»

КАФЕДРА ИННОВАТИКИ И ИНТЕГРИРОВАННЫХ СИСТЕМ КАЧЕСТВА
ОТЧЕТ
ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

доц., к.т.н.				А.В. Епифанов
должность, уч. степень, звание		подпись, дата		инициалы, фамилия
ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ «МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ВЗАИМОДЕЙСТВИЯ ДВУХ ПОПУЛЯЦИЙ «ХИЩНИК-ЖЕРТВА»»
по дисциплине: МОДЕЛИРОВАНИЕ ПРИРОДНЫХ И ТЕХНИЧЕСКИХ ПРОЦЕССОВ

РАБОТУ
ВЫПОЛНИЛА

СТУДЕНТКА ГР.	М656				Г.К. Осипова М. В. Костылева
			подпись, дата		инициалы, фамилия

Санкт-Петербург 2019

Цель работы: построить математическую модель «хищник-жертва», найти точку бифуркации.

Задачи:

• 
  Построить математическую модель «лиса-заяц»;
  
• 
  Построить графики зависимости численности лис от численности зайцев, изменения численности лис и численности зайцев от времени;
  
• 
  Найти точку бифуркации.
  

Ход работы:

1. 
   Исходные данные: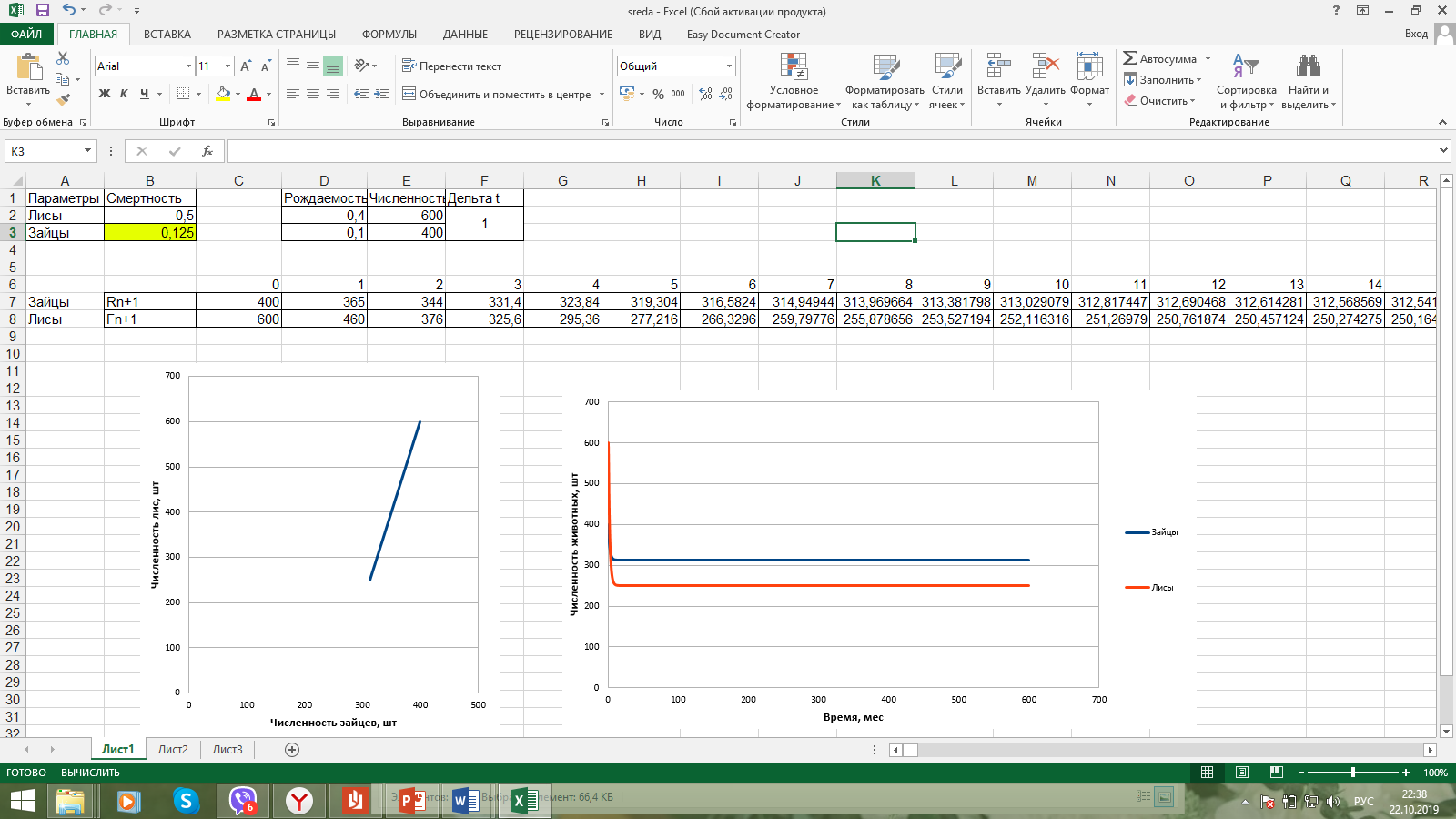
   

2. 
   Математическая модель изменения численности животных: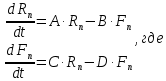
   

R_n – численность зайцев в n-ый момент времени, F_n – численность лис в n-ый момент времени, А – это коэффициент, характеризующий рождаемость зайцев, В – смертность зайцев, С – рождаемость лис, D – смертность лис.

Выразив из математической модели: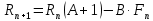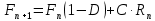





Можем вычислить численность популяции лис и зайцев в каждом новом месяце: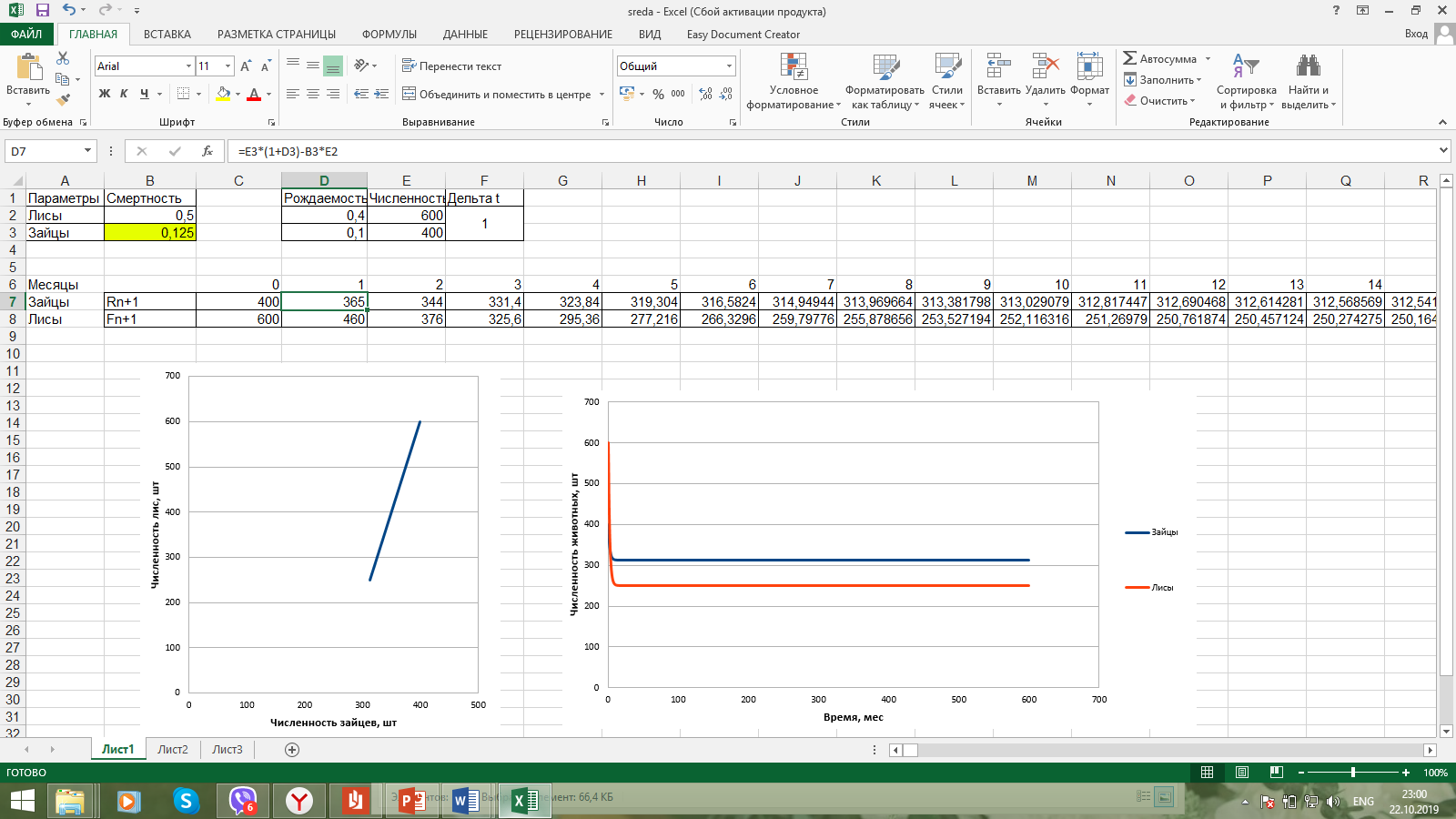

2. 
   Построим графики зависимости численности лис от численности зайцев, изменения численности лис и численности зайцев от времени: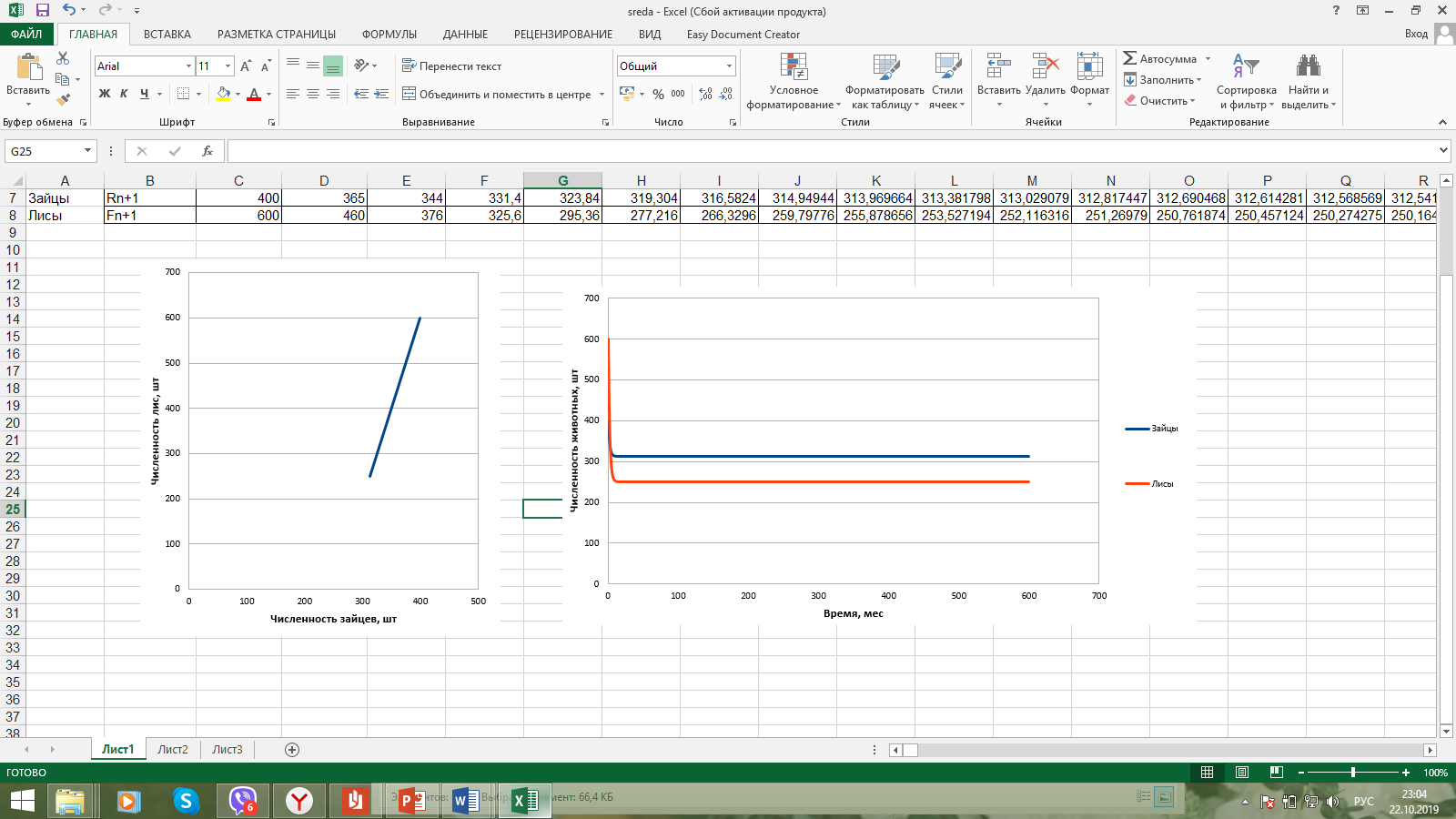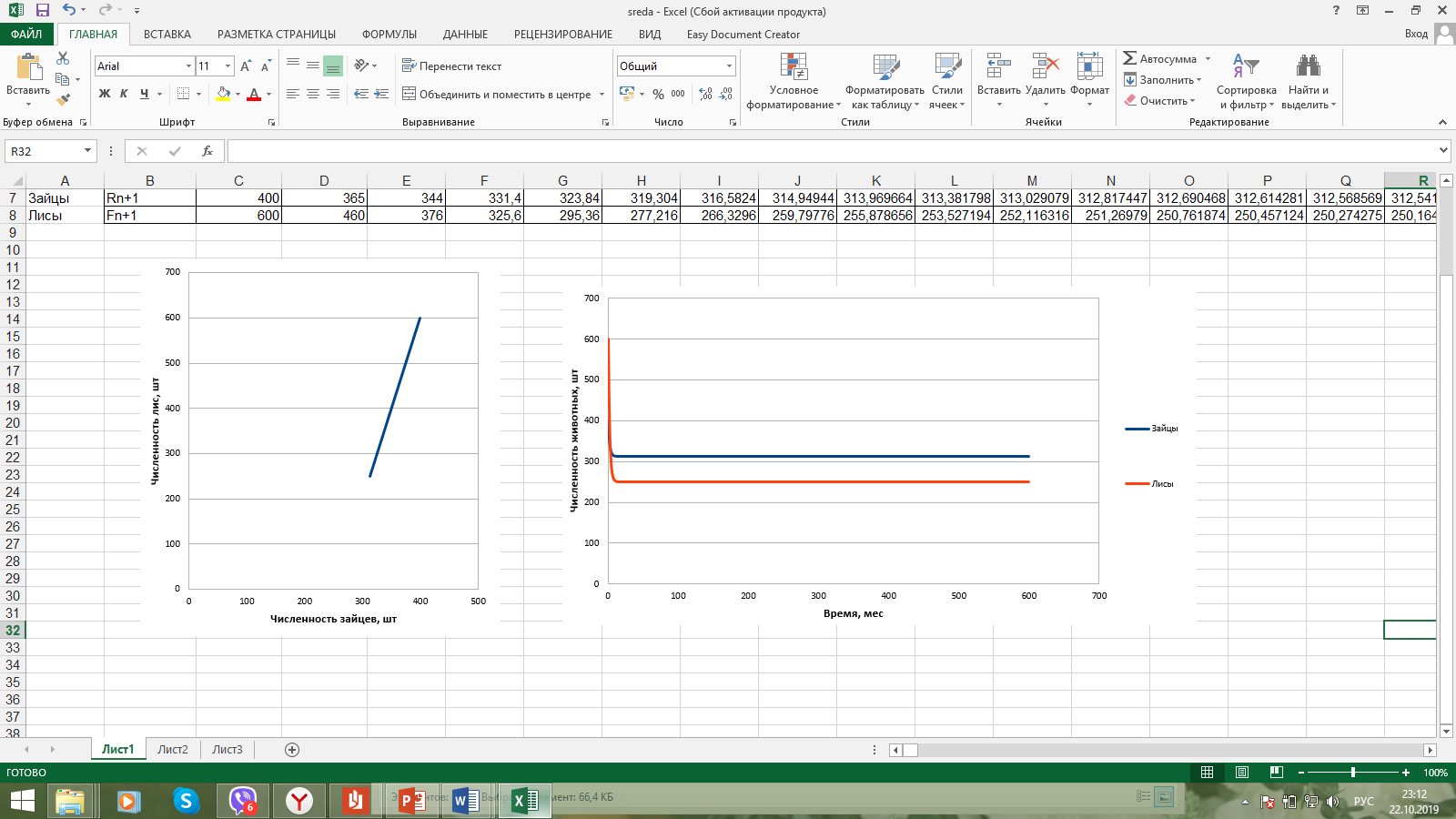
   

2. 
   Методом подбора определим точку бифуркации, то есть, изменяя коэффициент смертности зайцев, найдем такой, при котором система обретет равновесие. Точка бифуркации обнаруживается при В=0,125.
   

Докажем это математически: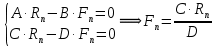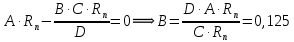





Также, изменив коэффициент на графике увидим, что система теряет равновесие:

При В=0,13 численность популяции уменьшается: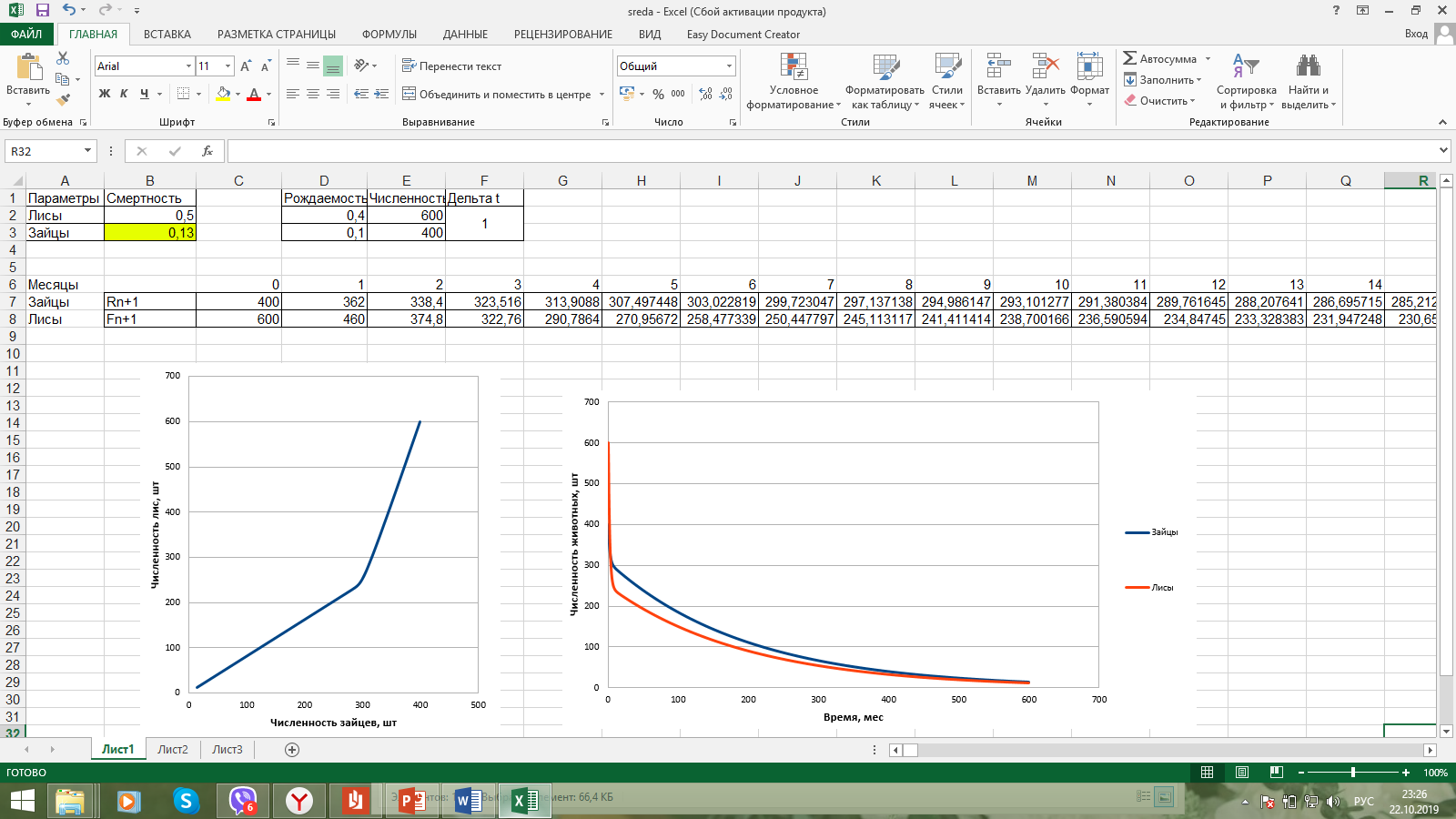



При В=0,12 численность популяции бесконечно увеличивается: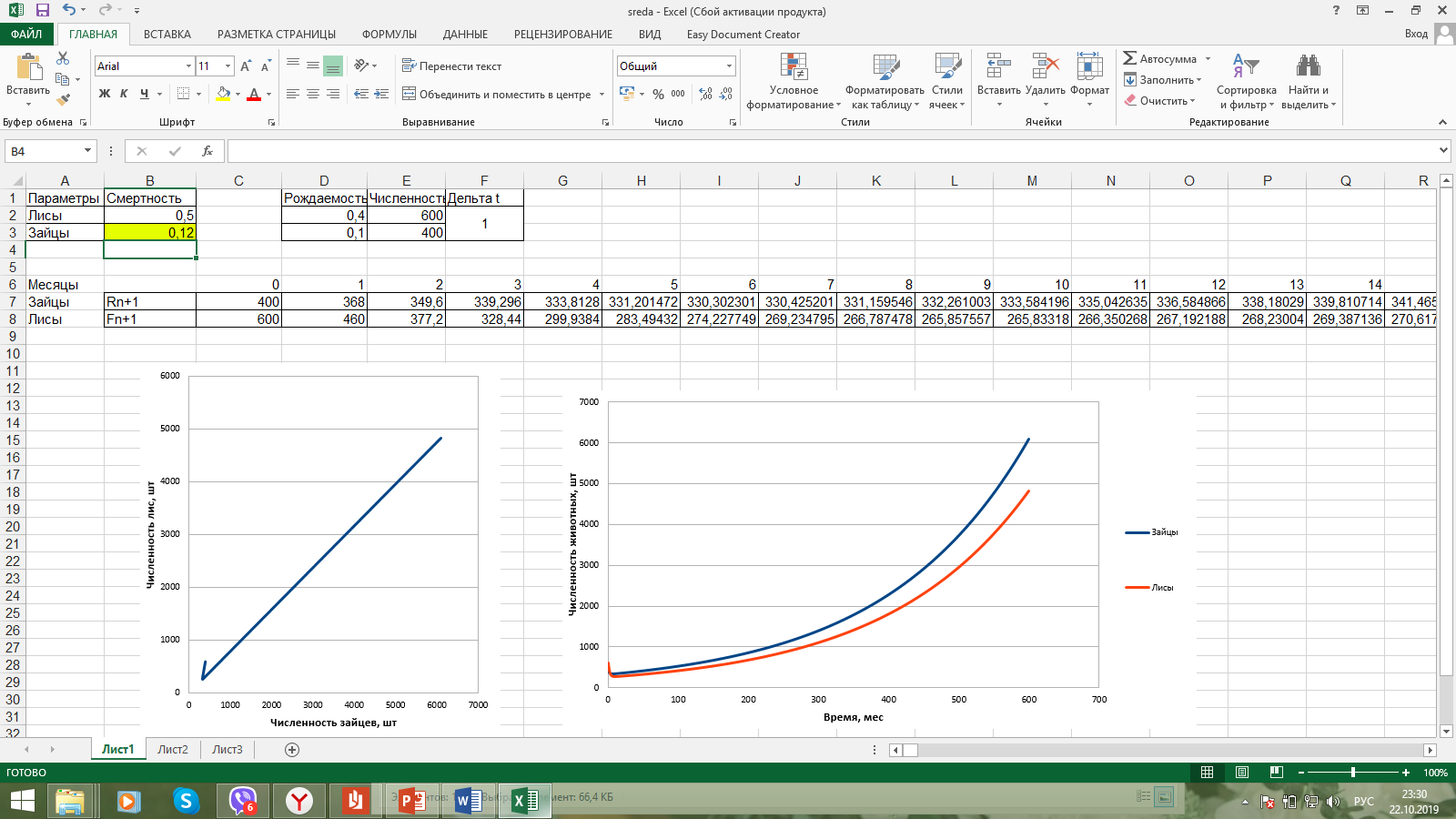



Вывод: В ходе выполнения лабораторной работы построена математическая модель «хищник-жертва», найдена точка бифуркации при В=0,125.