физика. Отсчета

• Название: Отсчета
• Анкор: физика
• Дата: 21.02.2022
• Размер: 2.35 Mb.
• Имя файла: mashinka.docx
• Тип: Документы; #369337
• страница: 1 из 3

1. Модели механики. Система отсчета.

Модели механики:

1) материальная точка- это тело размерим которого можно пренебречь

2) система материальных точек-несколько материальных точек

3) абсолютно твёрдое тело- это тело, расстояние между точками которого не меняется

Движение абсолютно твёрдого тела можно описать поступальным движением, и вращательным.

Поступательное движение- называют движение при котором прямая, соединяющая две произвольные его точки остаются параллельными при перемещении.

Вращательное- движение тела вокруг неподвижно оси, все точки описывают круг и находятся постоянно на одной прямой перпендикулярной к центру оси вращения.

Система отсчёта:

x, y, z- точки которые описывают положение тела в пространстве. Иначе их можно записать вектором r=xi(вектор)+yj(вектор)+zk(вектор). СИ= 1 метр.

В этой системе отсчёта есть часы СИ t=1c.

С 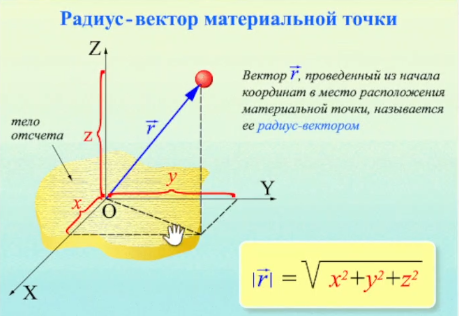истема отсчёта:

Телом отсчёта- называется произвольно выбранное тело относительно которого производится расчёт.

Система отчёта- совокупность системы координат и часов, связанных с телом отсчёта.

зная функции мы можем подставить их в эти уравнения и узнать координату в любой момент времени.

(дельта r вектор) Перемещение- это вектор дельта r(вектор) связывающий начальную и конечную точку пути. Модуль перемещения- это кратчайшее расстояние.

(S)Путь- это расстояние, пройдённое точкой вдоль траектории. Путь всегда больше перемещения по модулю.

2. Скорость материальной точки.

Есть средняя скорость по модулю(по пути) . При равномерном движении.

При неравномерном движении- мгновенная скорость.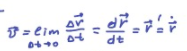

Скорость через вектор измеряется в СИ м/с.

Если скорость постоянна- то это равномерное движение .

Если скорость зависит от времени то графический способ нахождения пути- .

3. Ускорение материальной точки.

Ускорение- быстрота измерения скорости.



П 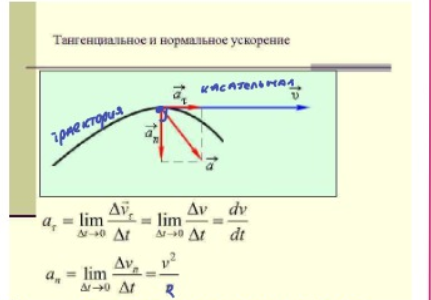одвижная система отсчёта:





Е сли R (радиус движения)постоянно то движение идёт по окружности.

Е сли постоянно тангенсальное ускорение(а) то движение равнперемено.

Путь при равнопеременном движении.



Тангенсальная составляющая ускорения характерезует быстроту измерения скорости по модулю(направлена по касательной к траектории).

Нормальная состовляющая ускорения – быстроту изменения скорости по направлению(направлена к центру кривизны траектории).

4. Кинематика вращательного движения.

Вращение точки вокруг оси вращения головки винта подчиняется правилу правого винта.

Векторы направления которых связываются с направлением вращения называются псевдовекторами или аксильными векторами.Эти векторы не имеют определённых точек и могут откладываться от любой точки оси вращения.

Угловой скоростью называется векторная величина, определяемая первой производной угла поворота тела по времени: .

Линейная скорость точки:

Если угловая скорость постоянная, то это является периодом вращения T .

Число полных оборотов за единицу времени является частотой вращения .

Угловое ускорение это величина описывающая увеличение угловой скорости со временем. Находится как производная от угловой скорости к производной от времени . При вращении тела вокруг оси вектор углового ускорения при постоянной скорости направлен вдоль . При ускоренном движении сонаправлен вектору ускорения. При замедленном- противонаправлен.

Связь между линейными и угловыми величинами выражается через эти формулы .

В случае движения по окружности .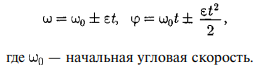

Кинетическая энергия при вращательном движении

5. Законы Ньютона.

Первый закон ньютона гласит- всякая материальная точка(тело) сохраняет своё состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит её изменить это состояние. Стремление тела сохранять это состояние называется его инертностью. Иначе Первый закон ньютона называют законом инерции.

Инерциальные системы отсчёта- это те системы в которых выполняется первый закон ньютона. В таких системах тело либо покоится, либо движется равномерно и прямолинейно. Первый закон ньютона утверждает существование таких систем отсчёта.

Пример: звёздная система(начало координат в центре солнца).

Масса тела- физическая величина, являющаяся одной из основынх харакеристик тела, опроделяющие её инерциональные и гравитационные свойства.

Сила- векторная величина, измеряющая механическое воздействие на тело другими телами в результате которого у тела меняется ускорение, форма, размеры.

Второй закон ньютона- ускорение приобретаемое телом прямо пропорционально вызывающей его силе, совпадает с нею по направлению и обратно пропорционально массе тела. ; уравнение движени материальной точки - общая формулировка второго закона Ньютона. Сила измеряется в ньютонах(Н)= 1 кг*м/см^2.

Второй закон ньютона справедлив только в инерциональных системах отсчёта.

- тангенсальная сила; - нормальная сила.

Третий закон Ньютона:

Любое действие матереальных точке друг на друга носит характер взаимодействия. Силы, с которыми точки действуют друг на друга, равны по модулю и противоположны по направлению в доль соединяющих их прямой .

6. Закон всемирного тяготения. Сила тяжести.

Закон всемирного тяготения: между любыми двумя материальными точками действует сила взаимного притяжения, прямо пропорциональная произведению масс этих точек (м1 и м2) и обратно пропорциональная квадрату расстояния между ними (r^2).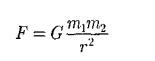



Эта сила называется гравитационной (или силой всемирного тяготения). Силы тяготения всегда являются силами притяжения и направлены вдоль прямой, проходящей через взаимодействующие тела. Коэффициент пропорциональности G называется гравитационной постоянной. G = 6,67*10^-11
Вблизи поверхности Земли все тела падают с одинаковым ускорением, которое получило название ускорения свободного падения g. Таким образом, в системе отсчета, связанной с Землей, на всякое тело массой м действует сила, называемая силой тяжести.



Согласно фундаментальному физическому закону — обобщенному закону Галилея, все тела в одном и том же поле тяготения падают с одинаковым ускорением. Следовательно, в данном месте Земли ускорение свободного падения одинаково для всех тел. Оно изменяется вблизи поверхности Земли с широтой в пределах от 9,780 м/с2 на экваторе до 9,832 м/с2 на полюсах. g = 9,81 м/с^2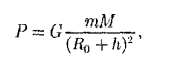

Сила тяжести если тело на высоте h от земли.
Весом тела называют силу, с которой тело действует на опору (или подвес) вследствие гравитационного притяжения к Земле

Вес тела проявляется только в том случае, если тело движется с ускорением, отличным от д, т. е. когда на тело кроме силы тяжести действуют другие силы. Состояние тела, при котором оно движется только под действием силы тяжести, называется состоянием невесомости

Таким образом, сила тяжести действует всегда, а вес проявляется только в том случае, когда на тело кроме силы тяжести действуют еще другие силы
7. Силы упругости. Закон Гука.

Деформация называется упругой, если после прекращения действия внешних сил тело принимает первоначальные размеры и форму. Деформации, которые сохраняются в теле после прекращения действия внешних сил, называются пластическими (или остаточными).

При деформации тела возникают силы упругости. Физическая величина, определяемая модулем силы упругости, действующей на единицу площади поперечного сечения тела, называется напряжением

Если сила направлена по нормали к поверхности, напряжение называется нормальным если же по касательной к поверхности — тангенциальным. Количественной мерой, характеризующей степень деформации, испытываемой телом, является его относительная деформация

Английский физик Р.Гук (1635 — 1703) экспериментально установил, что для малых деформаций относительное удлинение е и напряжение, а пропорциональны друг другу: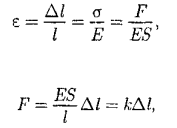

Е – коэффициент пропорциональности, модуль Юнга

Закон Гука согласно которому удлинение стержня при упругой деформации пропорционально действующей на стержень силе

к – коэффициент упругости

8. Силы трения.

Трение бывает:

1) внешнее(сухое)- приходит между двумя телами.

2) внутреннее (жидкое или вязкое)- происходит внутри тела, между слоями.

Если два тела соприкасаются и никуда не движутся- это есть трение покоя, если же движение относительно друг друга при соприкосновении, то различают трение скольжения, качения и верчения.

Внешние трение обусловлено шероховатыми поверхностями. Если поверхности очень гладкие- это есть межмолекулярные силы притяжения.

Условия при которых будет происходить трение(закон): сила трения скольжения пропорциональна силе нормального давления с которым одно тело действует на другое. Тоесть, одно тело должно с большей силой действовать на другое что бы преодолеть силу трения .

Закон трения скольжения для очень гладких поверхностей (р-добавочное давление со стороны межмолекулярного притяжения; Fист- истенный коэфю трения скольжения).

Сила трения качения равна коэфф качения умноженный на нормальное давление делёный на радиус катящегося тела.

9. НИСО. Силы инерции.

Неинерциальной системой отсчета (НИСО) называется система, движущаяся ускоренно относительно инерциальной (ИСО).

Если тело находится в неинерциальной системе отсчета, то законы Ньютона не выполняются. Однако введение сил особого рода - сил инерции, дает возможность использовать второй закон Ньютона и в неинерциальных системах отсчета.

Всякая сила инерции противоположна по направлению ускорению рассматриваемой НИСО относительно выбранной ИСО.



Силу инерции, возникающую во вращающейся системе отсчета, называют центробежной силой инерции.



Кроме центробежных сил инерции, для тела, движущегося относительно вращающейся НИСО с отличной от нуля скоростью в направлении, не совпадающем с мгновенной осью вращения, возникает дополнительная сила инерции – сила Кориолиса.



О на зависит как от свойств НИСО – угловая скорость вращения , так и от скорости частицы относительно этой НИСО - . Вектор силы Кориолиса лежит на прямой, перпендикулярной плоскости векторов.

10. Момент инерции. Момент инерции тела — мера инертности твердых тел при вращательном движении. Моментом инерции системы(тела) относительно данной оси называется физическая величина равная сумме произведений масс n материальных точке системы на квадраты их расстояний до рассматриемовой оси В случае непрерывного распределения масс эта сумма сводится к интегралу .я теоремой Штейнера: момент инерции тела J относительно произвольной оси равен моменту его инерции «/с относительно параллельной оси, проходящей через центр масс С тела, сложенному с произведением массы ттела на квадрат расстояния а между осями:

11. момент силы. Моментом силы относительно неподвижной точки О называется физическая величина М, определяемая векторным произведением радиуса-вектора г, проведенного из точки О в точку Л приложения силы, на силу F(pnc. 27): Моментом силы относительно неподвижной оси z называется скалярпая величина М,, равная проекции на эту ось вектора Л/момента силы, определенного относительно произвольной точки О данной оси z (рис. 28). Значение момента М, не зависит от выбора положения точки О на оси z. Если ось z совпадает с направлением вектора М, то момент силы представляется в виде вектора, совпадающего с осью:

- момент силы относительно оси z.

12.Основное уравнение динамики вращательного движения. уравнение динамики вращательного движения твердого тела относительно неподвижной оси: .

13.Момент импульса. Моментом импульса (количества движения) материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением:

г 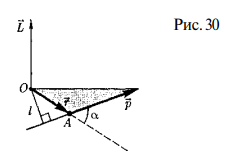де г — радиус-вектор, проведенный из точки О в точку А; р = mv — импульс материальной точки (рис. 30); L — псевдовектор (см. § 4), его направление совпадает с направлением поступательного движения правого винта при его вращении от r к p. Моментом импульса относительно неподвижной оси z называется скалярная величина Ьг , равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси. Момент импульса Lz не зависит от положения точки О на оси z. Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц: еще одна форма уравнения динамики вращательного движения твердого тела относительно неподвижной оси. L=const- закон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т.е. не изменяется с течением времени(фундаментальный закон природы).

1 4. Закон сохранения импульса. Если два или несколько тел взаимодействуют только между собой (то есть не подвергаются воздействию внешних сил), то эти тела образуют замкнутую систему.Импульс, равный векторной сумме импульсов тел, входящих в замкнутую систему, называется суммарным импульсом этой системы.Векторная сумма импульсов тел в замкнутой системе постоянна:p1 + p2 + … + pn = const, где p = mv Суммарный импульс системы тел до взаимодействия равен суммарному импульсу этой системы тел после взаимодействия.

1 5 механическиа энергия, работа, мощность. Энергия — универсальная мера различных форм движения и взаимодействия. Элементарной работой силы F на перемещении dr называется скалярная величина в Джоулях. Чтобы охарактеризовать скорость совершения работы, вводят понятие мощности: в ваттах.

16.Кинетическая энергия. Кинетическая энергия механической системы — энергия механического движения этой системы. Сила F, действуя на покоящееся тело и вызывая его движение, совершает работу, а энергия движущегося тела возрастает на величину затраченной работы.

17. Потенц.сила. Такие поля называются потенциальными, а силы, действующие в них, — консервативными. Если же работа, совершаемая силой, зависит от траектории перемещения тела из одной точки в другую, то такая сила называется диссипативной; ее примером является сила трения. Тела, находясь в потенциальном поле сил, обладают потенциальной энергией П. Потенциальная энергия — механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними.

18. закон сохранения полн. Мех.э. закон сохранения механической энергии: в системе тел, между которыми действуют только консервативные силы, полная механическая энергия сохраняется, т. е. не изменяется со временем Механические системы, на тела которых действуют только консервативные силы (внутренние и внешние), называются консервативными системами. Закон сохранения механической энергии: в консервативных системах полная механическая энергия сохраняется.

19. термодинам. Параметр. Термодинамика — раздел физики, в котором изучаются общие свойства макроскопических систем, находящихся в состоянии термодинамического равновесия, и процессы перехода между этими состояниями. Термодинамика имеет дело с термодинамической системой — совокупностью макроскопических тел, которые взаимодействуют и обмениваются энергией как между собой, так и с другими телами. Основа термодинамического метода — определение состояния термодинамической системы. Состояние системы задается термодинамическими параметрами— совокупностью физических величин, характеризующих свойства термодинамической системы. Обычно в качестве параметров состояния выбирают температуру, давление и удельный объем. Температура — физическая величина, характеризующая состояние термодинамического равновесия макроскопической системы. Термодинамическая температурная шкала определяется по одной реперной точке, в качестве которой взята тройная точка воды.

20. Законы идеального газа. состояние некоторой массы газа определяется тремя термодинамическими параметрами: давлением р, объемом V и температурой Т. Между этими параметрами существует определенная связь, называемая уравнением состояния, которое в общем виде задается выражением уравнееие идеального газа кейплерона-менделеева. Rмолярная газовая постоянная. - для определённой массы где v количества вещества. с постоянной Больцмана.

21.МКТ. или с кейплерона-менделеева. Уравнение, положенное в основу молекулярно-кинетической теории, связывает макроскопические величины, описывающие состояние идеального газа (например, давление) с параметрами его молекул (их массами и скоростями. Основное уравнение МКТ наглядно объясняет, каким образом идеальный газ создает давление на окружающие его стенки сосуда. Молекулы все время ударяются о стенку, воздействуя на нее с некоторой силой F. Тут следует вспомнить третий закон Ньютона: когда молекула ударяется о предмет, на нее действует сила -F, вследствие чего молекула «отбивается» от стенки. При этом мы считаем соударения молекул со стенкой абсолютно упругими: механическая энергия молекул и стенки полностью сохраняется, не переходя во внутреннюю энергию тел. Это значит, что при соударениях изменяются только скорости молекул, а нагревания молекул и стенки не происходит.

22. уравнееие идеального газа кейплерона-менделеева. Rмоля R = 8,31 Дж К∗моль - универсальная газовая постоянная, 𝑅= 𝑁𝑎∗𝑘. k = 1,38 * 10^-23 Дж * К – постоянная Больцмана

23.Распределение Максвелла. Скорости молекул газа имеют различные значения и направления, причем из-за огромного числа соударений, которые ежесекундно испытывает молекула, скорость ее постоянно изменяется. Поэтому нельзя определить число молекул, которые обладают точно заданной скоростью v в данный момент времени, но можно подсчитать число молекул, скорости которых имеют значение, лежащие между некоторыми скоростями v1 и v2 . На основании теории вероятности Максвелл установил закономерность, по которой можно определить число молекул газа, скорости которых при данной температуре заключены в некотором интервале скоростей. Согласно распределению Максвелла, вероятное число молекул в единице объема; компоненты скоростей которых лежат в определённом интервале.

24. Распределение Больцмана. бараметрическая формула. Она позволяет найти атмосферное давление в зависимости от высоты и наоборот. распределение больцмана. Из него следует, что при постоянной температуре плотность газа больше там, где меньше потенциальная энергия его молекул.

25. Работа идеального газа. Количество теплоты. . при изометрическом процессе не меняетсяdQ=dA.

26. Внутренняя энергия идеального газа. внутренняя энергия U — энергия хаотического (теплового) движения микрочастиц системы (молекул, атомов, электронов, ядер и т. д.) и энергия взаимодействия этих частиц .

27. первое начало тернадинамики. соответствии с законом сохранения энергии при любом способе перехода системы из первого состояния во второе изменение внутренней энергии AU= U2— U{ будет одинаковым и равным разности между количеством теплоты Q, полученным системой, и работой А, совершенной системой против внешних сил:

28. Теплоемкость идеального газа. Удельная теплоемкость вещества — величина, равная количеству теплоты, необходимому для нагревания 1 кг вещества на 1 К: с = mdT джоуль. уравнение майнера. оно показывает, что Ср всегда больше Cv на величину молярной газовой постоянной. Это объясняется тем, что при нагревании газа при постоянном давлении требуется еще дополнительное количество теплоты на совершение работы расширения газа, так как постоянство давления обеспечивается увеличением объема газа.

29. Адиабатический процесс. Адиабатным называется процесс, при котором отсутствует теплообмен между системой и окружающей средой (б Q = 0). К адиабатным процессам можно отнести все быстропротекающие процессы. Адиабатным процессом, например, можно считать процесс распространения звука в среде, так как скорость распространения звуковой волны настолько велика, что обмен энергией между волной и средой произойти не успевает. Адиабатные процессы применяются в двигателях внутреннего сгорания (расширение и сжатие горючей смеси в цилиндрах), в холодильных установках и т.д (^v)уравнение пауссона(v-показатель аддиобаты). Процесс при котором теплоёмкость остаётся постоянной явялется политропным.

3 0.циклы. кпд тепловой м. Обратимые процессы — это идеализация реальных процессов. Круговым процессом (или циклом) называется процесс, при котором система, пройдя через ряд состояний, возвращается в исходное. Прямой цикл используется в тепловых двигателях — периодически действующих двигателях, совершающих работу за счет полученной извне теплоты. Обратный цикл используется в холодильных машинах — периодически действующих установках, в которых за счет работы внешних сил теплота переносится к телу с более высокой температурой

31. Цикл Карно. Теорема карно. Из всех периодически действующих тепловых машин, имеющих одинаковые температуры нагревателей (Т1) и холодильников ( Т2 ), наибольшим КПД обладают обратимые машины; при этом КПД обратимых машин, работающих при одинаковых температурах нагревателей (Т1 ) и холодильников (Т2 ), равны друг другу и не зависят от природы рабочего тела (тела, совершающего круговой процесс и обменивающегося энергией с другими телами), а определяются только температурами нагревателя и холодильника. .(t1=t2) при изохор. (v1=v2) Энтропия обладает свойством аддитивности: энтропия системы равна сумме энтропий тел, входящих в систему. 33 Второе и третье начало термодинамики

Второе:

1) по Кельвину: невозможен круговой прогресс, единственным результатом которого является превращение теплоты, полученной от нагревателя, в эквивалентную ей работу;

2) по Клаузиусу: невозможен круговой процесс, единственным результатом которого является передача теплоты от менее нагретого тела к более нагретому

Третье:

теоремой Нернстах — Планка: энтропия всех тел в состоянии равновесия стремится к нулю по мере приближения температуры к нулю кельвин:



34 Свойство электрического заряда. Закон кулона

заряды, подобные возникающим на стекле, потертом о кожу (их назвали положительными), и заряды, подобные возникающим на эбоните, потертом о мех (их назвали отрицательными); одноименные заряды друг от друга отталкиваются, разноименные — притягиваются.

Заряд дискретен, т.е. заряд любого тела составляет целое кратное от элементарного электрического заряда е

Всякий процесс заряжения сводится к разделению зарядов, при котором на одном из тел (или части тела) появляется избыток положительного заряда, а на другом (или другой части тела) — избыток отрицательного заряда. Общее количество зарядов обоих знаков, содержащихся в телах, не изменяется: эти заряды только перераспределяются между телами

Закон кулона: сила взаимодействия F между двумя неподвижными точечными зарядами, находящимися в вакууме, пропорциональна зарядам Ql и Q2 и обратно пропорциональна квадрату расстояния г между ними:



к — коэффициент пропорциональности, зависящий от выбора системы единиц

Сила F направлена по прямой, соединяющей взаимодействующие заряды, т.е. является центральной, и соответствует притяжению (F < 0) в случае разноименных зарядов и отталкиванию (F> 0) в случае одноименных. Эта сила называется кулоновской силой. В векторной форме закон Кулона имеет вид





где F12 — сила, действующая на заряд Qx со стороны заряда Q2 ', r 12 — радиусвектор, соединяющий заряд Q2 с зарядом Q1i, r= |r12| (рис. 119). На заряд Q2 со стороны заряда Q1 действует сила F21 = -F12 .

35 Напряженность электростатического поля. Силовые линии

Напряженность электростатического поля в данной точке есть физическая величина, определяемая силой, действующей на пробный единичный положительный заряд, помещенный в эту точку поля:



напряженность поля точечного заряда в вакууме

Направление вектора Е совпадает с направлением силы, действующей на положительный заряд. Если поле создается положительным зарядом, то вектор Ё направлен вдоль радиуса-вектора от заряда во внешнее пространство (отталкивание пробного положительного заряда); если поле создается отрицательным зарядом, то вектор Ё направлен к заряду (рис. 120).



единица напряженности электростатического поля — ньютон на кулон (Н/Кл):

36

Поток напряженности электростатического поля. Теорема Гаусса

Величина называется потоком вектора напряженности сквозь площадку dS. Здесь &S = dSn — вектор, модуль которого равен dS, а направление совпадает с направлением нормали п к площадке. Выбор направления вектора п (а следовательно, и dS) условен, так как его можно направить в любую сторону. Единица потока вектора напряженности электростатического поля — вольтметр (В • м). Для произвольной замкнутой поверхности S поток вектора Е сквозь эту поверхность



де интеграл берется по замкнутой поверхности S. Поток вектора Е является алгебраической величиной: зависит не только от конфигурации поля Ё, но и от выбора направления п. Для замкнутых поверхностей за положительное направление нормали принимается внешняя нормаль, т.е. нормаль, направленная наружу области, охватываемой поверхностью

Гаусса

выражает теорему Гаусса для электростатического поля в вакууме: поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной па е0 .



37 Применение теоремы гаусса к расчёту полей различных источников

Поле равномерно заряженной бесконечной плоскости.



Поле двух бесконечных параллельных разноименно заряженных плоскостей



Поле равномерно заряженной сферической поверхности



Поле объемно заряженного шара.



Поле равномерно заряженного бесконечного цилиндра (нити)



38 Работа сил электростатического поля. Потенциал

Работа, совершаемая силами электростатического поля при перемещении заряда Q0 ИЗ ТОЧКИ 1 в точку 2



т. е. равна произведению перемещаемого заряда на разность потенциалов в начальной и конечной точках

Потенциал ф в какой-либо точке электростатического поля есть физическая величина, определяемая потенциальной энергией единичного положительного заряда, помещенного в эту точку



потенциал поля, создаваемого точечным зарядом Q, равен



39 Проводники в электростатическом поле.Электроемкость проводника

Если поместить проводник во внешнее электростатическое поле или его зарядить, то на заряды проводника будет действовать электростатическое поле, в результате чего они начнут перемещаться. Перемещение зарядов (ток) продолжается до тех пор, пока не установится равновесное распределение зарядов, при котором электростатическое поле внутри проводника обращается в нуль.

Емкость уединенного проводника определяется зарядом, сообщение которого проводнику изменяет его потенциал на единицу.



Емкость проводника зависит от его размеров и формы, но не зависит от материала, агрегатного состояния, формы и размеров полостей внутри проводника. Это связано с тем, что избыточные заряды распределяются на внешней поверхности проводника. Емкость также не зависит от заряда проводника и его потенциала. Единица электроемкости — фарад

40 Конденсаторы

устройства, обладающие способностью при малых размерах и небольших относительно окружающих тел потенциалах накапливать значительные по величине заряды, иными словами, обладать большой емкостью. Эти устройства получили название конденсаторов.

Конденсатор состоит на двух проводников (обкладок), разделенных диэлектриком.

емкости плоского конденсатора:



41 Связь напряженности и потенциала

вектор напряженности Е поля направлен в сторону убывания потенциала

42 Полярные и неполярные молекулы. Поляризация диэлектриков

положительный заряд всех ядер молекулы равен суммарному заряду электронов, то молекула в целом электрически нейтральна. Если заменить положительные заряды ядер молекул суммарным зарядом + Q, находящимся в центре «тяжести» положительных зарядов, а заряд всех электронов — суммарным отрицательным зарядом - Q, находящимся в центре «тяжести» отрицательных зарядов, то молекулу можно рассматривать как электрический диполь с электрическим моментом,

Первую группу диэлектриков (N2 , Н2 , О2 , СО2 , СН4 , ...) составляют вещества, молекулы которых имеют симметричное строение, т. е. центры «тяжести» положительных и отрицательных зарядов в отсутствие внешнего электрического поля совпадают и, следовательно, дипольный момент р молекулы равен нулю. Молекулы таких диэлектриков называются неполярными.

Вторую группу диэлектриков (Н2О, NH3 , SO2 , CO,...) составляют вещества, молекулы которых имеют асимметричное строение, т.е. центры «тяжести» положительных и отрицательных зарядов не совпадают. Таким образом, эти молекулы в отсутствие внешнего электрического поля обладают динольным моментом. Молекулы таких диэлектриков называются полярными.

Поляризацией диэлектрика называется процесс ориентации диполей или появления под воздействием внешнего электрического поля ориентированных по полю диполей. Соответственно трем группам диэлектриков различают три вида поляризации: электронная, или деформационная, поляризация диэлектрика с неполярными молекулами, заключающаяся в возникновении у атомов индуцированного диполыюго момента за счет деформации электронных орбит; ориентационная, или дипольная, поляризация диэлектрика с полярными молекулами, заключающаяся в ориентации имеющихся дипольных моментов молекул по полю.

ионная поляризация диэлектриков с ионными кристаллическими решетками, заключающаяся в смещении подрешетки положительных ионов вдоль поля, а отрицательных — против поля, приводящем к возникновению дипольных моментов.

43 Вектор электрической индукции

Векторная величина, обозначаемая D


где ε 0 - электрическая постоянная, → E - вектор напряженности, → P - вектор поляризации.

44 Электрический ток. Сила тока. Плотность тока

Электрическим током называется любое упорядоченное (направленное) движение электрических зарядов. В проводнике под действием приложенного электрического поля Ё свободные электрические заряды перемещаются: положительные — по полю, отрицательные — против поля т.е. в проводнике возникает электрический ток, называемый током проводимости.

сила тока I — скалярная физическая величина, определяемая электрическим зарядом, проходящим через поперечное сечение проводника в единицу времени:



Если сила тока и его направление не изменяются со временем, то такой ток называется постоянным. Для постоянного тока где Q — электрический заряд, проходящий за время t через поперечное сечение проводника. Единица силы тока — ампер

Физическая величина, определяемая силой тока, проходящего через единицу площади поперечного сечения проводника, перпендикулярного направлению тока, называется плотностью тока:



Плотность тока — вектор; направление вектора j совпадает с направлением упорядоченного движения положительных зарядов



Единица плотности тока — ампер на метр в квадрате

45

ЭДС. Разность потенциалов. Напряжение

Сторонние силы совершают работу по перемещению электрических зарядов. Физическая величина, определяемая работой, совершаемой сторонними силами при перемещении единичного положительного заряда, называется электродвижущей силой (ЭДС),



ЭДС, действующей в цепи:



Разность потенциалов двух точек 1 в 2 в электростатическом поле определяется работой, совершаемой силами поля, при перемещении единичного положительного заряда из точки 1 в точку 2. При решении конкретных задач физический смысл имеет разность потенциалов между двумя точками электростатического поля



Напряжением U на участке 1 — 2 называется физическая величина, определяемая работой, совершаемой суммарным полем электростатических (кулоновских) и сторонних сил при перемещении единичного положительного заряда на данном участке цепи.



46 Закон ома для постоянного тока. Сопротивление проводников



Сопротивление проводников зависит от его размеров и формы, а также от материала, из которого проводник изготовлен. Для однородного линейного проводника сопротивление R прямо пропорционально его длине I и обратно пропорционально площади его поперечного сечения S:



где р — коэффициент пропорциональности, характеризующий материал проводника и называемый удельным электрическим сопротивлением. Единица удельного электрического сопротивления — ом-метр

47 Закон Джоуля ленца. Мощность и работа тока



Количество теплоты, выделяющееся за единицу времени в единице объема, называется удельной тепловой мощностью тока. Она равна



Работа тока



Мощность тока



48

49 Правило кирхгофа

Первое правило Кирхгофа: алгебраическая сумма токов, сходящихся в узле, равна нулю:



второе правило Кирхгофа: в любом замкнутом контуре, произвольно выбранном в разветвленной электрической цепи, алгебраическая сумма произведений сил токов /г на сопротивления R{ соответствующих участков этого контура равна алгебраической сумме ЭДС &к , встречающихся в этом контуре:



50 Газовый разряд. Электролиз

Прохождение электрического тока через газы называется газовым разрядом.

В зависимости от давления газа, конфигурации электродов, параметров внешней цепи можно говорить о четырех типах самостоятельного разряда: тлеющем, искровом, дуговом и коронном.

Электролиз - комплекс окислительно восстановительных реакций, которые протекают в жидкости под действием тока.



51 Магнитное поле. Вектор магнитной индукции

в пространстве, окружающем токи и постоянные магниты, возникает силовое поле, называемое магнитным. Магнитная индукция в данной точке однородного магнитного поля определяется максимальным вращающим моментом, действующим на рамку с магнитным моментом, равным единице, когда нормаль к рамке перпендикулярна направлению поля.



Так как магнитное поле является силовым, то его, по аналогии с электрическим, изображают с помощью линий магнитной индукции — линий, касательные к которым в каждой точке совпадают с направлением вектора В. Их направление задается правилом правого винта: головка винта, ввинчиваемого по направлению тока, вращается в направлении линий магнитной индукции.

52 Закон Био-Савара-Лапласа



где dl — вектор, по модулю равный длине dl элемента проводника и совпадающий по направлению с током; г — радиус-вектор, проведенный из элемента dl проводника в точку Л поля; г — модуль радиуса-вектора г.

53 Вычисление полей с помощью закона БСЛ для прямого и кольцевого тока

Магнитное поле прямого тока



Магнитное поле в центре кругового проводника с током



54 теорема о циркуляции для вектора магнитной индукции

циркуляция вектора магнитной индукции равна току, охваченному контуром, умноженному на магнитную постоянную.



55 Вычесление полей соленоида и торонда с помощью теоремы о циркуляции

Магнитное поле соленоида



Магнитное поле тороида



56 Магнитное поле в веществе. Намагниченность. Магнитная восприимчивость

все вещества, помещенные в магнитное поле, намагничиваются. Электрон, движущийся по одной из таких орбит, эквивалентен круговому току, поэтому он обладает орбитальным магнитным моментом

количественного описания намагничивания магнетиков вводят векторную величину — намагниченность, определяемую магнитным моментом единицы объема магнетика:



Следовательно, магнитное поле в веществе складывается из двух полей: внешнего поля, создаваемого током, и поля, создаваемого намагниченным веществом.

Как показывает опыт, в носильных полях намагниченность пропорциональна напряженности поля, вызывающего намагничивание, т.е



где х — безразмерная величина, называемая магнитной восприимчивостью вещества

57 Напряженность магнитного поля. Магнитная проницаемость



Напряженность не зависит от среды.

Магнитная проницаемость вещества – скалярная физическая величина, характеризующая связь между магнитной индукции В и напряженностью магнитного поля в веществе

58 Сила Ампера

Одним из проявлений магнитного поля является его силовое воздействие на проводник с током. Ампер установил, что на проводник с током, помещенный в однородное магнитное поле с индукцией В действует сила, пропорциональная силе тока и магнитной индукции:

Закон Ампера для прямолинейного проводника в однородном магнитном поле:



Закон Ампера для проводника произвольной формы в неоднородном магнитном поле:



Idl - элемент тока, малый участок проводника, имеющий направление, совпадающее с направлением тока в проводнике.

Направление силы Ампера определяется по правилу левой руки: если 4 пальца левой руки расположить по направлению тока в проводнике, а индукция магнитного поля входит в ладонь, то отогнутый большой палец укажет направление силы Ампера

59 Действие магнитного поля на рамку с током

Действие магнитного поля на проводник с током проявляется не только в притяжении или отталкивании.

Рассмотрим проволочную проводящую рамку, находящуюся во внешнем магнитном поле. Если в этой рамке создать электрический ток, то на рамку со стороны магнитного поля начнут действовать силы Ампера.

Если внешнее магнитное поле является однородным, то равнодействующая всех сил Ампера будет равна нулю, однако момент всех сил Ампера в нуль обращаться не будет, что означает то, что рамка начнет вращаться (создается вращающий момент, и рамка поворачивается в положение, в котором вектор магнитной индукции перпендикулярен плоскости рамки).

На данном факте основано действие электродвигателя постоянного тока (электромотора).

Если внешнее магнитное поле является неоднородным, то равнодействующая всех сил Ампера и момент всех сил не будут равны нулю, то есть свободная рамка начнет поступательно двигаться плюс вращаться (неоднородное магнитное поле ориентирует, а также притягивает или отталкивает рамку с током).

Опыт: подвесим около длинного тонкого вертикально расположенного проводника на тонких и гибких подводящих проводах маленькую (по сравнению с расстоянием, на котором магнитное поле заметно изменяется, т. е. подальше от проводника) рамку. При пропускании по проводнику и рамке электрического тока рамка поворачивается и располагается так, что оказывается в одной плоскости с проводником с током. Таким образом, магнитное поле оказывает на рамку с током ориентирующее действие, аналогичное действию на стрелку компаса.

60 Сила Лоренца

Сила Лоренца - действует на движущийся заряд со стороны магнитного поля. Так как электрический ток представляет собой упорядоченное движение зарядов, то действие магнитного поля на проводник с током есть результат его действия на отдельные движущиеся заряды.Силу, действующую со стороны магнитного поля на движущиеся в нем заряды, называют силой Лоренца.



q - величина движущегося заряда; V - модуль его скорости;

B - модуль вектора индукции магнитного поля;

a - угол между вектором скорости заряда и вектором магнитной индукции.

61 Движение заряженной частицы в магнитном поле

ли скорость V заряженной частицы массой m направлена вдоль вектора индукции магнитного поля, то частица будет двигаться по прямой с постоянной скоростью (сила Лоренца = 0, так как a= 0)

Если скорость V заряженной частицы массой m перпендикулярна вектору индукции магнитного поля, то частица будет двигаться по радиусу R окружности, плоскость которой перпендикулярна линиям индукции. Тогда второй закон Ньютона можно записать в следующем виде:

Fл=m*a,

так как скорость частицы перпендикулярна вектору магнитной индукции.

Тогда:

62 Поток вектора магнитной индукции. Теорема гаусса для B,H,J

Потоком вектора магнитной индукции В (магнитным потоком) через малую поверхность площадью dS называется скалярная физическая величина, равная



Теорема Гаусса для поля В: поток вектора магнитной индукции сквозь любую замкнутую поверхность равен нулю



Теорема Гаусса для H



Теорема Гаусса для J



63 Работа по перемещению проводника с током

Работа, совершаемая проводником с током при перемещении, численно равна произведению тока на магнитный поток, пересечённый этим проводником:



64 Опыт Фарадея. Основной закон электромагнитной индукции.

Опыт Фарадея. Опыт 1. Если в замкнутый на гальванометр соленоид вдвигать или выдвигать постоянный магнит, то в моменты его вдвигания или выдвигания наблюдается отклонение стрелки гальванометра (возникает индукционный ток); направления отклонений стрелки при вдвигании и выдвигании магнита противоположны. Отклонение стрелки гальванометра тем больше, чем больше скорость движения магнита относительно катушки. При изменении полюсов магнита направление отклонения стрелки изменится. Для получения индукционного тока магнит можно оставлять неподвижным, тогда нужно относительно магнита передвигать соленоид.

Опыт 2. Концы одной из катушек, вставленных одна в другую, присоединяются к гальванометру, а через другую катушку пропускается ток. Отклонение стрелки гальванометра наблюдается в моменты включения или выключения тока, в моменты его увеличения или уменьшения, при перемещении катушек друг относительно друга. Направления отклонений стрелки гальванометра также противоположны при включении или выключении тока, его увеличении или уменьшении, сближении или удалении катушек.

Основной закон электромагнитной индукции.

Для любого контура индуцированная ЭДС равна и противоположна по знаку скорости изменения магнитного потока, проходящего через этот контур.

При этом индукционный ток направлен таким образом, что его действие противоположно действию причины, вызвавшей этот ток (правило Ленца).

65 Вращение рамки с током в магнитном поле

Явление электромагнитной индукции применяется для преобразования механической энергии в энергию электрического тока.

Пусть рамка вращается в однородном магнитном поле (В= const) равномерно с угловой скоростью ω = const. Магнитный поток, сцепленный с рамкой площадью S, в любой момент времени t, равен



где а — ωt — угол поворота рамки в момент времени t . При вращении рамки в ней будет возникать переменная ЭДС индукции

изменяющаяся со временем по гармоническому закону. ЭДС Еi максимальна при sinωt = 1

Таким образом, если в однородном магнитном поле равномерно вращается рамка, то в ней возникает переменная ЭДС, изменяющаяся по гармоническому закону

Процесс превращения механической энергии в электрическую обратим. Если по рамке, помещенной в магнитное поле, пропускать ток, то в соответствии с на нее будет действовать вращающий момент и рамка начнет вращаться.

66 Явление самоиндукци. Индуктивность

Электрический ток, текущий в замкнутом контуре, создает вокруг себя магнитное поле, индукция которого, по закону Био —Савара — Лапласа [см. (110.2)], пропорциональна току. Сцепленный с контуром магнитный поток Ф поэтому пропорционален току в контуре:



где L — коэффициент пропорциональности, называемый индуктивностью контура.

При изменении силы тока в контуре будет изменяться также и сцепленный с ним магнитный поток; следовательно, в контуре будет индуцироваться ЭДС. Возникновение ЭДС индукции в проводящем контуре при изменении в нем силы тока называется самоиндукцией

67 Явление взаимной индукции. Трансформаторы

Явление возникновения ЭДС в одном из контуров при изменении силы

тока в другом называется взаимной индукцией. Таким образом, взаимная индуктивность двух катушек, намотанных па общий тороидальный сердечник,



Ток 1{ первичной обмотки определяется согласно закону Ома:



токи в обмотках обратно пропорциональны числу витков в этих обмотках.

68 Установление и исчезновение тока в цепи

Любая электрическая цепь представляет собой контур, содержащий источник тока, провода, потребители. Поэтому она обладает индуктивностью (отношение потока магнитной индукции к силе тока в этом контуре).

В нем индуктивность цепи показана в виде катушки, включенной в цепь. При замыкании и размыкании цепи в ней возникает ЭДС самоиндукции, которая в соответствии с правилом Ленца направлена против ЭДС источника тока при замыкании и в направлении ЭДС источника тока при разпри замыкании цепи ток в ней возрастает постепенно с постоянной времени τ.При размыкании цепи ток исчезает не сразу, убывает постепенно с постоянной времени τ.мыкании цепи.

69 Энергия магнитного поля

Проводник, по которому протекает электрический ток, создает в окружающем пространстве магнитное поле, причем магнитное поле появляется и исчезает вместе с появлением и исчезновением тока.

Магнитное поле, подобно электрическому, является носителем энергии. Естественно предположить, что энергия магнитного поля равна работе, которая затрачивается током на создание этого поля.

Э нергия магнитного поля, связанного с контуром:

М агнитное поле соленоида однородно и сосредоточено внутри пего, поэтому энергия заключена в объеме соленоида и распределена в нем с постоянной объемной плотностью:

70 Парамагнетизм, диамагнетизм, ферромагнетизм.

Всякое вещество является магнетиком, т.е. оно способно под действием магнитного поля приобретать магнитный момент (намагничиваться).

Электронные орбиты атома под действием внешнего магнитного поля совершают прецессионное движение, которое эквивалентно круговому току. Так как этот микроток индуцирован внешним магнитным полем, то, согласно правилу Ленца, у атома появляется составляющая магнитного поля, направленная противоположно внешнему полю. Наведенные составляющие магнитных полей атомов (молекул) складываются и образуют собственное магнитное поле вещества, ослабляющее внешнее магнитное поле. Этот эффект получил название диамагнитного эффекта, а вещества, намагничивающиеся во внешнем магнитном поле против направления поля, называются диамагнетиками.

Однако наряду с диамагнетиками существуют и парамагнетики — вещества, намагничивающиеся во внешнем магнитном поле по направлению поля. У парамагнитных веществ при отсутствии внешнего магнитного поля магнитные моменты электронов не компенсируют друг друга, и атомы (молекулы) парамагнетиков всегда обладают магнитным моментом. Однако вследствие теплового движения молекул их магнитные моменты ориентированы беспорядочно, поэтому парамагнитные вещества магнитными свойствами не обладают. При внесении парамагнетика во внешнее магнитное поле устанавливается преимущественная ориентация магнитных моментов атомов по полю (полной ориентации препятствует тепловое движение атомов). Таким образом, парамагнетик намагничивается, создавая собственное магнитное иоле, совпадающее по направлению с внешним полем и усиливающее его. Этот эффект называется парамагнитным.

Помимо рассмотренных двух классов веществ — диа- и парамагнетиков, называемых слабомагнитными веществами, существуют еще сильномагнитные вещества — ферромагнетики — вещества, обладающие спонтанной намагниченностью, т.е. они намагничены даже при отсутствии внешнего магнитного поля. К ферромагнетикам кроме основного их представителя — железа (от него и идет название «ферромагнетизм») — относятся, например, кобальт, никель, гадолиний, их сплавы и соединения.

71 Вихревое электрическое поле. Ток смещения

циркуляция вектора Ев в отличие от циркуляции вектора EQ не равна пулю. Следовательно, электрическое поле Ев> возбуждаемое магнитным полем, как и само магнитное поле (см. § 118), является вихревым.

Для установления количественных отношений между изменяющимся электрическим полем и вызываемым им магнитным полем Максвелл ввел в рассмотрение так называемый ток смещения

плотностью тока смещения



7 2 Уравнение максвелла

Из уравнений Максвелла вытекает, что источниками электрического поля могут быть либо электрические заряды, либо изменяющиеся во времени магнитные поля, а магнитные поля могут возбуждаться либо движущимися электрическими зарядами (электрическими токами), либо переменными электрическими полями. Уравнения Максвелла не симметричны относительно электрического и магнитного полей. Это связано с тем, что в природе существуют электрические заряды, по отсутствуют магнитные

Д ля стационарных полей (Е — const и В — const) уравнения Максвелла примут вид

т.е. источниками электрического поля в данном случае являются только электрические заряды, а источниками магнитного — только токи проводимости. В данном случае электрические и магнитные поля независимы друг от друга, что и позволяет изучать отдельно постоянные электрическое и магнитное поля.

73. Свободные электромагнитные колебания. электромагнитные колебания, при которых электрические величины (заряды, токи) периодически изменяются и которые сопровождаются взаимными превращениями электрического и магнитного полей. Для возбуждения и поддержания электромагнитных колебаний используется колебательный контур — цепь, состоящая из включенных последовательно катушки индуктивностью L, 258 конденсатора емкостью С и резистора сопротивлением R. (на нагревание не расходуется. эдс отсутствет.

74. затухающие колебания — колебания, амплитуды которых из-за потерь энергии реальной колебательной системой с течением времени уменьшаются .

76. ома переменный ток. Переменный ток можно считать квазистационарным, т. е. для него мгновенные значения силы тока во всех сечениях цепи практически одинаковы, так как их изменения происходят достаточно медленно, а электромагнитные возмущения распространяются по цепи со скоростью, равной скорости света. Z полное сопротивление.

77 .Заряды, движущиеся с ускорением, распространяют вокруг себя изменение электрического поля, которое порождает изменяющееся вихревое магнитное поле. В свою очередь, изменяющееся магнитное поле порождает вихревое электрическое поле, а это электрическое поле – вновь порождает вихревое магнитное.Такая распространяющаяся в пространстве структура взаимоподдерживающихся вихревых электрического и магнитного полей называется электромагнитной волной. Может поглащать, приломлять, интерфирировать.

78. Импульс электромагнитной волны. Давление света.

Электромагнитные волны оказывают на тела давление: