Практическое задание 3. Ответ 12341 способами
 Скачать 16.38 Kb. Скачать 16.38 Kb.
|
|
Задание №1 1. В домашней библиотеке у Василия Петровича собрано 43 книги по научной фантастике. Он хочет взять с собой в отпуск 3 книги для чтения. Сколькими способами Василий Петрович может это сделать? 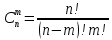 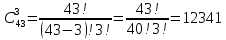 Ответ: 12341 способами. 2. В кино отправились 9 друзей. Сколькими разными способами они могут встать в очередь на кассе? P9 = 9! = 9  8 8 7 7  6 6 5 5  4 4  3 3  2 2  1 = 362880 способами 1 = 362880 способами3. Таблица, размером 99*99, раскрашена в шахматном порядке в белый и черный цвета. Верхняя левая клетка – черная. Сколькими способами можно указать в таблице два квадрата – белый и черный? 99  99 = 9801 (кл.) всего в таблице. Черных клеток в черной таблице на 1 больше, т.к. верхняя белая клетка черная. 99 = 9801 (кл.) всего в таблице. Черных клеток в черной таблице на 1 больше, т.к. верхняя белая клетка черная.(9801 – 1) / 2 = 4900 (кл.) белые 4900 + 1 = 4901 (кл.) черные 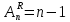 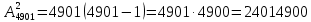 Задание №2 Задание №21. При игре в кости бросаются два игральных кубика и подсчитывается сумма выпавших очков. Найти вероятность событий: А – сумма равна 6; В – сумма больше 8. Число всевозможных подбрасывания кубиков: п = 6  6 = 36. Исходы будем представлять как упорядоченные пары чисел вида (х, у), где число выпадения очков на первой кости, у число выпадения очков на второй кости. Найдём все исходы: сумма выпавших очков равна 6, т. е. 6 + y = 6. 6 = 36. Исходы будем представлять как упорядоченные пары чисел вида (х, у), где число выпадения очков на первой кости, у число выпадения очков на второй кости. Найдём все исходы: сумма выпавших очков равна 6, т. е. 6 + y = 6.(1;5), (2; 4), (3:3), (4; 2), (5; 1). - m = 5 благоприятных исходов. Вероятность события А: P(A) = 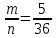 Найдём все исходы: сумма выпавших очков больше 8, т.е. x + y 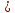 8 8(3;6), (4; 5), (4; 6), (5; 4), (5; 5), (5: 6), (6; 3), (6; 4), (6; 5), (6; 6) - m = 10 благоприятных исходов. Вероятность события В: P(B) = 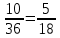 Ответ: P(A) = 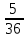 ; Р(В) = ; Р(В) =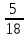 2. Из имеющихся 16 телевизоров 11 готовы к продаже, а 5 требуют дополнительной регулировки. Найти вероятности событий: А – из случайно отобранных 4 телевизоров все хорошие, В – два хорошие и два нет, С – один хороший и три нет, D – хороших нет. А — из случайно отобранных 4 телевизора все хорошие; В — два хорошие и два нет; С — один хороший и три нет; D — хороших нет. Общее число элементарных исходов равно числу способов выбрать 4 телевизоров из 16. Т.е. 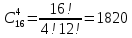 1) Вероятность события А. Число благоприятных исходов: выбрать 4 хороших телевизора из 11 можно 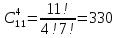 Искомая вероятность: 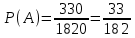 2) Вероятность события В: Число благоприятных исходов: выбрать два хороших телевизора можно 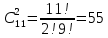 способами, а два НЕ хороших телевизора можно способами, а два НЕ хороших телевизора можно 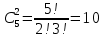 . .По правилу произведения, всего таких способов: 55  10 = 550 10 = 550Искомая вероятность: 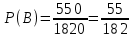 3) Вероятность события C: Выбрать один хороший телевизор можно 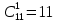 .способами. Выбрать три НЕ хороших телевизора можно .способами. Выбрать три НЕ хороших телевизора можно 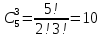 способами. По правилу произведения, таких способов 11 способами. По правилу произведения, таких способов 11  10 = 110 10 = 110Искомая вероятность: 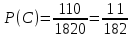 4) Вероятность события D Выбрать четыре НЕ хороших телевизора можно 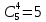 способами. способами.Искомая вероятность: 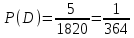 3. Туристическая группа состоит из 10 юношей и 6 девушек. По жребию (случайным образом) выбирают 3 дежурных. Найти вероятность того, что будут выбраны 1 девушка и 2 юноши. Всего 10+6=16 человек. Находим вероятность 1 девушки: 1 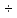 16 = 0,0625 - это и есть вероятность, что будет выбрана одна девушка. 16 = 0,0625 - это и есть вероятность, что будет выбрана одна девушка.Находим вероятность 2 юношей: 2 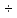 16 = 0,125 - вероятность, что будет выбрано 2 юноши. 16 = 0,125 - вероятность, что будет выбрано 2 юноши. |
