Ответы на матанализ. Ответы на экзамен по матанализу Первообразная функции. Свойства функций, имеющих первообразную
 Скачать 4.64 Mb.
|
|
Ответы на экзамен по матанализу Первообразная функции. Свойства функций, имеющих первообразную.  Неопределенный интеграл и его свойства.    Непосредственное интегрирование.  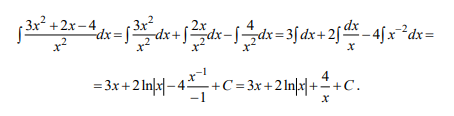 Таблица неопределенных интегралов.  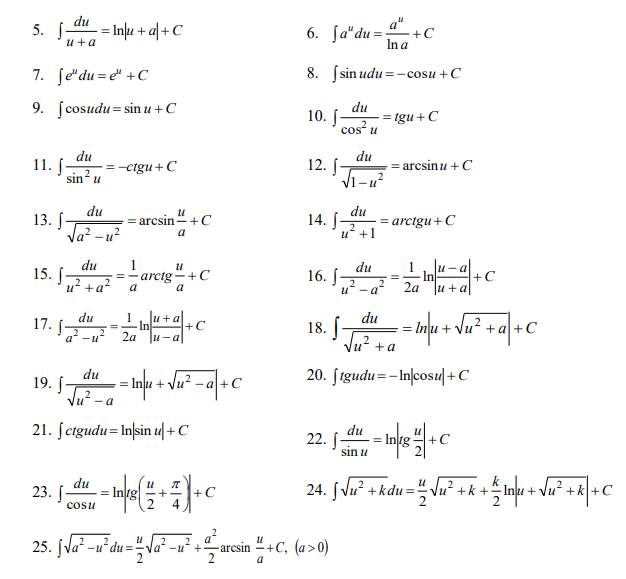 Интегрирование по частям.     Замена переменной (интегрирование подстановкой).  Иногда требуется взять формулу  тогда Интегрирование простейших рациональных дробей. 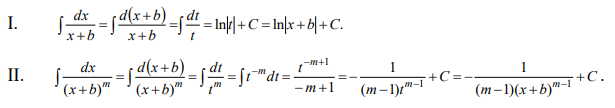 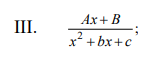 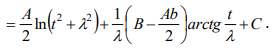  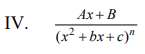 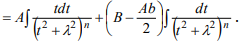 Рекуррентная функция 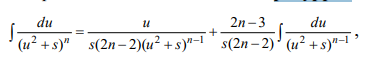 Интегрирование рациональных функций.      Интегрирование дробно-линейных иррациональностей. 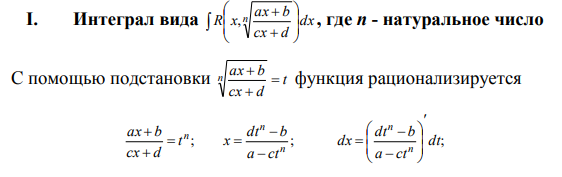 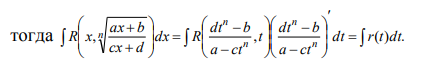 Интегрирование квадратных иррациональностей (первая подстановка Эйлера).   Интегрирование квадратных иррациональностей (вторая подстановка Эйлера).   Интегрирование функций вида 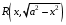 ;  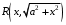;  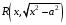.  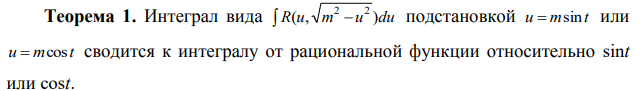т 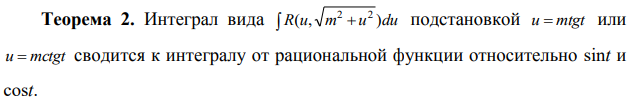 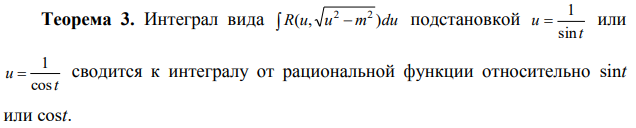 Интегрирование биномиальных дифференциалов. 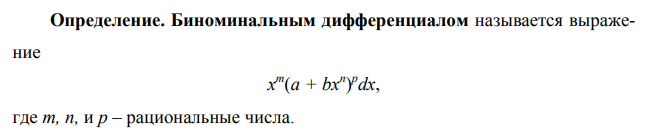  Интегрирование тригонометрических функций вида 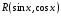 (универсальная подстановка). Интегрирование тригонометрических функций вида 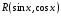(частные случаи).1)  Рационально применить подстановку t = sin(x)  2)  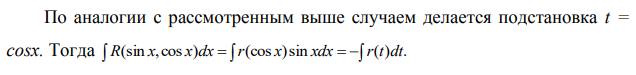 3) 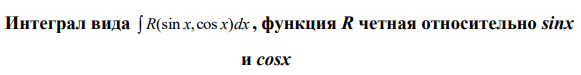 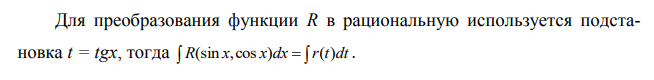 Интегралы вида 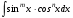 . Интегрирование тригонометрических функций (универсальная подстановка, произведение синусов и косинусов). 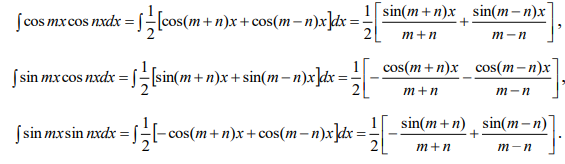 Определенный интеграл Римана.??  Задачи, приводящие к понятию определенного интеграла. Определенный интеграл, необходимое условие его существования. 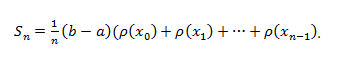 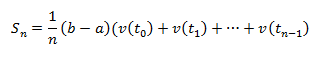      Непрерывность функции является достаточным условием ее интегрируемости Площадь фигуры в декартовых координатах?? 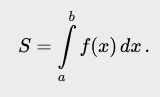 Площадь криволинейной трапеции. Определение определенного интеграла. ??  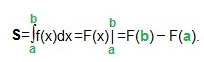  Определение определенного интеграла. Необходимое условие интегрируемости функции.  Свойства определенного интеграла.  Теорема о среднем. 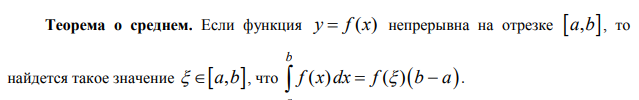  Свойства определенного интеграла, выраженные неравенствами. 1 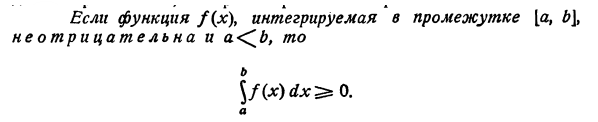 2 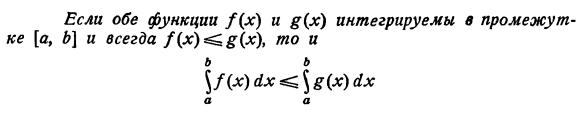 3 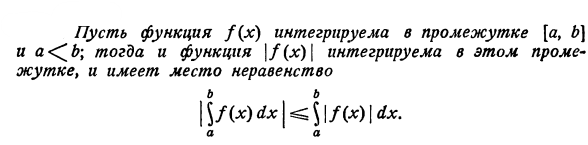 4  Определенный интеграл как функция верхнего предела. 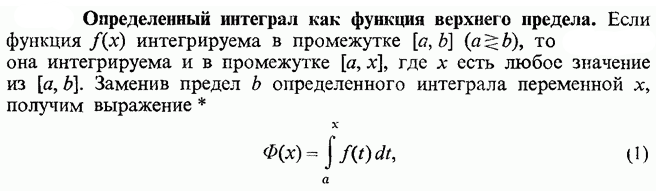 Вычисление определенного интеграла. Формула Ньютона-Лейбница. Вычисление опр. Интеграла см. 29, 30  Интегрирование по частям в определенном интеграле. 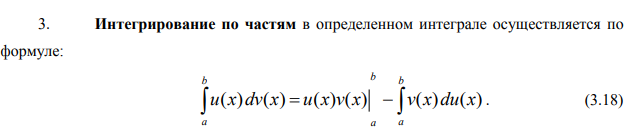 Замена переменной в определенном интеграле.  Площадь фигуры в декартовых координатах. 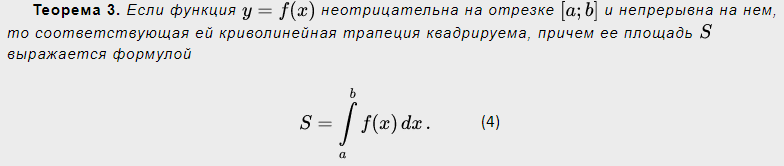 Площадь фигуры для случая параметрического задания кривой. 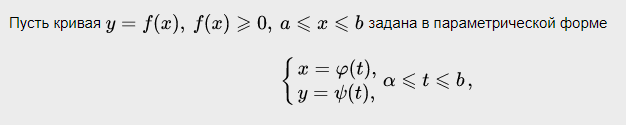 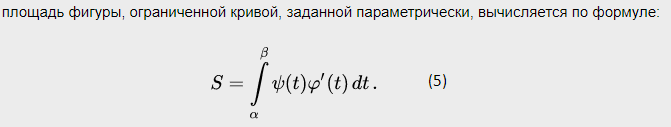   Площадь сектора в полярных координатах. 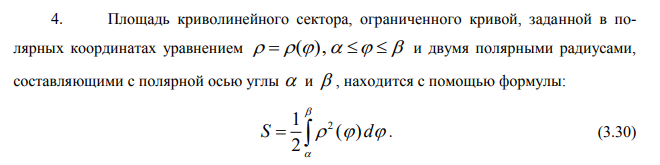 Длина дуги кривой для случая, когда кривая задана уравнением y=f(x) 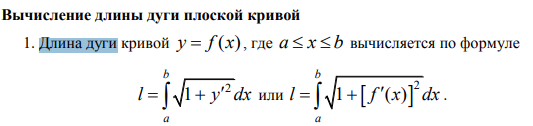 Длина дуги кривой в полярных координатах. 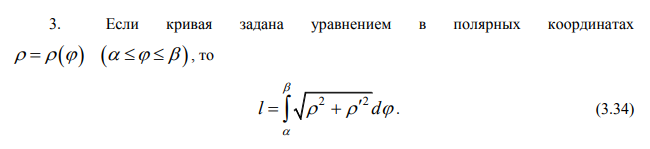 Длина дуги кривой, заданной в параметрическом виде. 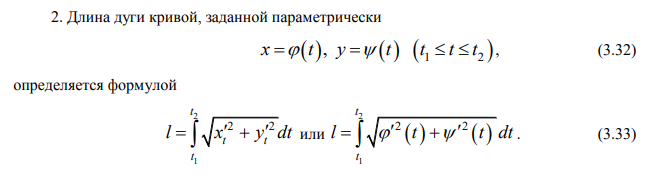 Дифференциал дуги.  Площадь поверхности вращения в прямоугольных координатах.  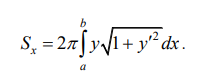 Площадь поверхности вращения, когда кривая задана параметрическими уравнениями.  Площадь поверхности вращения, когда кривая задана в полярной системе координат. 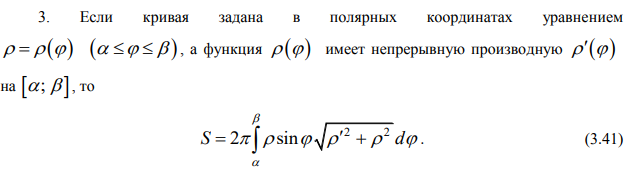 Объем тела вращения.  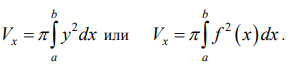 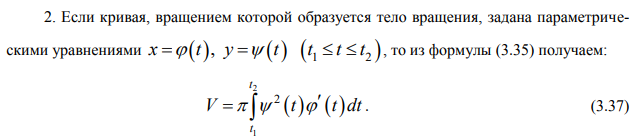 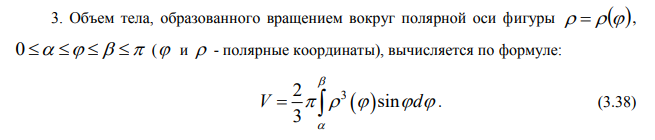 Несобственные интегралы I – го рода.  Н  есобственные интегралы первого рода, признаки их сходимости.    Свойства несобственных интегралов I – го рода.  Первое и второе достаточные условия сходимости и расходимости несобственных интегралов I – го рода. Несобственные интегралы II – го рода. Интегралы от неограниченной функции.  Несобственные интегралы второго рода, признаки их сходимости.   Первый и второй достаточные признаки сходимости и расходимости несобственных интегралов II – го рода. Понятие числового ряда, общий член ряда, частичная сумма. Сходящийся и расходящийся числовой ряд. Сумма числового ряда.  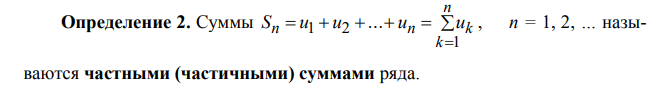   Основные свойства числовых рядов. Умножение числового ряда на число. Сумма числовых рядов. Отбрасывание k первых членов числового ряда.???   Гармонический ряд. Обобщенный гармонический ряд.    Необходимый признак сходимости числового ряда и его следствие.  Достаточные признаки сходимости числового знакоположительного ряда: признаки сравнения, признак Даламбера.    Возможно пригодится  Достаточные признаки сходимости числового знакоположительного ряда: радикальный признак Коши, интегральный признак Коши.  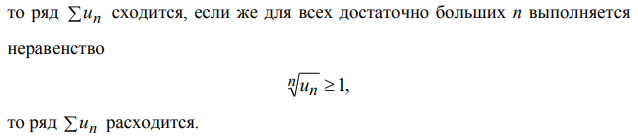 Возможно пригодится   Возможно пригодится  Знакопеременный и знакочередующийся числовой ряд. Признак Лейбница для знакочередующегося числового ряда. Числовой ряд 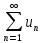 , члены которого имеют произвольные знаки «+» и «-», называется знакопеременным рядом.Знакочередующийся ряд – частный случай знакопеременного ряда, вида:    Абсолютная и условная сходимость знакопеременного числового ряда. Признак абсолютной сходимости знакопеременного числового ряда.    Возможно пригодится  Функциональный ряд, точки сходимости и расходимости функционального ряда, область сходимости функционального ряда. Сумма функционального ряда.   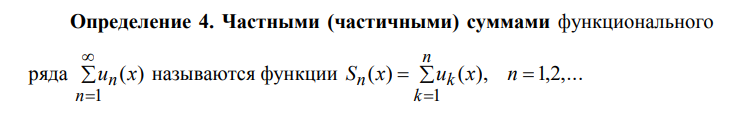  Степенной ряд. Интервал и радиус сходимости степенного ряда. Сумма степенного ряда. 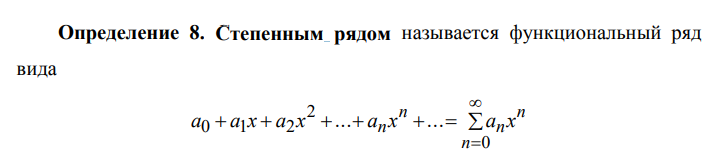  Сумма степенного ряда S: 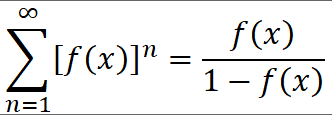 при  Возможно пригодится:     Если n в знаменателе, то 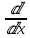 (дифференцируем)Если n в числителе, то 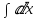 (интегрируем)Равномерная сходимость. Признак равномерной сходимости функционального ряда.  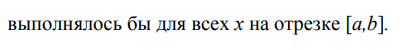  Интегрирование и дифференцирование функциональных рядов. Абсолютная сходимость функционального ряда. 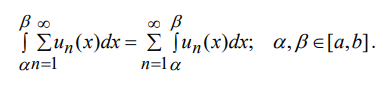 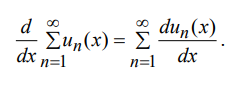   Разложение функций в степенные ряды. Ряды Тейлора и Маклорена.  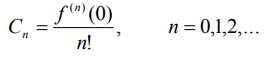  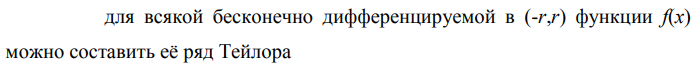 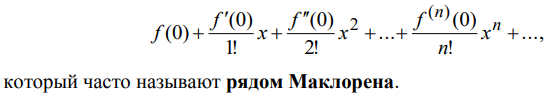  Возможно пригодится   Остаточный член ряда Тейлора. Приближенные вычисления с помощью рядов.  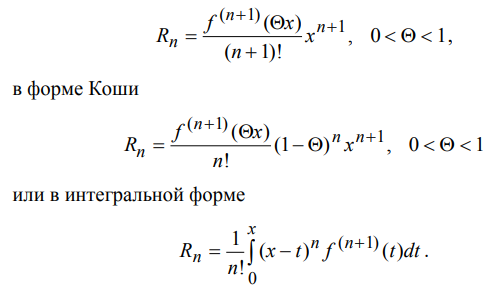  Тригонометрические ряды. Ряды Фурье. Коэффициенты ряда Фурье. 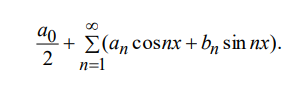  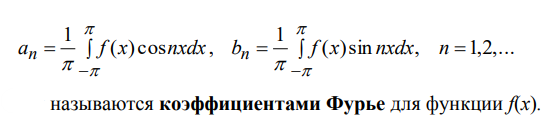  Теорема Дирихле. Разложение в ряд Фурье функций с периодом 2π.  Разложение в ряд Фурье функций с периодом 2l.  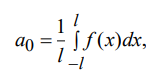 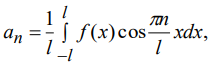 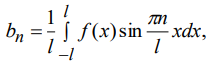  Разложение в ряд Фурье четных и нечетных функций.  Разложение в ряд Фурье функции, заданной в сегменте [0;l).  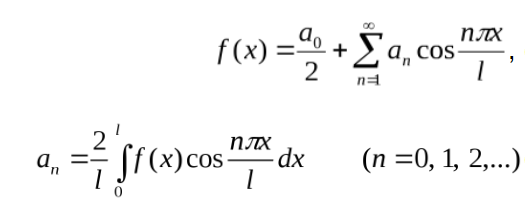  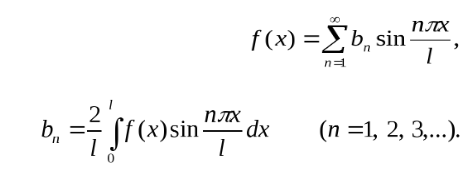  |