Архитектура ЭВМ. Архитектура ЭВМ 1. Ответы на контрольные вопросы
 Скачать 218.52 Kb. Скачать 218.52 Kb.
|
Ответы на контрольные вопросы
САНКТ-ПЕТЕРБУРГ 2023 г. СодержаниеСистема счисления 3 Схемные логические элементы ЭВМ : триггеры 8 Линейная, страничная, сегментная память 14 Базовые логические операции и схемы 16 Список использованных источников 18 1 Системы счисления Системой счисления (СС) называется способ изображения чисел с помощью ограниченного набора символов, имеющих определенные количественные значения. Систему счисления образует совокупность правил и приемов представления чисел с помощью набора знаков (цифр) [1]. Системы счисления подразделяются на позиционные и непозиционные, а позиционные, в свою очередь, — на однородные и смешанные. Непозиционная — самая древняя, в ней каждая цифра числа имеет величину, не зависящую от её позиции (разряда). То есть, если у вас 5 черточек — то число тоже равно 5, поскольку каждой черточке, независимо от её места в строке, соответствует всего 1 один предмет. Позиционная система — значение каждой цифры зависит от её позиции (разряда) в числе. Например, привычная для нас 10-я система счисления — позиционная. Рассмотрим число 453. Цифра 4 обозначает количество сотен и соответствует числу 400, 5 — количество десяток и аналогично значению 50, а 3 — единиц и значению 3. Как видим — чем больше разряд — тем значение выше. Итоговое число можно представить, как сумму 400+50+3=453. Однородная система — для всех разрядов (позиций) числа набор допустимых символов (цифр) одинаков. В качестве примера возьмем упоминавшуюся ранее 10-ю систему. При записи числа в однородной 10-й системе вы можете использовать в каждом разряде исключительно одну цифру от 0 до 9, таким образом, допускается число 450 (1-й разряд — 0, 2-й — 5, 3-й — 4), а 4F5 — нет, поскольку символ F не входит в набор цифр от 0 до 9. Смешанная система — в каждом разряде (позиции) числа набор допустимых символов (цифр) может отличаться от наборов других разрядов. Яркий пример — система измерения времени. В разряде секунд и минут возможно 60 различных символов (от «00» до «59»), в разряде часов – 24 разных символа (от «00» до «23»), в разряде суток – 365 и т. д. Первые предпосылки к появлению позиционной системы возникли в древнем Вавилоне. В Индии система приняла форму позиционной десятичной нумерации с применением нуля, а у индусов эту систему чисел заимствовали арабы, от которых её переняли европейцы. По каким-то причинам, в Европе за этой системой закрепилось название “арабская”. Десятичная система счисления – это одна из самых распространенных систем счисления. Именно её мы используем, когда называем цену товара и произносим номер автобуса. В каждом разряде (позиции) может использоваться только одна цифра из диапазона от 0 до 9. Основанием системы является число 10. Для примера возьмем число 503. Если бы это число было записано в непозиционной системе, то его значение равнялось 5+0+3 = 8. Но у нас — позиционная система и значит каждую цифру числа необходимо умножить на основание системы, в данном случае число “10”, возведенное в степень, равную номеру разряда. Получается, значение равно 5*102 + 0*101 + 3*100 = 500+0+3 = 503. Чтобы избежать путаницы при одновременной работе с несколькими системами счисления основание указывается в качестве нижнего индекса. Таким образом, 503 = 50310 [1]. Помимо десятичной системы, отдельного внимания заслуживают двоичная, восьмеричная, шестнадцатеричная системы. Двоичная система счисления — эта система, в основном, используется в вычислительной технике. Почему не стали использовать привычную нам 10-ю? Первую вычислительную машину создал Блез Паскаль, использовавший в ней десятичную систему, которая оказалась неудобной в современных электронных машинах, поскольку требовалось производство устройств, способных работать в 10 состояниях, что увеличивало их цену и итоговые размеры машины. Этих недостатков лишены элементы, работающие в двоичной системе. Тем не менее, рассматриваемая система была создана за долго до изобретения вычислительных машин и уходит “корнями” в цивилизацию Инков, где использовались кипу — сложные верёвочные сплетения и узелки. Двоичная позиционная система счисления имеет основание 2 и использует для записи числа 2 символа (цифры): 0 и 1. В каждом разряде допустима только одна цифра — либо 0, либо 1. Примером может служить число 101. Оно аналогично числу 5 в десятичной системе счисления. Для того, чтобы перевести из 2-й в 10-ю необходимо умножить каждую цифру двоичного числа на основание “2”, возведенное в степень, равную разряду. Таким образом, число 1012 = 1*22 + 0*21 + 1*20 = 4+0+1 = 510. Хорошо, для машин двоичная система счисления удобнее, но мы ведь часто видим, используем на компьютере числа в 10-й системе. Как же тогда машина определяет какую цифру вводит пользователь? Как переводит число из одной системы в другую, ведь в её распоряжении всего 2 символа — 0 и 1? Чтобы компьютер мог работать с двоичными числами (кодами), необходимо чтобы они где-то хранились. Для хранения каждой отдельной цифры применяется триггер, представляющий собой электронную схему. Он может находится в 2-х состояниях, одно из которых соответствует нулю, другое — единице. Для запоминания отдельного числа используется регистр — группа триггеров, число которых соответствует количеству разрядов в двоичном числе. А совокупность регистров — это оперативная память. Число, содержащееся в регистре — машинное слово. Арифметические и логические операции со словами осуществляет арифметико-логическое устройство (АЛУ). Для упрощения доступа к регистрам их нумеруют. Номер называется адресом регистра. Например, если необходимо сложить 2 числа — достаточно указать номера ячеек (регистров), в которых они находятся, а не сами числа. Адреса записываются в 8- и 16-ричной системах (о них будет рассказано ниже), поскольку переход от них к двоичной системе и обратно осуществляется достаточно просто. Для перевода из 2-й в 8-ю число необходимо разбить на группы по 3 разряда справа налево, а для перехода к 16-ой — по 4. Если в крайней левой группе цифр не достает разрядов, то они заполняются слева нулями, которые называются ведущими. В качестве примера возьмем число 1011002. В восьмеричной — это 101 100 = 548, а в шестнадцатеричной — 0010 1100 = 2С16. Отлично, но почему на экране мы видим десятичные числа и буквы? При нажатии на клавишу в компьютер передаётся определённая последовательность электрических импульсов, причём каждому символу соответствует своя последовательность электрических импульсов (нулей и единиц). Программа драйвер клавиатуры и экрана обращается к кодовой таблице символов (например, Unicode, позволяющая закодировать 65536 символов), определяет какому символу соответствует полученный код и отображает его на экране. Таким образом, тексты и числа хранятся в памяти компьютера в двоичном коде, а программным способом преобразуются в изображения на экране [2]. Восьмеричная система счисления Восьмеричная система счисления, как и двоичная, часто применяется в цифровой технике. Имеет основание 8 и использует для записи числа цифры от 0 до 7. Пример восьмеричного числа: 254. Для перевода в 10-ю систему необходимо каждый разряд исходного числа умножить на 8n, где n — это номер разряда. Получается, что 2548 = 2*82 + 5*81 + 4*80 = 128+40+4 = 17210. Шестнадцатеричная система счисления Шестнадцатеричная система широко используется в современных компьютерах, например при помощи неё указывается цвет: #FFFFFF — белый цвет. Рассматриваемая система имеет основание 16 и использует для записи числа: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B. C, D, E, F, где буквы равны 10, 11, 12, 13, 14, 15 соответственно. В качестве примера возьмем число 4F516. Для перевода в восьмеричную систему — сначала преобразуем шестнадцатеричное число в двоичное, а затем, разбив на группы по 3 разряда, в восьмеричное. Чтобы преобразовать число в 2-е необходимо каждую цифру представить в виде 4-х разрядного двоичного числа. 4F516 = (100 1111 101)2. Но в 1 и 3 группах не достает разряда, поэтому заполним каждый ведущими нулями: 0100 1111 0101. Теперь необходимо разделить полученное число на группы по 3 цифры справа налево: 0100 1111 0101 = 010 011 110 101. Переведем каждую двоичную группу в восьмеричную систему, умножив каждый разряд на 2n, где n — номер разряда: (0*22+1*21+0*20) (0*22+1*21+1*20) (1*22+1*21+0*20) (1*22+0*21+1*20) = 23658. В ЭВМ используется только двоичная С Восьмеричная и особенно шестнадцатеричная системы, являются производными от двоичной, поскольку их основания являются степенями числа 2. Используются они для более компактного отображения двоичной информации. 2 СХЕМНЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ ЭВМ: ТРИГГЕРЫ Триггером называется устройство, в любой момент времени находящееся только в одном из двух устойчивых состояний (0 либо 1). Он строится на логических элементах. Его можно классифицировать по различным признакам в соответствии с рисунком 2.1. 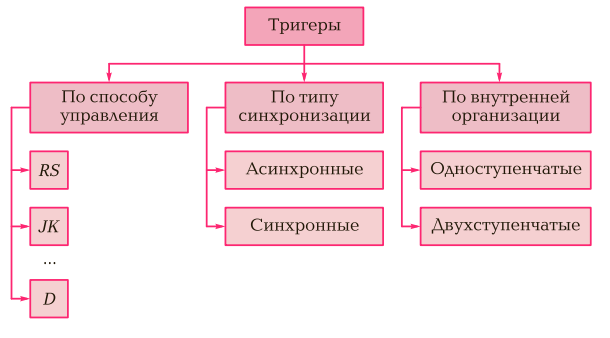 Рисунок 2.1 - Общая классификация триггеров По типу синхронизации триггеры подразделяются на асинхронные и синхронные. В асинхронных триггерах состояние на выходе изменяется сразу же после изменения сигнала на информационных входах. В синхронных триггерах для передачи сигнала с информационных входов на выходы требуется специальный синхронизирующий импульс на специальный вход C (как представлено на рисунке 2.2). 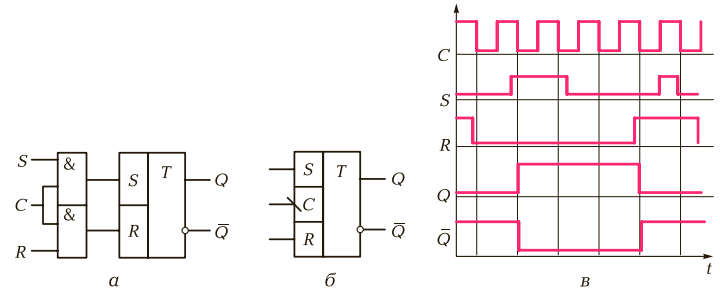 Рисунок 2.2 - Структурная схема (а), графическое обозначение (б) и временная диаграмма (в) синхронного RS-триггера По способу управления синхронные триггеры подразделяются на триггеры со статическим управлением и триггеры с динамическим управлением. В триггерах с динамическим управлением передача сигнала с информационных входов на выходы осуществляется по фронту или по спаду синхронизирующего импульса. По внутренней организации триггеры со статическим управлением подразделяются на одноступенчатые и двухступенчатые триггеры. Запись информации в одноступенчатые триггеры представляет собой непрерывный во времени процесс установления состояния триггера под воздействием информационных сигналов. Запись информации в двухступенчатые триггеры осуществляется в два этапа: сначала информация записывается в первую ступень, а затем переписывается во вторую и появляется на выходе триггера. В основе любого триггера лежит схема из двух логических элементов, которые охвачены положительными обратными связями (сигналы с выходов подаются на входы). В результате подобного включения схема может находиться в одном из двух устойчивых состояний, причем находиться сколь угодно долго, пока на нее подано напряжение питания. Если мы хотим хранить какую-либо двоичную последовательность цифр, то для каждой цифры следует использовать отдельный триггер. Для того чтобы получить данные о состоянии триггера, у него должна быть, по крайней мере, одна выходная линия, представляющая логическое значение, которое соответствует состоянию триггера. Когда на выходной линии логическая единица, говорят, что триггер установлен, в противном случае говорят, что триггер сброшен. Триггер имеет несколько входных линий. Последующее состояние триггера определяется текущим состоянием триггера и сигналами на входных линиях. Триггер обозначается прямоугольником, разделенным на основное и вспомогательное поля. В первом помещают букву T (триггер), во втором — условные обозначения (метки) входов и логических операций на входе. Логика работы определяется количеством входов и особенностями схемы. В зависимости от влияния, оказываемого на состояние триггера, его входы имеют следующие обозначения: S (Set-установка) — вход триггера для установки в состояние «1»; ƒƒ R (Reset-сброс) — вход триггера для установки в состояние «0»; J (Jump) — вход триггера для установки в состояние «1» в JКтриггере, а вход К (key) - для установки в состояние 0, т.е. входы J и К аналогичны входам S и R RS-триггера; K (Kill) — вход триггера для установки в состояние «0» в JКтриггере; ƒƒ D (Data input) — информационный вход. На него подается информация, предназначенная для записи в триггер; T (Toggle-переключатель) — счетный вход (если у триггера только счетный вход, букву не пишут); ƒƒ C (Clock input) — вход синхронизации. В отечественных сериях микросхем триггеры имеют наименование ТВ, ТМ и ТР в зависимости от типа триггера. Наиболее распространены три типа: ƒƒ RS-триггер (обозначается ТР) — самый простой триггер, но редко используемый; JK-триггер (обозначается ТВ) имеет самое сложное управление, также используется довольно редко; ƒƒ D-триггер (обозначается ТМ) — наиболее распространенный тип триггера. Простейшим из них является асинхронный RS-триггер (представлен на рисунке 2.3).  Рисунок 2.3 - Графическое обозначение асинхронного RS-триггера (а — с инверсными входами; б — с прямыми входами) и временная диаграмма (в) Кроме асинхронного RS-триггера существует синхронный RS-триггер рисунок 2.2. Синхронные триггеры снабжаются дополнительным входом, по которому поступает синхронизирующий (тактирующий) сигнал. При этом изменение состояния триггера происходит (при наличии управляющего сигнала) только в те моменты времени, когда на специальный синхровход триггера поступает тактирующий импульс. Синхронизирующий вход обозначается буквой С. Входные сигналы, по которым происходит переключение триггера: S и R — информационные и С — синхронизирующие. Все триггеры с синхронизирующим входом, которые управляются уровнем синхронизирующего сигнала, являются триггерами со статическим управлением. Схемы RS-триггеров являются одноступенчатыми. Применение одноступенчатых RS-триггеров в качестве самостоятельных запоминающих элементов ограничено. Большей востребованностью пользуются двухступенчатые триггеры (MS-триггеры) (представлен на рисунке 2.4) 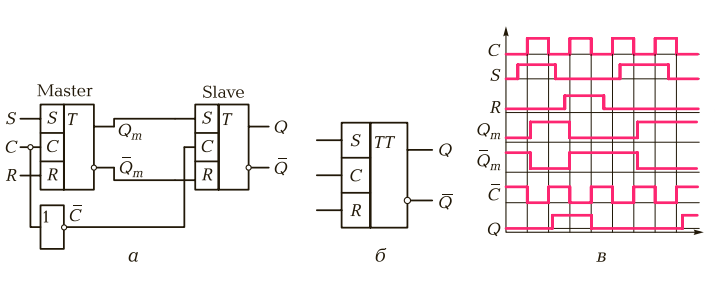 Рисунок 2.4 - Структурная схема (а), графическое обозначение (б) и временная диаграмма (в) MS-триггера Для построения двухступенчатых триггеров используются одноступенчатые RS-триггеры. Двухступенчатый триггер состоит из двух каскадных секций (ступеней), причем каждая секция содержит по синхронному RS-триггеру. Первая секция, ведущая или М-секция (Master) принимает информацию с входных линий S и R. Состояние выходов ведущей секции подается на вторую секцию, ведомую, или S-секцию (от англ. Slave). Если в обозначении синхронного RS-триггера с динамическим управлением стрелка на входе C направлена к триггеру, то передача сигналов с информационных входов на выходы происходит по фронту импульса, а если стрелка направлена от обозначения триггера, то передача сигнала осуществляется по спаду импульса. 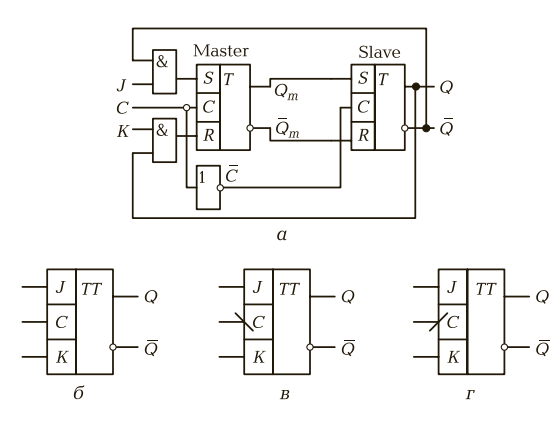 Рисунок 2.5 - JK-триггер со статическим управлением: а — структурная схема; б — графическое обозначение; графическое обозначение JK-триггера с динамическим управлением: в — по заднему фронту; г — по переднему фронту. Для устранения недостатка RS-триггеров (режим неопределенности при R = S = 1) применяются динамические JK-триггеры с более широкими функциональными возможностями. JK-триггер можно синтезировать (построить) на базе MS-триггера. D-триггер (от англ. Delay). Схемное обозначение D-триггера приведено на рисунке 2.6. 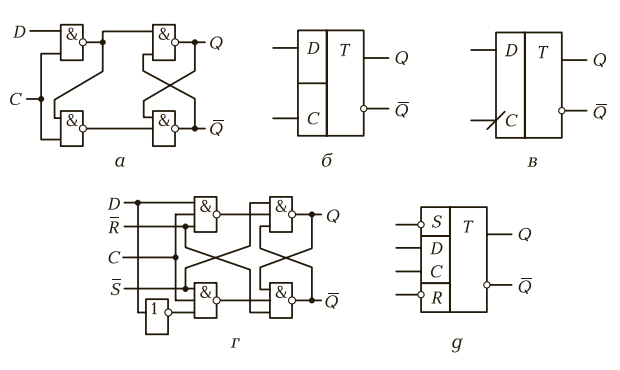 Рисунок 2.6 - D-триггер со статическим управлением (а — структурная схема; б — графическое обозначение); с динамическим управлением (в — графическое обозначение); с асинхронными инверсными входами установки и сброса S и R (г — структурная схема; д — графическое обозначение). Он обладает двумя устойчивыми состояниями и имеет, как минимум, две входные линии: информационный вход D (Dаtа) и вход управления записью (защелкиванием) L (Load или Latch) — отсюда его второе имя: «защелка». Последний вход часто обозначают символом C(lock). D-триггер называют информационным триггером, а также триггером задержки. D-триггер бывает только синхронным. Для триггера типа D состояние в интервале времени между сигналом на входной линии и следующим состоянием триггера формируется проще, чем для любого другого типа. Если на вход S подать 0, а на вход R — сигнал 1, то Q = 1 и Q = 0 независимо от сигналов на остальных входах. Триггер устанавливается в единицу. Сигналы D и C не влияют на этот процесс. В силу этого, асинхронные входы (S и R) имеют наивысший приоритет. Так как асинхронные связи симметричны, при S = 1 и R = 0 триггер сбрасывается (Q = 0). 3 ЛИНЕЙНАЯ, СТРАНИЧНАЯ, СЕГМЕНТНАЯ ПАМЯТЬ Линейная адресация памяти — схема адресации памяти компьютера в Intel-совместимых процессорах, начиная с Intel 80386. Благодаря введению механизма линейной адресации можно создавать любое (ограниченное только размерами оперативной памяти) количество адресных пространств. Причём каждая страница линейного адресного пространства может находиться по любому (естественно, выравненному по границе 4 КБайт) физическому адресу, а благодаря обработчику #PF — и на любом накопителе [3]. Страничная память — способ организации виртуальной памяти, при котором единицей отображения виртуальных адресов на физические является регион постоянного размера (т. н. страница). Типичный размер 4096 байт, для некоторых архитектур до 128 КБ. Поддержка такого режима присутствует в большинстве 32битных и 64битных процессоров. Такой режим является классическим для почти всех современных ОС, в том числе Windows и семейства UNIX. Широкое использование такого режима началось с процессора VAX и ОС VMS с конца 70х годов (по некоторым сведениям, первая реализация). В семействе x86 поддержка появилась с поколения 386, оно же первое 32битное поколение. Сегментная адресация памяти — схема логической адресации памяти компьютера в архитектуре x86. Линейный адрес конкретной ячейки памяти, который в некоторых режимах работы процессора будет совпадать с физическим адресом, делится на две части: сегмент и смещение. Сегментом называется условно выделенная область адресного пространства определённого размера, а смещением — адрес ячейки памяти относительно начала сегмента. Базой сегмента называется линейный адрес (адрес относительно всего объёма памяти), который указывает на начало сегмента в адресном пространстве. В результате получается сегментный (логический) адрес, который соответствует линейному адресу база сегмента+смещение и который выставляется процессором на шину адреса. Селектором называется число (в x86 — 16-битное), однозначно определяющее сегмент. Селектор загружается в сегментные регистры. В реальном и защищённом режимах x86-процессора функционирование сегментной адресации отличается [4]. 4 БАЗОВЫЕ ЛОГИЧЕСКИЕ ОПЕРАЦИИ И СХЕМЫ Логическая переменная имеет только два значения ("истина" и "ложь"). В алгебре логики их обозначают как "1" и "0" и называют логической единицей и логическим нулем. Существуют три основные операции над переменными: -инверсия (логическое отрицание, функция НЕ); -дизъюнкция (логическое сложение, функция ИЛИ); - конъюнкция (логическое умножение, функция И). Алгебра логики определяется следующей системой аксиом: x = 0, если х≠1, ō= 1, x = 1, если х≠0, ī= 0, 1+ 1 = 1, 0 * 0 = 0, 0 + 0 = 0, 1 * 1 = 1, 0 + 1 = 1 + 0 = 1, 1 * 0 = 0 * 1 + 0 Логические выражения связывают значение логической функции со значениями логических переменных. Они могут записываться или в конъюнктивной или дизъюнктивной нормальных формах. В дизъюнктивной форме логические выражения записываются как логическая сумма логических произведений, в конъюнктивной – как логическое произведение логических сумм. Порядок действий в логических выражениях такой же, как и в обычных алгебраических выражениях. Логические выражения связывают значение логической функции со значениями логических переменных. Основные логические функции могут быть реализованы с помощью электронных схем, называемых логическими элементами. Условные графические обозначения элементов и соответствующие им таблицы истинности приведены на рисунке 4.1-4.3. 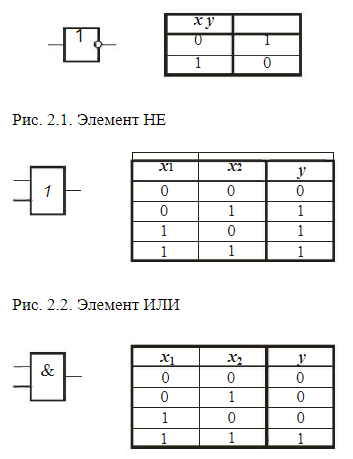 Рисунок 4.1 - Элемент НЕ 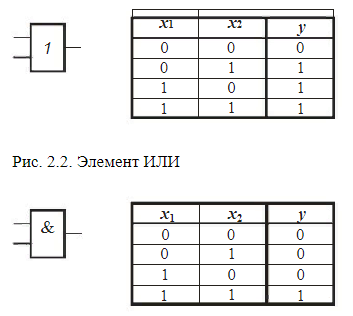 Рисунок 4.2 - Элемент ИЛИ  Рисунок 4.3 - Элемент И СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВЗемсков А.И., Шрайберг Я.Л. Электронные библиотеки: учебник для вузов. – М: Либерия, 2003 – 351 с. Костюк К.Н. Книга в новой медицинской среде. – М.: Директ – Медиа, 2015. – 430 с. Линейная, страничная, сегментная память [Электронный ресурс]. –URL: (дата обращения 06. 01.2023). Бесперстов Э.А. Исследование логических схем с использованием программного комплекса Multisim: лабораторный практикум. – СПб: БГТУ, 2006. Перечень сокращений и обозначений: Cc: (копия, carbon copy) — вторичные получатели письма, которым направляется копия. Они видят и знают о наличии друг друга. Bcc: (скрытая копия, blind carbon copy) — скрытые получатели письма, чьи адреса не показываются другим получателям. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

