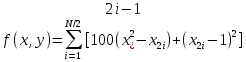Алгоритм рыбьей стаи. П. В. Христенко ты лучше шаришь, что тут целью проекта является развитие и коммерциализация технологии нечеткого моделирования и идентификации. Ключевые слова алгоритм рыбьей стаи, метаэвристика, задача
 Скачать 120.05 Kb.
|
|
Применение алгоритма РЫБЬЕЙ СТАИ для решения задач оптимизации П.В. Христенко ТЫ ЛУЧШЕ ШАРИШЬ, ЧТО ТУТ Целью проекта является развитие и коммерциализация технологии нечеткого моделирования и идентификации. Ключевые слова: алгоритм рыбьей стаи, метаэвристика, задача оптимизации. Постановка задачи: Множество практических задач зачастую сводятся к решению общей задачи оптимизации. Формально, проблема минимизации целевой функции может быть записана следующим образом:  Здесь за  обозначено множество допустимых значений переменных, также называемое пространством поиска, в подавляющем большинстве случаев являющееся подмножеством некоторого множества действительных чисел.Существует значительное множество подходов к решению упомянутой задачи. Наиболее эффективными являются методы, основанные на использовании информации о градиенте функции а так же о производных высших порядков. Такие методы быстры и эффективно реализуемы на ЭВМ, но накладывают некоторые ограничения на оптимизируемую функцию и пространство поиска. Так, от функции требуется как минимум непрерывность и дифференцируемость почти всюду, а от пространства поиска связность и замкнутость. Так же данные методы зачастую останавливаются при нахождении локальных минимумов, что требует осторожности при решении задач, имеющих несколько различных локальных минимумов. Для решения более общей задачи, в случае невозможности наложения на целевую функцию столь жестких условий существуют различные эвристические методы, основанные на поведении различных сущностей из реального мира, таких как стаи животных или атомы в затвердевающем кристалле. В данной работе рассматривается алгоритм искусственной рыбьей стаи, в оригинале называющийся «Artifisial fish swarm». Алгоритм рыбьей стаи: Поведение стаи основано на соблюдении баланса между желанием каждой рыбки переместиться в позицию с наилучшей концентрацией пищи в пределах области зрения вокруг, необходимостью всех рыбок не расходиться слишком далеко от центра стаи, и желанием не успешных рыбок отделиться на значительное удаление от центра. Поведение стаи описывается следующими константами:  - радиус зрения единичной рыбки,  - максимальная длина шага в выбираемом направлении,  - предельная допустимая плотность соседей для каждой рыбки,  - длина шага при смене пространства поиска,  - число попыток на стадии охоты.1. (Prey): Для каждой рыбки, расположенной в позиции  выбирается произвольная точка в в радиусе зрения рыбки  . В случае, если значение целевой функции в новой точке более выгодно, чем в текущей , то есть  выполняется перемещение  и переход к пункту 2. Попытка совершения шага совершается  раз, после всех неудач выполняется единственный шаг в произвольную точку в области видимости:  и переход к пункту 2.2. (Swarm): Вычисляется центр стаи как среднее арифметическое координат ее членов  , после чего для каждой рыбки выполняется перемещение на случайный шаг в сторону центра:  .3. (Follow): Для каждой рыбки  вычисляется  - локальная плотность стаи как отношение числа членов стаи, находящихся в области зрения к общему размеру стаи. В случае, если  выполняется шаг охоты (1, Prey), Иначе находится сосед из области зрения  с наилучшим значением целевой функции и выполняется шаг в его сторону:  4. (Move): Каждая рыбка произвольно перемещается в области своего зрения: 5. (Leap): В случае, если за последние несколько шагов найденное наилучшее значение целевой функции изменилось менее чем на  (или в возможной реализации вообще не изменилось) то выбирается произвольная рыбка  и выполняется ее перемещение  .Шаги 1-5 выполняются по количеству итераций алгоритма. В приведенной реализации функция  возвращает случайную величину из равномерного распределения на  , а функция  - точку из равномерного распределения на шаре единичного радиуса в пространстве той размерности, в котором выполняется оптимизация.Эксперимент: Первый эксперимент проводился в двумерном пространстве, поиск производился на квадрате  , в качестве гиперпараметров выбраны  , число итераций равно 200
Таблица 1 – Результаты эксперимента для пространства размерности 2 Второй эксперимент проводился в десятимерном пространстве, поиск производился на квадрате  в качестве гиперпараметров выбраны , число итераций равно 200 и 2000
Таблица 1 – Результаты эксперимента для пространства размерности 10 Как можно видеть, алгоритм начинает испытывать значительные трудности при увеличении размерности пространства поиска. Заключение: В результате эксперимента было выявлено, что алгоритм в некоторых случаях позволяет находить значения, близкие к минимуму, но качество работы зависит от многих внешних факторов, таких как выбор гиперпараметров или размерность целевого пространства ЛИТЕРАТУРА: ВСТАВЬ ПО ГОСТУ |
