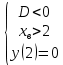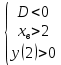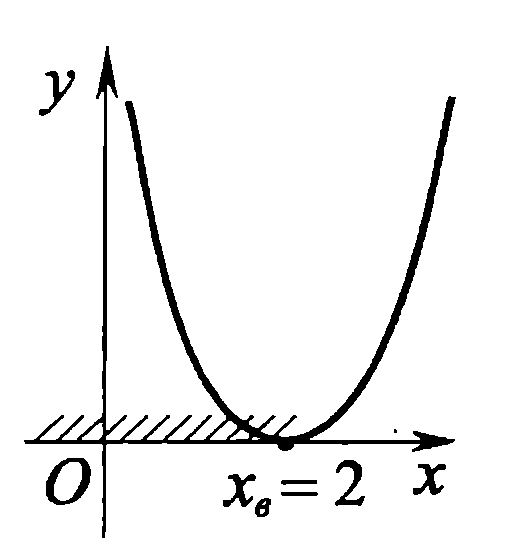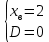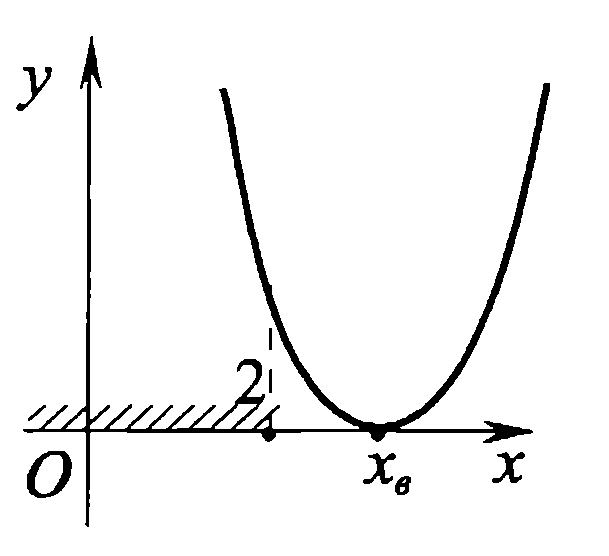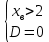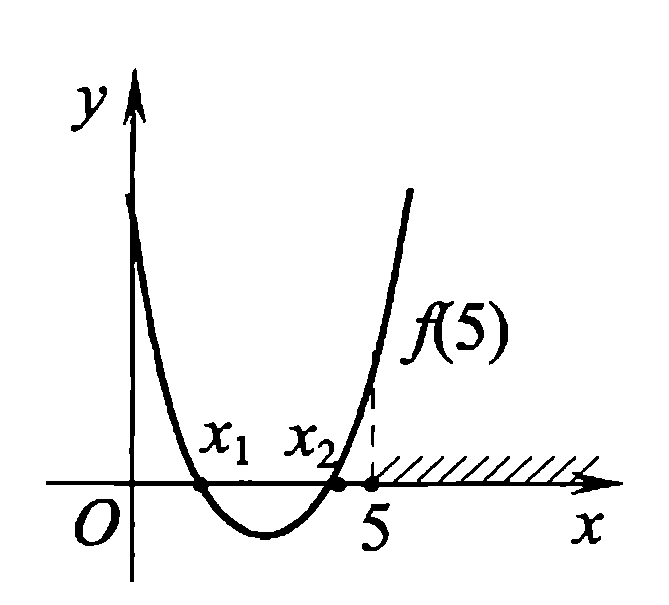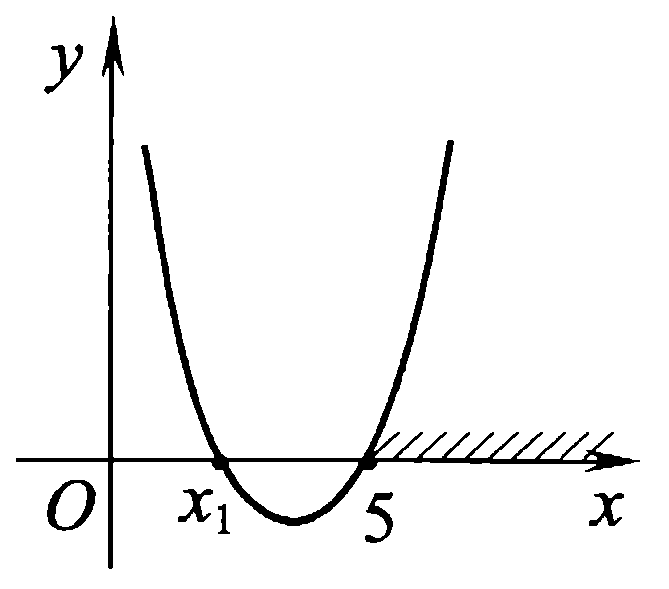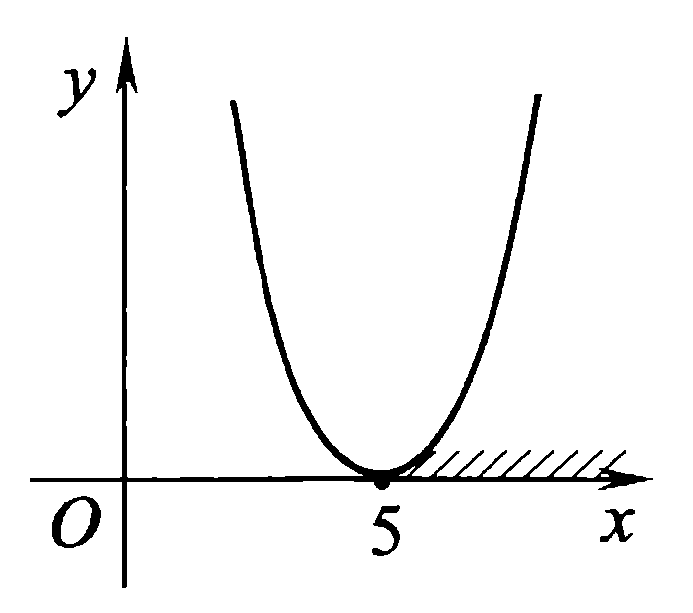Квадратные неравенства с параметрами. Параметры 2 Квадратные неравенства 5 Структура квадратных неравенств 7 Графический метод 10 Аналитический метод 11 Примеры задач квадратных неравенств с параметром 12 Задача
 Скачать 279.55 Kb. Скачать 279.55 Kb.
|
ОглавлениеВведение 1 Параметры 2 Квадратные неравенства 5 Структура квадратных неравенств 7 Графический метод 10 Аналитический метод 11 Примеры задач квадратных неравенств с параметром 12 Задача 1. 12 Задача 2 13 Задача 3. 13 Задача 4. 14 Задача 5 15 Задача 6 15 Заключение 18 Список литературы 19 ВведениеМатериал школьного курса математики, который связан с неравенствами содержащие параметры, является важным звеном. Задачи с параметрами важны, так как теоретическое и практическое изучение разнообразных процессов в различных областях науки и профессиональной деятельности людей часто приводят к решению уравнений, неравенств, систем, содержащие параметры с различным уровнем сложности. При решении таких задач следует с большой точностью изучить характер и конечный результат на основе значений параметров. Часто оказывается, что решение задачи зависит не только от каждого параметра отдельно, а от некоторых их совместных характеристик. Эти задачи требуют понимания сути процесса, овладения различными методами и приемами. Кроме того, проблемы с параметрами относятся к классу проблем, в которых алгоритмы либо не существуют, либо неприменимы. Эти задачи требуют умения проводить логические, иногда обширные и самостоятельные построения. Начиная с 8-го класса учащиеся ежедневно сталкиваются с квадратичными уравнениями и неравенствами, и поэтому овладение методами и навыками решения квадратичных уравнений и неравенств с параметрами должно подтолкнуть преподавателей на подробное изучение этого материала. Также задачи с параметрами являются одним из заданий в контрольно-измерительных материалах Единого государственного экзамена уровня профиля, в решении которого могут возникнуть некие сложности, это связано с такими особенностями как: – большое количество формул и методов, используемых при решении уравнений данного вида; – возможность решения одного и того же уравнения различными методами [1]. В ходе курсовой работы будут рассмотрены квадратичные неравенства с параметрами, примеры и методы решения таких задач. ПараметрыПараметр является величиной, значения которых служит для различных элементов множества между собой. Исследования многих систем, процессов осуществляется при помощи использования параметров. Например, если для динамического тела указан закон движения, то его положение можно определить с помощью параметра времени. Для функции 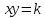 в качестве параметром является в качестве параметром является 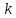 обратной пропорциональности. Общим для этих примеров является выделение неких характеристик систем, по изменениям которых может быть проведена оценка состояния всей системы. В математике параметры вводятся для обозначения совокупности объектов. Например, уравнение обратной пропорциональности. Общим для этих примеров является выделение неких характеристик систем, по изменениям которых может быть проведена оценка состояния всей системы. В математике параметры вводятся для обозначения совокупности объектов. Например, уравнение 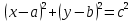 с параметрами с параметрами 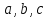 определяют совокупность всех окружностей, функции определяют совокупность всех окружностей, функции 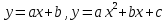 определяют бесконечное множество частных функций для конкретных значений параметров определяют бесконечное множество частных функций для конкретных значений параметров 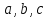 . Общее исследование аще всего сводится к классификации частных функций с одинаковыми свойствами, это может быть область определения, область значений или монотонность. Также параметрами могут быть функциями какой-либо переменной . Общее исследование аще всего сводится к классификации частных функций с одинаковыми свойствами, это может быть область определения, область значений или монотонность. Также параметрами могут быть функциями какой-либо переменной 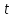 вида вида 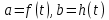 . .Параметр, как характеристика системы, множества объектов может быть величиной или принимать постоянные значения – быть константой. Главной особенностью задач с параметрами является ветвление решений в зависимости от значений параметров. То есть процесс решения осуществляется через классификация частных неравенств по типам с последующим поиском общего решения для каждого типа. В основе этой классификации лежит теория равносильных преобразований уравнений и неравенств, теоремы о граничных значениях параметров. Одновременное решение бесконечного множества частных неравенств с учетом требований равносильности преобразований возможно только при выработке умений и развитии достаточного уровня логического мышления. Формирование этих умений может обеспечить прогресс в развитии математической культуры учащихся, который определяется следующими факторами. Множество различных типов частных уравнений, неравенств, которые требуют владения соответствующими методами решения, использования теоретических фактов. Этим обеспечивается актуализация знаний многих разделов математики. При решении задач с параметрами проводится исследование частных типов уравнений или неравенств и поиск общего способа решения. Поиск каждого этапа в общем решении формирует исследовательские умения, которые востребованы в науке. Решение неравенств с параметрами является процессом равносильных преобразований для значений параметров из какой-либо области. Образы областей граничных значений являются обязательной частью логических рассуждений в ходе исследования. Использование графических изображений в качестве ориентира формирует отличный теоретический способ усвоения знаний. Внедрение задач с параметрами в содержание школьного курса математики определяется использованием неравенств и уравнений с параметрами в практике итоговых и вступительных экзаменов [2]. В таблице 1 представлены различные виды параметризации уравнений и неравенств [3]. Таблица 1. Виды параметризации уравнений и неравенств
Квадратные неравенстваПрименимость квадратных уравнений и неравенств исходит с времен древности. Необходимость решать уравнения первой и второй степени вызвана потребностью решать задачи, связанные с определением площадей земельных участков и с работами военного характера, с развитием математики, астрономии и физики. Понятие «больше» или «меньше» вместе с понятием равенства возникли из-за необходимости сравнения величин. Квадратные уравнения используются при решении многих задач, неравенств второй степени, дробно-рациональных, при решении биквадратных, тригонометрических, показательных, иррациональных уравнений и неравенств. В школьном курсе изучаются формулы корней квадратного уравнения, с помощью которых можно рационально решать квадратные уравнения и неравенства. 1. Метод интервалов, приводящий решение неравенство стандартного вида к решению уравнения, то есть, нахождению нулей функции с последующим определением знаков функции на промежутках ее знакопостоянства. 2. Способ решения квадратных неравенств с помощью графика квадратичной функции. 3. Метод решения квадратных неравенств с помощью «схематичного» построения параболы. Существует множество способов решения уравнений и квадратных неравенств, однако, не все из них легко решить, но каждый из них по-своему уникален. Некоторые методы решения экономят время при решении задач на контрольных работах и экзаменах [4]. При изучении неравенств и их систем учащиеся должны хорошо разбираться в разных видах числовых промежутках, их записи, названиях, обозначениях и изображениях на координатной прямой. Ниже (таб.2) представлено обозначение числовых промежутков, их названия и изображение [5]. Таблица 2. Обозначение числовых промежутков
Также следует познакомиться с неравенствами, которые содержат неизвестное под знаком модуля, которые являются одним из трудных неравенств. Для решения подобных неравенств необходимо знать понятие модуля числа и умение его применять – модуль положительного числа равен самому числу, модуль отрицательного числа равен противоположному числу, модуль нуля равен нулю. Символически определение модуля записывается как 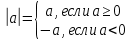 Если значение под модулем положительно, то знак модуля в неравенстве пропускается, в противном случае (значение под модулем отрицательное) модуль «опускается», изменив знак выражения на противоположный [6]. Структура квадратных неравенствКвадратными (строгими и нестрогими) называются неравенства вида: 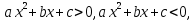 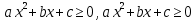 Квадратные неравенства с параметром можно решать как аналитически, так и графически. Графиком квадратичной функции является парабола, при 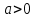 ветви параболы направлены вверх, а при ветви параболы направлены вверх, а при 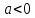 вниз. Расположение зависит от значений, которые принимает дискриминант [7]. вниз. Расположение зависит от значений, которые принимает дискриминант [7].Для того, чтобы оба корня квадратного трехчлена 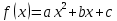 были больше некоторого числа были больше некоторого числа 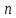 необходимо и достаточно выполнение следующих условий: необходимо и достаточно выполнение следующих условий: 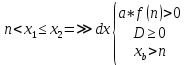 Для того, чтобы парабола пересекала ось Ох в точках 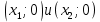 , лежащих правее точки , лежащих правее точки 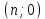 необходимо и достаточно выполнения трех условий: необходимо и достаточно выполнения трех условий:Вершина параболы лежит в нижней полуплоскости, либо в верхней полуплоскости, либо на оси Ох Ось симметрии параболы прямая 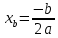 лежит правее прямой лежит правее прямой 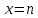 Парабола пересекается с прямой 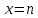 в точке, лежащей в нижней полуплоскости, при в точке, лежащей в нижней полуплоскости, при 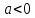 Для того, чтобы оба корня квадратного трехчлена 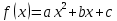 были больше некоторого числа были больше некоторого числа 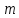 необходимо и достаточно выполнение следующих условий: необходимо и достаточно выполнение следующих условий: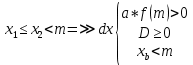 Для того, чтобы оба корня квадратного трехчлена 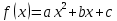 принадлежали некоторому заданному промежутку принадлежали некоторому заданному промежутку 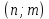 необходимо и достаточно выполнение следующих условий: необходимо и достаточно выполнение следующих условий: 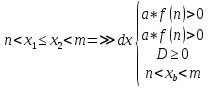 Только меньший корень квадратного трехчлена 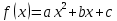 принадлежит заданному промежутку принадлежит заданному промежутку 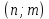 тогда и только тогда, когда выполняются одновременно условия: тогда и только тогда, когда выполняются одновременно условия: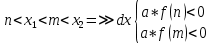 Только больший корень квадратного трехчлена 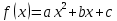 принадлежит заданному промежутку принадлежит заданному промежутку 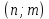 тогда и только тогда, когда выполняются одновременно условия: тогда и только тогда, когда выполняются одновременно условия: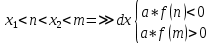 Квадратный трехчлен 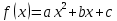 имеет один корень внутри интервала имеет один корень внутри интервала 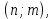 а другой расположен вне этого интервала тогда и только тогда, когда выполняется условие а другой расположен вне этого интервала тогда и только тогда, когда выполняется условие 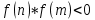 . .Квадратный трехчлен 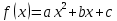 имеет два корня, расположенные по одному на каждом из двух непересекающихся интервалов имеет два корня, расположенные по одному на каждом из двух непересекающихся интервалов 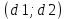 и и 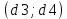 тогда и только тогда, когда одновременно выполняются условия: тогда и только тогда, когда одновременно выполняются условия: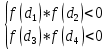 [8]. [8].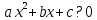 при разных значениях при разных значениях 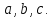
Аналогично определяется множество решений, если 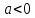
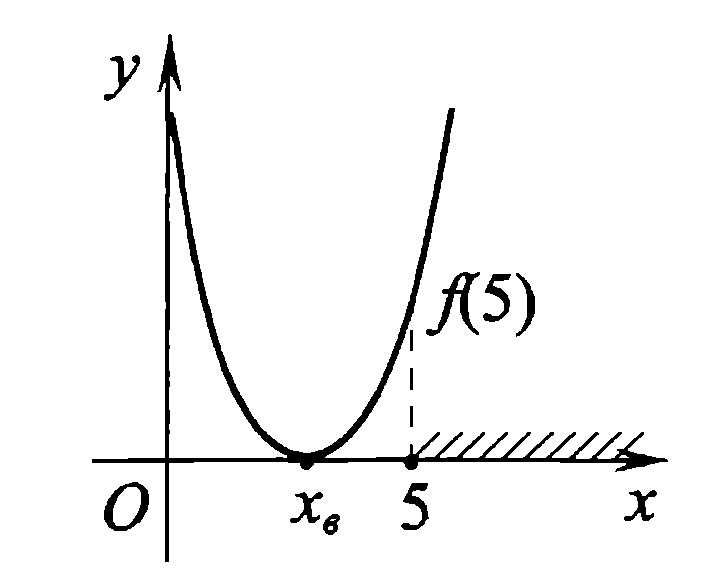
Задач на решение квадратных неравенств с параметрами может быть нескольких типов. Первым типом являются задачи, в которых требуется найти значения параметра, при котором неравенство: 1) выполняется при любом значении 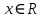 ; ; 2) выполняется ровно для одного значения 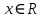 ; ; 3) не выполняется ни для одного значения 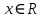 . .Решение этих задач основывается на исследовании знака дискриминанта и знака старшего коэффициента при 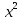 . .Вторым типом являются задачи, в которых задано множество М, отличное от R, нужно найти значения всех параметров, при которых квадратное неравенство будет выполняться на множестве М. Решение задачи заключается в нахождении необходимого расположения корней квадратного трехчлена относительно множества М, в последующем, которое будет описано в виде неравенства. Решение этих неравенств позволяет найти требуемые значения параметров [9]. Графический методГрафический метод является одним из основным методов решения любых уравнений и неравенств, при этом в образовательной программе школьного курса математики он занимает низкую позицию. В силу своей наглядности, он по праву может быть назван наиболее рациональным и эффективным. Поэтому необходимо постоянно применять графический метод для решения задач квадратных неравенств с параметрами [10]. Алгоритм решения квадратных неравенств состоит из следующих действий: Определение направление ветвей параболы по знаку коэффициента в квадратичной функции – 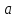 Нахождение действительных корней соответствующего квадратного уравнения или их отсутствие Изображение графика квадратичной функции, используя точки пересечения или касания с осью Ох Определение по графику промежутков, на которых функция принимаем нужные значения Аналитический метод Аналитический метод является прямым способом решения, который повторяет процедуры нахождения решения задачи квадратных неравенств без параметра, так как под параметром подразумевают какое-то число, которое может менять свое значение или оставаться постоянным. Аналитический метод решения задач с параметром предоставляет возможность получить ответ с наиболее вероятной точностью, что является преимуществом перед другими методами. Но также этот метод имеет свои недостатки, потому что требует высокого уровня математических знаний и грамотности, что преподносит его как один из самых трудоемких методов по сравнению с другими [11]. Некоторые задачи на исследование квадратного трехчлена решаются с помощью теоремы Виета: В квадратном уравнении 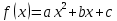 , где , где 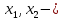 корни, сумма корней равна соотношению коэффициентов корни, сумма корней равна соотношению коэффициентов 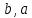 , которое было взято с противоположным знаком, а произведение корней будет равно отношению коэффициентов , которое было взято с противоположным знаком, а произведение корней будет равно отношению коэффициентов 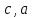 т.е. т.е. 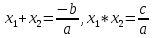 . Коэффициент при квадрате должен быть единицей - . Коэффициент при квадрате должен быть единицей - 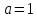 [12]. [12].Приведем схему исследования задач, связанных с расположением корней квадратного трехчлена  : :1. Исследование случая  (если первый коэффициент зависит от а). (если первый коэффициент зависит от а).2. Нахождение дискриминанта 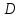 в случае в случае 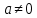 . .3. Если 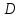 — полный квадрат некоторого выражения, то нахождение корней — полный квадрат некоторого выражения, то нахождение корней 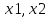 и подчинение условиям задачи. и подчинение условиям задачи.4. Если 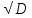 — не извлекается, то графический анализ задачи (геометрическая модель). — не извлекается, то графический анализ задачи (геометрическая модель).5. Аналитическое описание подходящих случаев расположения параболы, для чего учитываются: знак коэффициента при х2, знак дискриминанта, знаки квадратичной функции в изучаемых точках, расположение вершины параболы относительно изучаемых точек (аналитическая модель). 6. Объединение получаемых неравенств и составление системы или систем неравенств 7. Решение полученных систем Примеры задач квадратных неравенств с параметромЗадача 1.При каких значениях параметра а неравенство 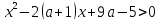 выполняется при всех значениях х. выполняется при всех значениях х.Решение: а=1, ветви параболы, направлены вверх. В зависимости от знака дискриминанта возможны три варианта:
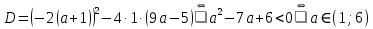 Ответ: 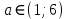 Задача 2При каких значениях параметра а неравенство 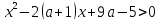 не выполняется ни для одного значения не выполняется ни для одного значения 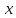 . .Решение:
Ответ: таких 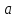 нет нетЗадача 3.При каких р неравенство 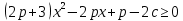 а) выполняется при всех х; б) не выполняется ни для одного значения х; в) выполняется ровно для одного значения х Решение:
Ответ: а) 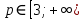 б) 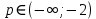 в) p=-2 Задача 4.При каких значениях параметра а неравенство 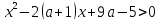 выполняется при всех значениях х<2. выполняется при всех значениях х<2.Решение:
Ответ: 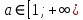 Задача 5При каких значениях параметра а неравенство 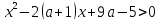 выполняется при всех значениях х≥5. выполняется при всех значениях х≥5.Решение:
Ответ: 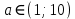 Задача 6При каких значениях параметра а неравенство 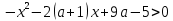 выполняется при всех значениях 1<х≤4. выполняется при всех значениях 1<х≤4.Решение:
Ответ: 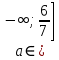 . .Задача 7 При каких значения параметра 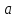 уравнение уравнение 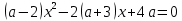 имеет два корня, один из которых меньше 2, а другой больше 3? имеет два корня, один из которых меньше 2, а другой больше 3?Решение: Первый способ. Так как речь идет о двух корнях, то рассматриваемое уравнение должно быть квадратным, т.е. 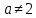 . .Рассмотрим функцию 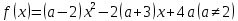 Ее графиком является парабола, кото рая по условию задачи пересекает ось 0х один раз на интервале 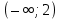 и один раз на интервале и один раз на интервале 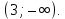 Рассмотрим два случая: 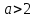 и и 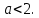 В первом случае получим систему неравенств: 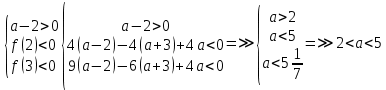 Во втором случае получим систему: 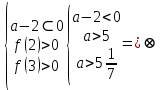 Второй способ. Для того, чтобы оба корня данного квадратного трехчлена лежали вне заданного промежутка, необходимо и достаточно выполнение условий 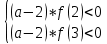 Получим систему неравенств: 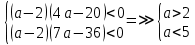 Ответ: 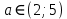 ЗаключениеСовременный этап развития школьного математического образования характеризуется приоритетом разработки учебных целей. В связи с этим при изучении математики, организованном обучении методам мышления особое значение имеет рациональное выполнение учебной деятельности, что чрезвычайно важно при освоении сложных предметов и решении сложных задач, таких как уравнения и неравенства с параметрами. Именно отсутствие подготовки к методам учебной деятельности является одной из причин, по которой большинство учеников допускают ошибки или испытывают трудности с решением даже простых задач такого типа. Кроме того, внедрение выпускных экзаменов в новой форме (использовании) в практику российской школы требует от студентов обучения методикам решения основных видов математических задач (в том числе с параметрами), по возможности в обобщенной форме, что позволяет студентам переносить изученные методики в новые нестандартные ситуации, поскольку меняются тестовые задания, практически невозможно решить все их разновидности или предсказать возможные варианты[13]. В школьном классе математики важной частью является материал, связанный с уравнениями и неравенствами, и это не случайно. При их поддержке на символическом языке записываются важные задачи, связанные со знанием реальной реальности. Уравнения и неравенства сопровождают учащихся при изучении каждого предмета в виде углубления, обновления и расширения теоретических знаний. Операции над числами и свойствами этих операций, функциями и свойствами функций, метрическими отношениями между элементами геометрических фигур, тождествами и трансформациями тождеств, а также для решения проблем содержания жизни, связанных с вопросами современного производства, экономики народного хозяйства со смежными дисциплинами и т. д. Задача с параметром, по мнению П. М. Эрдниева – это естественный шаг в решении любой математической задачи [14]. Часть параметрических задач состоит в том, чтобы найти корни квадратного уравнения, расположенные определенным образом относительно заданной точки или интервала. В этом случае целесообразно использовать графический метод из-за его наглядности. Использованию графического метода должен предшествовать тщательный анализ того, как парабола может быть расположена в соответствии с условиями задачи. В этом случае стоит обратить внимание на следующие моменты: знак дискриминанта, знаки квадратного уравнения в характерных точках, таких как, например, концы отрезков, расположение вершины параболы через определенные промежутки времени. Когда все это улажено, учащиеся легко смогут решить квадратные параметрические уравнения [15]. Список литературыНуну Е.И. Квадратные уравнения с параметрами // Студенческая наука и XXI век. – № 13. – 2016. – С. 33-35. Горбачев В.И. Элементы теории и общие методы решения уравнений и неравенств с параметрами – г. Брянск. – 1998. – С. 264. Фалилеева М.В. Методические аспекты обучения решению уравнений и неравенств с параметрами // Фундаментальные исследования. – № 4-5. – 2013. – С. 1230-1235 Хужаева А.Р. Проблема обучения школьников решению квадратных уравнений и неравенств // Актуальные проблемы современного образования. – № 8(30). – 2021. – С. 124-132. Титоренко С.А., Константинова О.А. Решение одной из задач ЕГЭ по математике на квадратные неравенства с параметром // Некоторые вопросы анализа, алгебры, геометрии и математического образования. – № 8. – 2018. – С. 314-315. [Электронный ресурс] – Режим доступа: https://skysmart.ru/articles/mathematic/modul-chisla Магомедов И.М. Решение квадратных уравнений с параметрами – пропедевтика научно-исследовательской работы учащихся // Образование в современной школе. – №3. – 2010. – С.33-52 Белова М.С. Формирование приемов решения неравенств и их систем у учащихся 8 класса основной школы // Современные тренды математики и математического образования. – Саранск. – 2020. [Электронный ресурс] – Режим доступа: https://nsportal.ru/shkola/algebra/library/2014/10/25/reshenie-kvadratnykh-neravenstv-s-parametrom Ковылина А.А. Визуализация решения квадратных неравенств с помощью приема «пазл» //Актуальные вопросы математического образования: состояние, проблемы и перспективы развития. – Сургут. – 2019. – С. 69-73. Колбов А.Н. Аналитический метод решения в различных видах уравнений и неравенств с параметрами // Университетский комплекс как региональный центр образования, науки и культуры. – Оренбург. – 2021. С. 1625-1632. [Электронный ресурс] – Режим доступа: https://zaochnik.com/spravochnik/matematika/vyrazhenija/teorema-vieta-formuly-vieta/ Арюткина С.В. О формировании обобщенных приемов математической деятельности у учащихся средней школы (на примере приемов решения квадратных уравнений с параметром) // Математический вестник Педвузов и университетов Волго-Вятского региона. – № 11. – 2009. – С. 264-273. Амерева Д.Ю., Фрундин В.Н. Развитие творческого мышления при решении уравнений и неравенств с параметрами в 10-11 классах // наука и образование: отечественный и зарубежный опыт. – Белгород. – 2020. – С. 50-58. Варенцова Н.А. К вопросу о задачах с параметрами в средней школе // Научный поиск. – №2.1 – 2014. – С.30-31. |

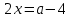
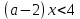
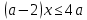
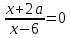
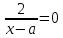
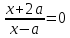
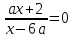
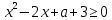
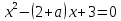
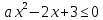
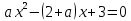
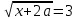
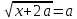
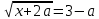
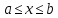
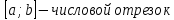

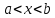
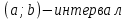

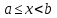
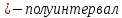

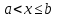
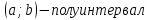

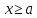
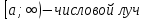

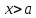
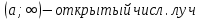

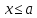
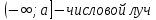

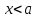
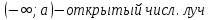

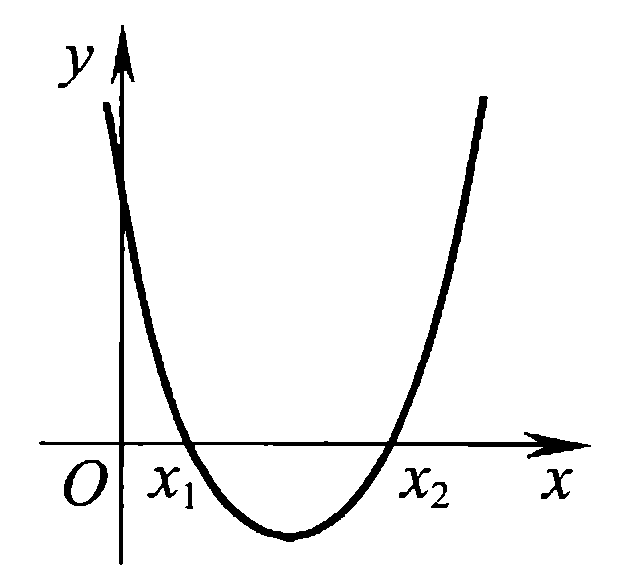
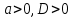
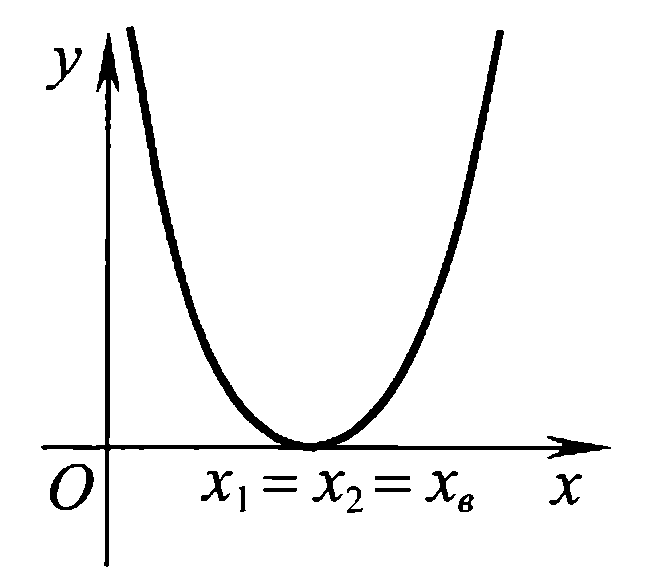
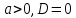
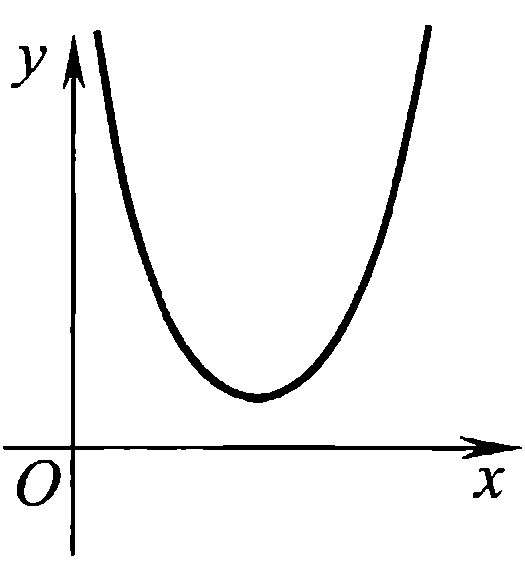
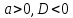
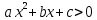
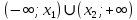
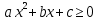
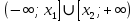
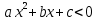
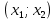 ш:
ш: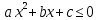
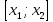
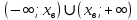
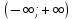
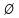
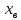
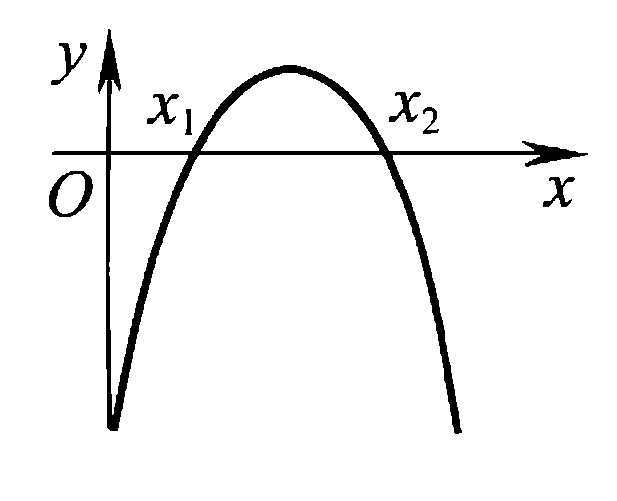
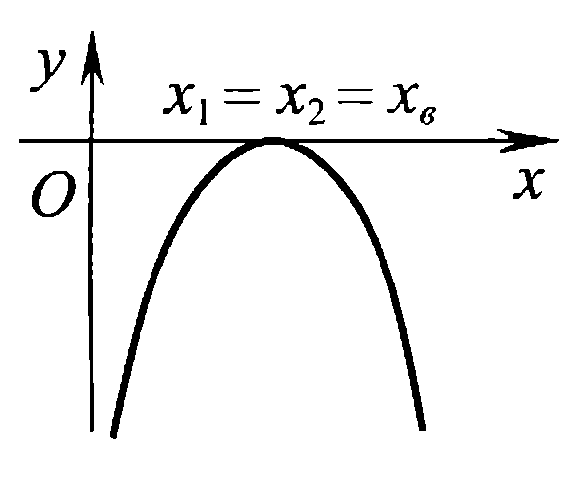
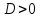
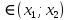 значение у<0
значение у<0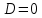
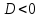
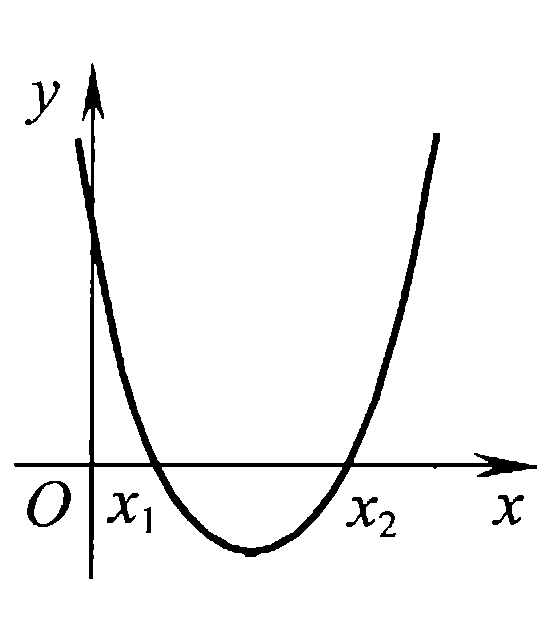
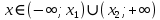 выполняется y>0
выполняется y>0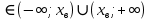 у>0
у>0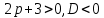
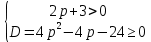
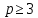
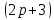 <0, D>0
<0, D>0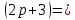 0
0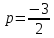 , то
, то 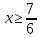
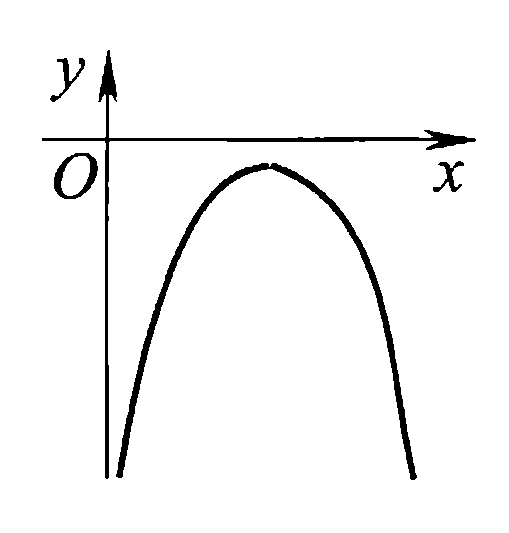
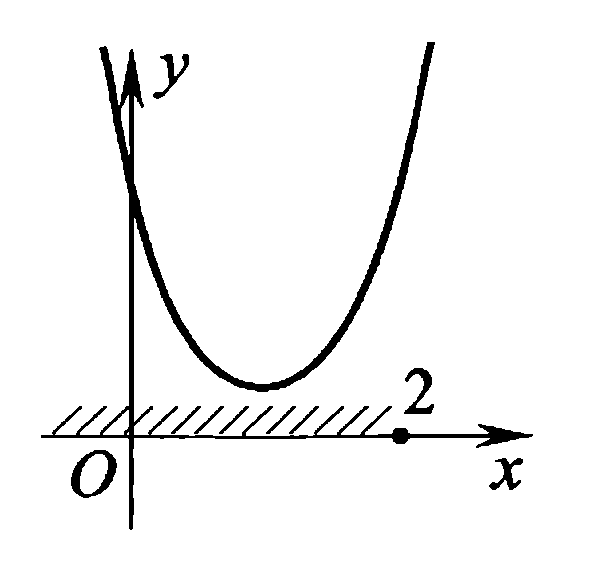
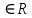 , т.е. при х<2
, т.е. при х<2