элементы цепей переменного тока. Практика Параметры переменного тока и напряжения. Параметры переменного тока и напряжения
 Скачать 204.24 Kb.
|
|
Параметры переменного тока и напряжения Количественными показателями для измерений и расчётов переменного тока являются следующие параметры: Период T - время, в течении которого происходит один полный цикл изменения тока в оба направления относительно нуля или среднего значения. Частота f - величина, обратная периоду, равная количеству периодов за одну секунду. Один период в секунду это один герц (1 Hz). Частота f = 1/T Циклическая частота ω - угловая частота, равная количеству периодов за 2π секунд. ω = 2πf = 2π/T Обычно используется при расчётах тока и напряжения синусоидальной формы. Тогда в пределах периода можно не рассматривать частоту и время, а исчисления производить в радианах или градусах. T = 2π = 360° Начальная фаза ψ - величина угла от нуля (ωt = 0) до начала периода. Измеряется в радианах или градусах. Показана на рисунке для синего графика синусоидального тока. 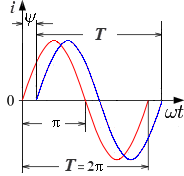 Начальная фаза может быть положительной или отрицательной величиной, соответственно справа или слева от нуля на графике. Мгновенное значение - величина напряжения или тока измеренная относительно нуля в любой выбранный момент времени t. i = i(t); u = u(t) Последовательность всех мгновенных значений в любом интервале времени можно рассмотреть как функцию изменения тока или напряжения во времени. Например, синусоидальный ток или напряжение можно выразить функцией: i = Iampsin(ωt); u = Uampsin(ωt) С учётом начальной фазы: i = Iampsin(ωt + ψ); u = Uampsin(ωt + ψ) Здесь Iamp и Uamp - амплитудные значения тока и напряжения. Амплитудное значение - максимальное по модулю мгновенное значение за период. Iamp = max|i(t)|; Uamp = max|u(t)| Может быть положительным и отрицательным в зависимости от положения относительно нуля. Часто вместо амплитудного значения применяется термин амплитуда тока (напряжения) - максимальное отклонение от нулевого значения. Среднее значение (avg) - определяется как среднеарифметическое всех мгновенных значений за период T.  Среднее значение является постоянной составляющей DC напряжения и тока. Для синусоидального тока (напряжения) среднее значение равно нулю. Средневыпрямленное значение - среднеарифметическое модулей всех мгновенных значений за период. 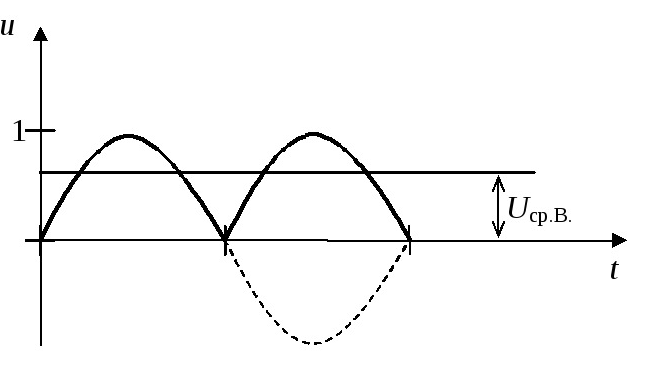  Для синусоидального тока или напряжения средневыпрямленное значение равно среднеарифметическому за положительный полупериод.  Среднеквадратичное значение (rms) - определяется как квадратный корень из среднеарифметического квадратов всех мгновенных значений за период. 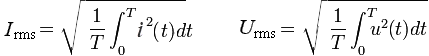 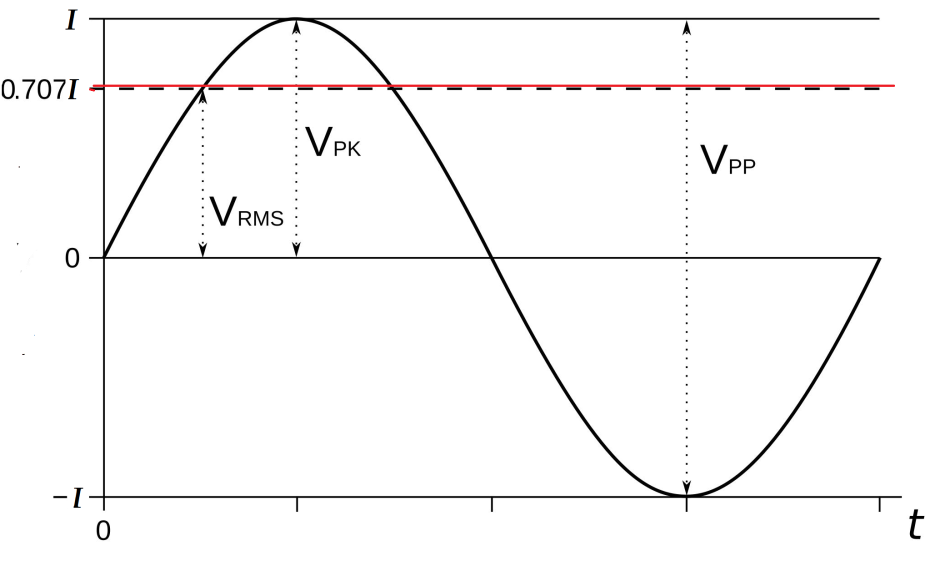 Для синусоидального тока и напряжения амплитудой Iamp (Uamp) среднеквадратичное значение определится из расчёта: 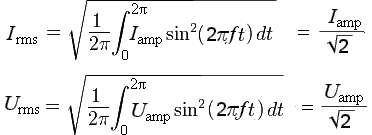 Среднеквадратичное - это действующее, эффективное значение, наиболее удобное для практических измерений и расчётов. Является объективным количественным показателем для любой формы тока. В активной нагрузке переменный ток совершает такую же работу за время периода, что и равный по величине его среднеквадратичному значению постоянный ток. Коэффициент амплитуды и коэффициент формы Для удобства расчётов, связанных с измерением действующих значений при искажённых формах тока, используются коэффициенты, которыми связаны между собой амплитудное, среднеквадратичное и средневыпрямленное значения. Коэффициент амплитуды - отношение амплитудного значения к среднеквадратичному. 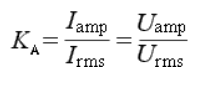 Для синусоидального тока и напряжения коэффициент амплитуды KA = √2 ≈ 1.414 Коэффициент формы - отношение среднеквадратичного значения к средневыпрямленному. 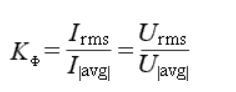 Для переменного синусоидального тока или напряжения коэффициент формы KФ ≈ 1.111 Векторная диаграмма Расчеты в цепях с синусоидальными напряжениями и токами весьма упрощаются, если вместо синусоид оперировать с их изображениями — вращающимися векторами. Пусть NOM является прямоугольной системой осей координат и пусть положительные углы откладываются против направления вращения стрелки часов. Если нужно найти, например, мгновенные значения синусоиды э. д. с.  то для этого можно взять вектор ОА, длина которого равна в выбранном масштабе максимальному значению э. д. с. 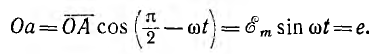 считать начальным положением вектора ОА0 такое, при котором он образует с осью ON угол, равный начальной фазе, т. е. в данном случае совпадает с 0N: вращать этот вектор в положительном направлении с постоянной угловой скоростью, равной угловой частоте ω. Тогда угол, который вектор образует с осью ON в момент времени е, будет равен ωt и мгновенное значение э.д.с. е для этого момента времени будет равно проекции Оа вектора ОА на ось ОМ: Проекция вектора ОА на ось ОМ для начального момента времени  будет равна нулю, для момента времени, когда вектор повернется на угол π/2, проекция будет равна 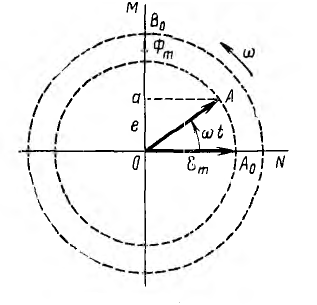 полный цикл изменений э. д. с. получится за один полный оборот вектора ОА. Задачи 1. По графику найти амплитудное значение переменной ЭДС, ее период и частоту. Записать формулу изменения ЭДС со временем. 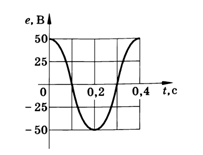 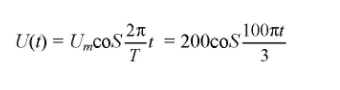 2. При вращении проволочной рамки в однородном магнитном поле пронизывающий рамку магнитный поток изменяется в зависимости от времени по закону Ф = = 0,01 sin 10πt. Вычислив производную Ф', написать формулу зависимости ЭДС от времени е = e(t). В каком положении была рамка в начале отсчета времени? Какова частота вращения рамки? Чему равны максимальные значения магнитного потока и ЭДС? 3. Уравнение для силы тока имеет вид: i=4.5sin(100t+ π/2 ) (A) Найти амплитудное Imax и эффективное Iэф значение силы тока, частоту тока f, начальную фазу тока . Построить векторную диаграмму для силы тока |