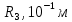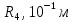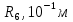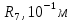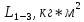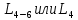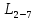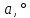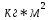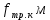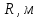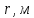пв. Документ Microsoft Office Word. Параметры редукторов
 Скачать 104.71 Kb. Скачать 104.71 Kb.
|
 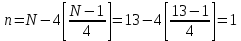 Параметры редукторов
Параметры поднимаемого груза
Для подъема и перемещения груза применяют механизм, называемый грузовой лебедкой, которая состоит из двигателя, ведущего вала 1, планетарного редуктора, ведомого вала 2, барабана и троса (см. рис. 3.6). Двигатель, редуктор и барабан лежат на одной оси, поднимаемый груз Q находится на наклонной плоскости с углом наклона α Лебедка приводится в движение двигателем. Ведущему валу двигателя сообщается постоянный вращательный момент 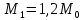 удерживает систему в покое, и его величину рассчитывают в процессе решения задачи). (момент удерживает систему в покое, и его величину рассчитывают в процессе решения задачи). (момент 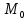 удерживает систему в покое, и его величину рассчитывают в процессе решения задачи). удерживает систему в покое, и его величину рассчитывают в процессе решения задачи).Планетарный редуктор предназначен для передачи крутящего момента от двигателя непосредственно к приводу. Редуктор состоит из набора взаимно зацепленных зубчатых колес с перемещающимися осями, которые, в свою очередь, способны вращаться вокруг неподвижных осей. Одно из колес в редукторе установлено неподвижно. Так как подвижные шестерни движутся вокруг одного центра, то вся конструкция напоминает солнечную систему, и поэтому редуктор называется планетарным, а подвижные шестерни – сателлитами. Груз Q поднимается по наклонной плоскости без скольжения, коэффициент трения качения тр.к. 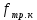 . Силы сопротивления, приложенные к механизму редуктора условно приводятся к моменту . Силы сопротивления, приложенные к механизму редуктора условно приводятся к моменту 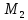 , приложенному к ведомому валу, величина которого принимается пропорциональной угловой скорости вала: , приложенному к ведомому валу, величина которого принимается пропорциональной угловой скорости вала: 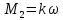 . .Определить: 1) используя теорему об изменении кинетической энергии для механической системы: дифференциальное уравнение движения ведущего вала 1; закон изменения угловой скорости вала 1, движущегося из состояния покоя до установившегося движения. Привести график этой зависимости; угловую скорость установившегося движения; 2) используя теорему об изменении кинетического момента системы: силы взаимодействия между двумя сцепленными шестернями (по выбору) закон изменения натяжения троса в зависимости от времени и его установившееся значение; 3) из уравнений движения груза по наклонной плоскости силу реакции наклонной плоскости; коэффициент трения скольжения, обеспечивающий качение груза по наклонной плоскости без скольжения Кинематический расчет редуктора. В редукторе (рис. 3.1) вращение ведущего вала с угловой скоростью ω1 передается на ведомый вал 2 следующим образом. Водило 3, вращаясь с угловой скоростью ω1, приводит в движение систему шестерен 4, 6, закрепленных на общей оси 4-6. Шестерня 4 находится в зацеплении с неподвижной (опорной) шестерней 5 корпуса редуктора. Подвижные шестерни 4, 6 совершают спинное движение: вращаясь вокруг оси 4-6 (относительное движение), вместе с этой осью вращение переносится водилом вокруг центральной оси 1-2 редуктора (переносное движение); шестерня 6, находясь в зацеплении с шестерней 7, приводит в движение ведомый вал 2. v 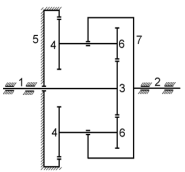 Рис. 3.1. Схема редуктора и крепление барабан Расчет кинематики редуктора проводится методом мгновенного центра скоростей. Пусть угловая скорость ведомого вала 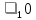 . Мгновенная ось абсолютного вращения шестерен 4, 6 проходит параллельно центральной оси 1-2 через точку касания K неподвижной шестерни 5 и подвижной шестерни 4. Эта точка K является мгновенным центром скоростей. Так как в рассматриваемой конструкции редуктора мгновенный центр скоростей располагается за осью относительного движения 4-6, то скорость относительного движения шестерен 4, 6 . Мгновенная ось абсолютного вращения шестерен 4, 6 проходит параллельно центральной оси 1-2 через точку касания K неподвижной шестерни 5 и подвижной шестерни 4. Эта точка K является мгновенным центром скоростей. Так как в рассматриваемой конструкции редуктора мгновенный центр скоростей располагается за осью относительного движения 4-6, то скорость относительного движения шестерен 4, 6 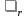 по абсолютной величине больше скорости переносного движения по абсолютной величине больше скорости переносного движения 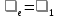 и угловая скорость абсолютного вращения и угловая скорость абсолютного вращения 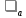 будет направлена в сторону большей из угловых скоростей (т.е. в сторону будет направлена в сторону большей из угловых скоростей (т.е. в сторону 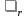 ) и будет равна ) и будет равна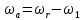 (3.1) (3.1)Точка K делит расстояние между осями переносного 1-2 и относительного 4-6 движений внешним образом на части, обратно пропорциональные значениям угловых скоростей: 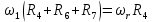 или 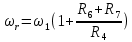 (3.2) (3.2)Из (3.1) и (3.2) находим скорость абсолютного вращения: 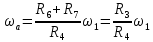 (3.3) (3.3)Для определения угловой скорости вращения шестерни 7, и следовательно, и угловой скорости ведомого вала 2 воспользуемся тем, что абсолютные скорости точек шестерен 6 и 7 в точке С их зацепления равны между собой, поскольку нет относительного проскальзывания: 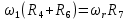 Таким образом, 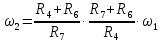 (3.4) (3.4)Передаточное число редуктора 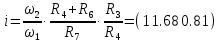 В том случае, если мгновенный центр скоростей располагается между осями переносного и относительного движений (рис. 3.2), то мгновенная ось абсолютного вращения делит расстояние между осями переносного и относительного движений внутренним образом на части, обратно пропорциональные модулям угловых скоростей, скорость результирующего движения равна сумме угловых скоростей составляющих движений.  Рис. 3.2. Редуктор, в котором мгновенная ось вращения шестеренки 6 располагается между осями переносного и относительного движений Таким образом, для редуктора, изображенного на рис. 3.2, Расчет кинетической энергии системы. Кинетическая энергия редуктора вместе с барабаном складывается из энергии ведущего вала и водила 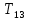 , энергии спаренной шестерни , энергии спаренной шестерни 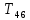 , энергии шестерни 7, вала 2 и барабана , энергии шестерни 7, вала 2 и барабанаВодило и вал 1 вращаются вокруг неподвижной оси и их кинетическая энергия 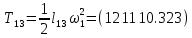 Шестерни 4-6 совершают сложное движение. Поэтому кинетическую энергию шестеренок 4 и 6 найдем как половину произведения момента инерции относительно мгновенной оси вращения и квадрата абсолютной угловой скорости, которую вычисляют по формуле (3.3). Момент инерции относительно мгновенной оси вращения определяется с помощью теоремы Штейнера 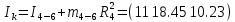 В итоге, 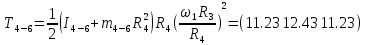 Шестерня 7 с ведомым валом и барабаном вращаются вокруг неподвижной оси и их кинетическая энергия равна 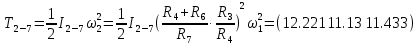 Суммарная кинетическая энергия лебедки 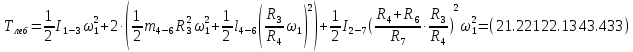 Кинетическая энергия груза определяется по теореме Кенига (рис. 3.3) 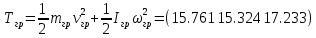 где 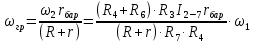 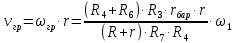 (3.5) (3.5)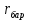 - радиус барабана. - радиус барабана.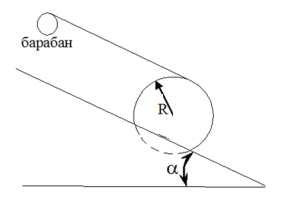 Рис. 3.3. Барабан и поднимаемый груз (вид сбоку) Кинетическая энергия системы равна сумме кинетических энергий лебедки и груза: 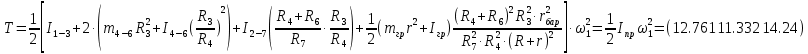 (3.6) Где 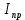 – приведенный моментом инерции. – приведенный моментом инерции.Вычисление элементарной работы сил, действующих на систему. Работа сил на элементарном перемещении при движении груза без проскальзывания (рис. 3.4) складывается из работы момента, приложенного к барабану, 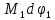 , работы момента сопротивления в редукторе, условно приведенного ко второму валу, , работы момента сопротивления в редукторе, условно приведенного ко второму валу, 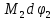 ,работы силы тяжести груза ,работы силы тяжести груза 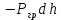 , где , где 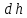 – элементарное изменение высоты центра тяжести груза, работы момента трения качения, действующего на груз, – элементарное изменение высоты центра тяжести груза, работы момента трения качения, действующего на груз, 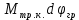 где где 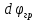 – элементарный угол поворота груза. Все элементарные перемещения, на которых совершается работа, вызваны поворотом вала – элементарный угол поворота груза. Все элементарные перемещения, на которых совершается работа, вызваны поворотом вала 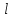 (см. рис. 3.1). (см. рис. 3.1).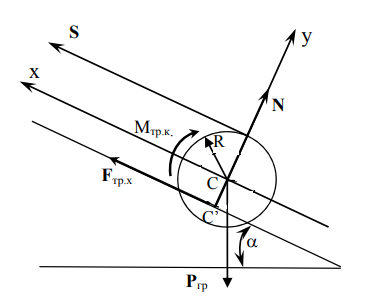 Рис. 3.4. Плоское движение груза Таким образом, 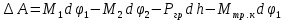 Отметим, что только работа момента 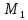 входит с положительным знаком в работу входит с положительным знаком в работу 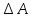 , так как моменты , так как моменты 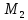 , , 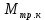 и сила и сила 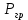 имеют отрицательную мощность. Из соотношений (3.4) и (3.5) имеют отрицательную мощность. Из соотношений (3.4) и (3.5)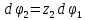 , , 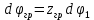 , , 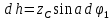 здесь 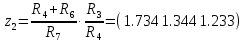 , 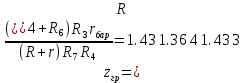 , , 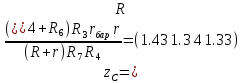 (3.7) (3.7)и, следовательно, 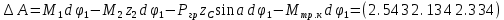 Момент 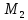 по условию пропорционален угловой скорости по условию пропорционален угловой скорости 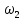 : :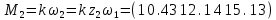 Момент трения качения 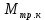 определяется по закону определяется по закону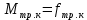 где N – нормальная составляющая реакции наклонной плоскости на груз. Для ее нахождения требуется рассмотреть уравнения плоскопараллельного движения груза: 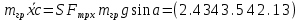 (3.8) (3.8)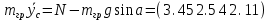 (3.9) (3.9)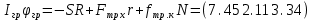 (3.10) (3.10)Так как 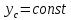 , то , то 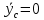 и, следовательно, из уравнения (3.9) и, следовательно, из уравнения (3.9)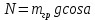 Для нахождения зависимости 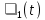 воспользуемся теоремой об изменении кинетической энергии. Cила воспользуемся теоремой об изменении кинетической энергии. Cила 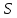 является внутренней силой системы и при нерастяжимости троса ее работа равна нулю. Дифференциал кинетической энергии в соответствии с выражением (3.6) имеет вид является внутренней силой системы и при нерастяжимости троса ее работа равна нулю. Дифференциал кинетической энергии в соответствии с выражением (3.6) имеет вид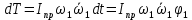  (3.11) (3.11)Формула (3.7) для элементарной работы переписывается следующим образом: 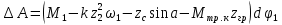  (3.12) (3.12)При равновесии 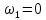 и и 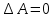 . При этом вместо момента . При этом вместо момента 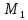 к первому валу прикладывается момент к первому валу прикладывается момент 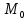 , который удерживает систему в равновесии. Следовательно, , который удерживает систему в равновесии. Следовательно,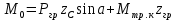 Далее по условию задачи 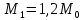 Подставим выражения (3.11) и (3.12) в теорему об изменении кинетической энергии 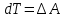 и сократим левую и правую части полученного выражения на и сократим левую и правую части полученного выражения на 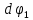 В результате этих действий записываем дифференциальное уравнение для определения угловой скорости первого валa В результате этих действий записываем дифференциальное уравнение для определения угловой скорости первого валa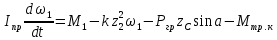 которое является дифференциальным уравнением с разделяющимися переменными и имеет аналитическое решение 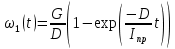 (3.13) (3.13)где 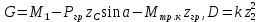 Натяжение свободного участка троса в зависимости от времени. Для нахождения силы натяжения троса S применим теорему об изменении кинетического момента для груза относительно мгновенного центра скоростей – точки 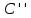 (см. рис. 3.4): (см. рис. 3.4):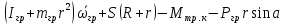 (3.14) (3.14)Здесь использовали теорему Штейнера для определения момента инерции относительно оси, проходящей через точку 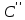 перпендикулярно плоскости рисунка. Зависимость величины перпендикулярно плоскости рисунка. Зависимость величины 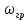 от времени известна, так как от времени известна, так как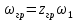 , где угловая скорость , где угловая скорость 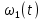 известна из формулы (3.13). Из формулы (3.14) находим величину силы S: известна из формулы (3.13). Из формулы (3.14) находим величину силы S: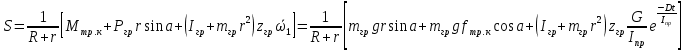 (3.15) (3.15)Определение силы реакции наклонной плоскости и коэффициента трения скольжения груза, обеспечивающего его подъем по наклонной плоскости без проскальзывания. Скорость точки контакта груза с плоскостью равна нулю: 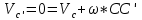 или в проекции на ось x 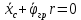 откуда следует 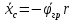 Уравнения плоского движения (3.8) и (3.10) с учетом зависимости Уравнения плоского движения (3.8) и (3.10) с учетом зависимости 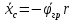 переписываем в виде переписываем в виде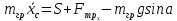 (3.16) (3.16)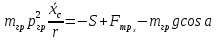 (3.17) (3.17)Здесь учтена зависимость 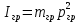 , где , где 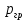 радиус инерции груза относительно оси, проходящей через его центр перпендикулярно рисунку. Из (3.17) получаем радиус инерции груза относительно оси, проходящей через его центр перпендикулярно рисунку. Из (3.17) получаем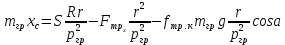 (3.18) (3.18)Так как левые части выражений (3.16) и (3.18) одинаковы, то равными должны быть и правые части этих соотношений 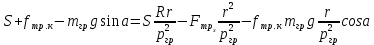 (3.19) (3.19)откуда 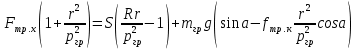 и окончательно 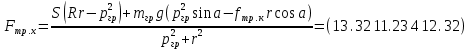 Условие отсутствия проскальзывания груза по наклонной плоскости 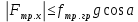 и, следовательно, 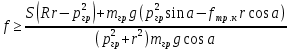 Напомним, что величина силы S определяется выражением (3.15). Силы взаимодействия между двумя шестернями редуктора. Взаимодействие между шестеренками 6 и 7 определим с помощью теоремы об изменении кинетического момента, которую составим относительно неподвижной оси, совпадающей с валом 2. Используем теорему об изменении кинетического момента относительно второго вала, с которым жестко соединена шестеренка 7 и барабан, на который наматывается трос. На шестеренку 7 со стороны шестерни 6 действует сила 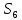 (рис. 3.5). Ко второму валу приложен момент сопротивления в редукторе (рис. 3.5). Ко второму валу приложен момент сопротивления в редукторе 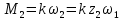 . Теорема об изменении кинетического момента позволяет записать дифференциальное уравнение . Теорема об изменении кинетического момента позволяет записать дифференциальное уравнение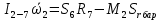 откуда 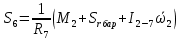 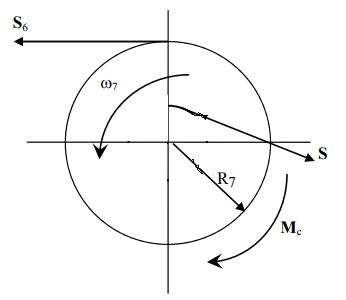 \Рис. 3.5. Усилия, действующие на шестеренку 7 Здесь сила 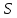 берется из формулы (3.15), момент берется из формулы (3.15), момент 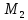 с учетом зависимости (3.13) равен с учетом зависимости (3.13) равен 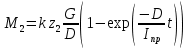 и, наконец, и, наконец,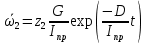 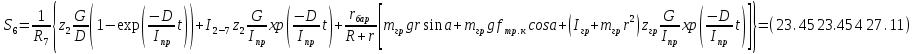 | ||||||||||||||||||||||||||||||||||||