Билеты. Билеты-ПДС. Передача дискретных сообщений
 Скачать 175.5 Kb. Скачать 175.5 Kb.
|
|
Вечерний факультет, специальность 2009, 5 курс, дисциплина "Передача дискретных сообщений". Билет 19 Группа: ФИО студента: Заданную двоичную последовательность 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 1 закодировать манчестерским кодом, AMI, HDB3, 2B1Q. Привести временные диаграммы сигналов. Рассчитать частоту Найквиста сигнала для каждого случая, если скорость передачи двоичных символов входной последовательности равна V=1Мбит/с. Укажите наиболее оптимальный код с точки зрения требуемой ширины полосы пропускания канала. Укажите известные Вам области применения этих кодов. На вход декодера сверточного кода с заданной решетчатой структурой поступила двоичная последовательность 10 01 01 00 11 01 11 00 11 01 11 01… Определить длину кодового ограничения и скорость сверточного кода. Декодировать принятую последовательность по алгоритму Витерби, приняв глубину декодирования равной 6, если не происходит более раннего слияния путей. Указать выжившие пути на каждом уровне решетки. При условии равных метрик, выбирать путь с наименьшей накопленной метрикой на предыдущем уровне решетки. Записать выходную последовательность. 2 3 0 1 4 00 00 00 00                11 11 11 11 11   11 00       01 00    01 01 10 10  10      10 10      01 01 Вечерний факультет, специальность 2009, 5 курс, дисциплина "Передача дискретных сообщений". Билет 20 Группа: ФИО студента: G1=(01) G2=(10) G3=(11) G4=(11) Нарисуйте структурную схему кодера и укажите, как меняется состояние схемы на каждом такте при подаче на вход информационной последовательности 1010. Запишите выходную последовательность. Укажите, чему равны длина кодового ограничения и скорость кода. Запишите образующие полиномы для данного кода. Поясните, является ли данный код разделимым. Устройство защиты от ошибок на базе системы с РОС с рабочим обратным каналом использует циклический код с вероятностью необнаруженной ошибки Рно=10-6 и вероятностью обнаружения ошибки Роо=10-2. Алгоритм работы – непрерывная передача с блокировкой приемника. Емкость буфера передачи h=4 сообщения. Нарисуйте временные диаграммы работы системы в режиме нормальной работы, переспроса (ошибка обнаружена и исправлена), выпадения и вставки сообщений. В случае использования ДСК без памяти в обоих направлениях с =10-3 рассчитайте вероятность выпадения Рвып и вероятность вставки Рвст сообщения. Вечерний факультет, специальность 2009, 5 курс, дисциплина "Передача дискретных сообщений". Билет 21 Группа: ФИО студента: Построить код Хемминга с длиной кодового слова n=15. Запишите формулу, выражающую связь между числом проверочных символов и длиной кодового слова для кодов Хемминга. Запишите формулы для определения значений проверочных символов кода. Исправьте ошибку в двоичной последовательности, закодированной кодом Хемминга с n=15 101 110 010 001 000. Циклический код (7,4) с образующим полиномом g(x)=x3+x2+1 исправляет все одиночные ошибки. Принята последовательность 1010101. Запишите синдром ошибки в принятой последовательности и типовой синдром, используемый декодером. Найдите вектор ошибки и кодовое слово на выходе декодера. Найдите два вектора ошибок, которые приведут к ошибочному декодированию. Вечерний факультет, специальность 2009, 5 курс, дисциплина "Передача дискретных сообщений". Билет 22 Группа: ФИО студента: Устройство защиты от ошибок на базе системы с РОС со специальным обратным каналом использует циклический код с вероятностью необнаруженной ошибки Рно=10-5 и вероятностью обнаружения ошибки Роо=10-2. Алгоритм работы – система с ожиданием сигналов решения и нумерацией сообщений в прямом канале. Длина сигнала обратной связи m=4 дв.симв. Нарисуйте временные диаграммы работы системы в режиме правильной работы (ошибка обнаружена и исправлена), выпадения и вставки сообщений. В случае использования ДСК без памяти в обоих направлениях с =10-2 рассчитайте вероятность выпадения Рвып и вероятность вставки Рвст сообщения. Декодер циклического кода (7,4) с образующим полиномом g(x)=x3+x+1 используется для исправления одиночных ошибок. На вход декодера поступает последовательность 0111110. Нарисуйте структурную схему декодера и укажите, как меняется состояние схемы на каждом такте до момента исправления ошибки. Запишите синдром ошибки в принятой последовательности и типовой синдром, используемый декодером. Вечерний факультет, специальность 2009, 5 курс, дисциплина "Передача дискретных сообщений". Билет 23 Группа: ФИО студента: Декодер циклического кода (7,4) с образующим полиномом g(x)=x3+x2+1 используется для исправления одиночных ошибок. На вход декодера поступает последовательность 1000001. Нарисуйте структурную схему декодера и укажите, как меняется состояние схемы на каждом такте до момента исправления ошибки. Запишите синдром ошибки в принятой последовательности и типовой синдром, используемый декодером. Запишите кодовое слово на выходе декодера. На вход декодера сверточного кода с заданной решетчатой структурой поступила двоичная последовательность 01 00 01 01 11 11 01 11 11 01 11 11… Определить длину кодового ограничения и скорость сверточного кода. Декодировать принятую последовательность по алгоритму Витерби, приняв глубину декодирования равной 6, если не происходит более раннего слияния путей. Указать выжившие пути на каждом уровне решетки. При условии равных метрик, выбирать путь с наименьшей накопленной метрикой на предыдущем уровне решетки. Записать выходную последовательность. 2 3 0 1 4 00 00 00 00                11 11 11 11 11   11 00       01 00    01 01 10 10  10      10 10      01 01 Вечерний факультет, специальность 2009, 5 курс, дисциплина "Передача дискретных сообщений". Билет 24 Группа: ФИО студента: Д 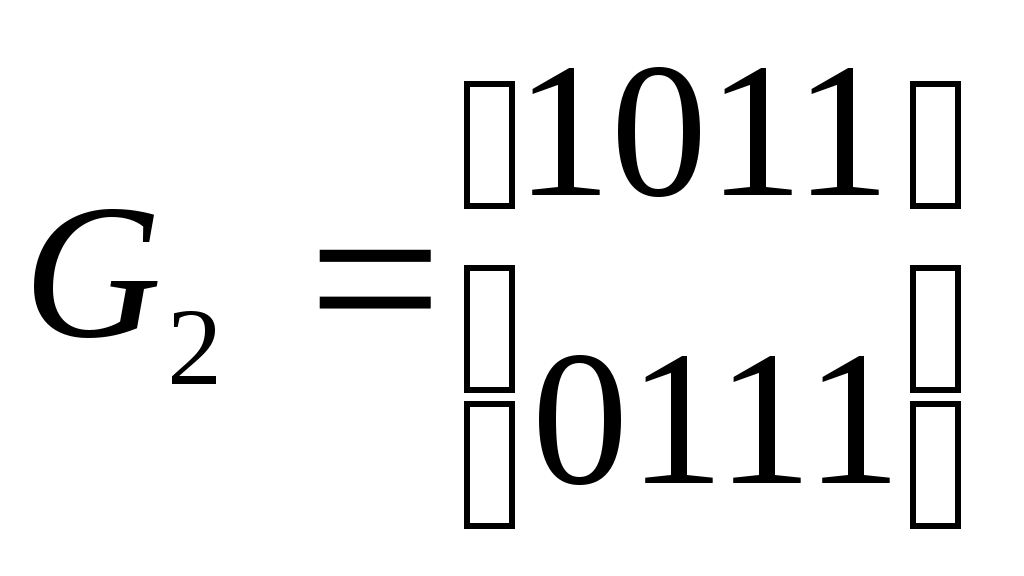 ва линейных кода (4, 2) заданы образующими матрицами 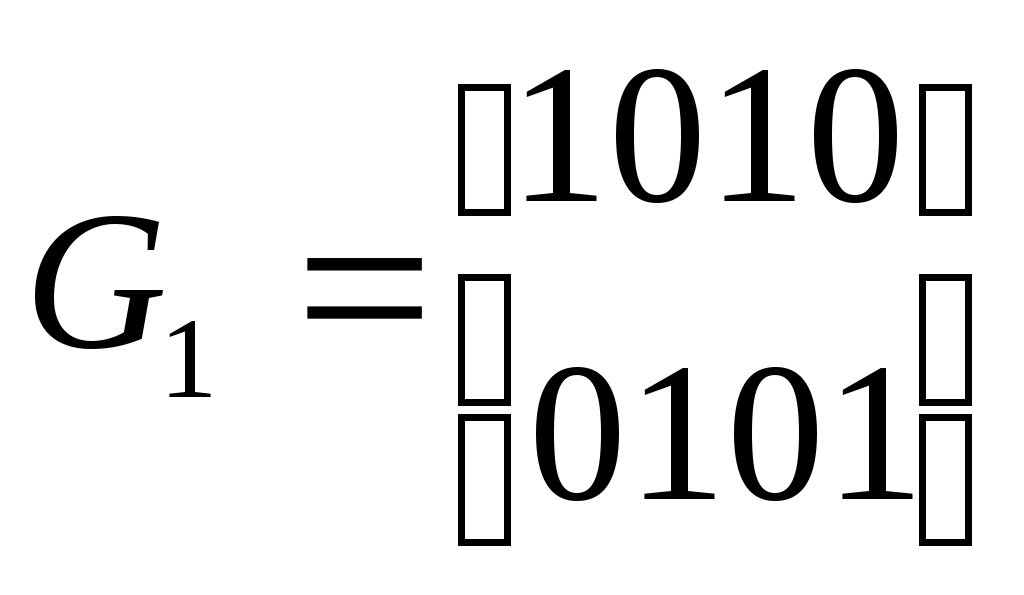 Найти кодовое расстояние для каждого из заданных кодов. Определить вес гарантированно обнаруживаемых и исправляемых ошибок для каждого из кодов. Найти вероятность необнаруженной ошибки при применении этих кодов в ДСК без памяти с вероятностью ошибки =0.1 . Запишите правила формирования кодовых слов для заданных кодов. Построить код Хемминга с длиной кодового слова n=15. Запишите формулу, выражающую связь между числом проверочных символов и длиной кодового слова для кодов Хемминга. Запишите формулы для определения значений проверочных символов кода. Исправьте ошибку в двоичной последовательности, закодированной кодом Хемминга с n=15 110 010 101 001 100. |
