Билеты. Билеты-ПДС. Передача дискретных сообщений
 Скачать 175.5 Kb. Скачать 175.5 Kb.
|
|
Вечерний факультет, специальность 2009, 5 курс, дисциплина "Передача дискретных сообщений". Билет 10 Группа: ФИО студента: Закодируйте двухбуквенный алфавит источника кодом Хаффмана, используя трехсимвольные блоки. Вероятность появления букв на выходе источника составляет P(Z1)=0.8 P(Z2)=0.2 .Определите среднюю длину кодового слова, энтропию алфавита источника и избыточность (бит / буква). Запишите двоичную последовательность на выходе кодера источника при появлении на выходе источника сообщения Z2Z2Z1Z2Z1Z1Z1Z1Z1 . Внесите ошибку в первый бит кодовой последовательности. Запишите сообщение, которое появится на выходе декодера источника. Сколько букв в сообщении источника принято неправильно? 2. Модем использует ДОФМ со следующими кодировками линейного сигнала
Нарисуйте диаграмму сигналов на фазовой плоскости. Нарисуйте временную диаграмму сигнала на выходе модема, если на вход подана двоичная последовательность 1 0 1 1 0 0 0 1 0 1 0 0 со скоростью 4800 бит/с. Чему равна скорость модуляции линейного сигнала и частота несущей? Какие методы разделения направлений передачи и приема может использовать такой модем при работе по 2-проводной линии? Вечерний факультет, специальность 2009, 5 курс, дисциплина "Передача дискретных сообщений". Билет 11 Группа: ФИО студента: Заданную двоичную последовательность 1 0 1 0 0 0 0 0 0 0 0 0 1 0 1 1 0 0 0 1 1 закодировать манчестерским кодом, AMI, HDB3, 2B1Q. Привести временные диаграммы сигналов. Рассчитать частоту Найквиста сигнала для каждого случая, если скорость передачи двоичных символов входной последовательности равна V=100 Кбит/с. Укажите наиболее оптимальный код с точки зрения необходимой ширины полосы пропускания канала. Укажите известные Вам области применения этих кодов. 2 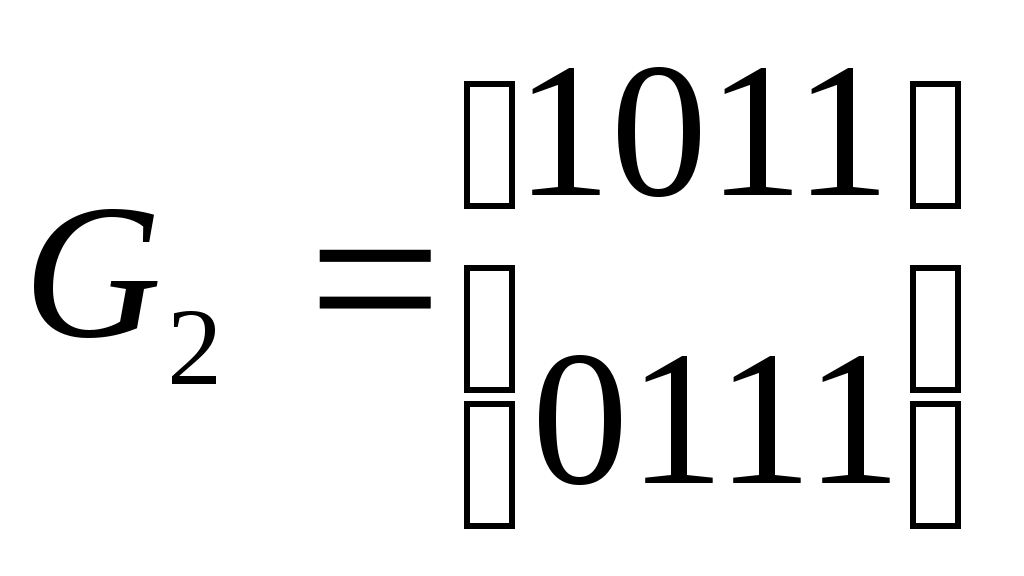 . Два линейных кода (4, 2) заданы образующими матрицами 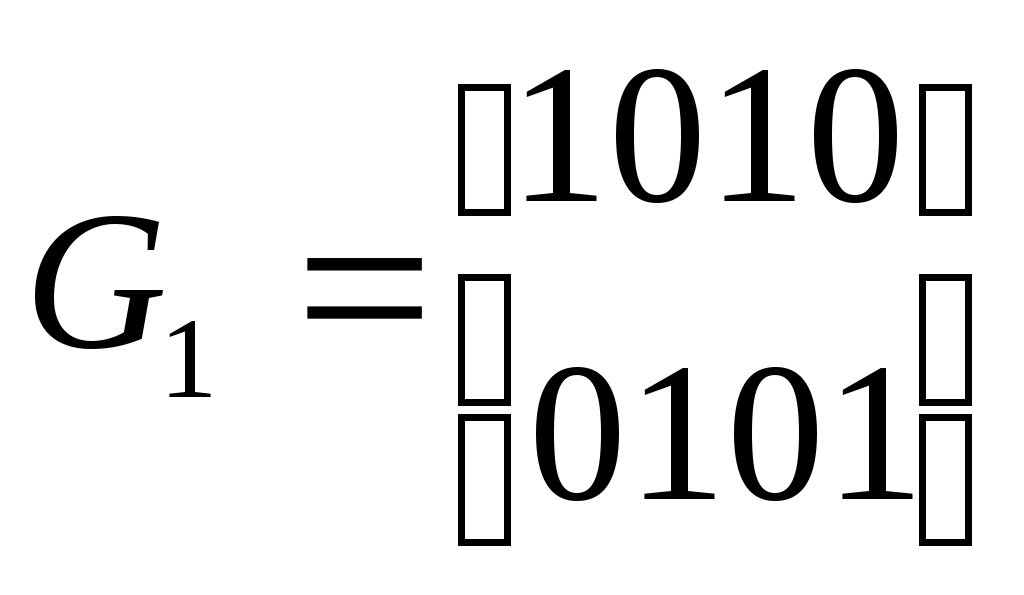 Найти кодовое расстояние для каждого из заданных кодов. Определить вес гарантированно обнаруживаемых и исправляемых ошибок для каждого из кодов. Найти вероятность необнаруженной ошибки при применении этих кодов в ДСК без памяти с вероятностью ошибки =0.01 . Запишите правила формирования кодовых слов для заданных кодов. Вечерний факультет, специальность 2009, 5 курс, дисциплина "Передача дискретных сообщений". Билет 12 Группа: ФИО студента: Закодируйте двухбуквенный алфавит источника кодом Шеннона-Фано, используя трехсимвольные блоки. Вероятность появления букв на выходе источника составляет P(Z1)=0.3 P(Z2)=0.7 .Определите среднюю длину кодового слова, энтропию алфавита источника и избыточность (бит / буква). Запишите двоичную последовательность на выходе кодера источника при появлении на выходе источника сообщения Z2Z2Z1Z2Z2Z1Z1Z2 . Внесите ошибку во второй бит кодовой последовательности. Запишите сообщение, которое появится на выходе декодера источника. Сколько букв в сообщении источника принято неправильно? 2. Модем использует ДОФМ со следующими кодировками линейного сигнала
Нарисуйте диаграмму сигналов на фазовой плоскости. Нарисуйте временную диаграмму сигнала на выходе модема, если на вход подана двоичная последовательность 1 0 1 1 0 0 0 1 0 1 со скоростью 1200 бит/с. Чему равна скорость модуляции линейного сигнала и частота несущей? Какой метод разделения направлений передачи и приема использует модем при работе по 2-проводной линии? Вечерний факультет, специальность 2009, 5 курс, дисциплина "Передача дискретных сообщений". Билет 13 Группа: ФИО студента: Для циклического (n, k) кода с образующим полиномом g(x) Построить образующую матрицу. Привести образующую матрицу к каноническому виду. Определить вес гарантированно обнаруживаемых и исправляемых кодом ошибок. Определить долю обнаруживаемых кодом ошибок в общем числе возможных ошибок. Найти синдром, соответствующий вектору ошибки e . Найти вектор ошибки весом t , имеющий такой же синдром. n=9, k=3, g(x)=x6+x3+1, e=000100000, t=4 Устройство защиты от ошибок на базе системы с РОС со специальным обратным каналом использует циклический код с вероятностью необнаруженной ошибки Рно=10-6 и вероятностью обнаружения ошибки Роо=10-2. Алгоритм работы – непрерывная передача с блокировкой приемника и нумерацией сообщений в прямом канале. Емкость буфера передачи h=3 сообщения, длина сигнала обратной связи m=3 дв.симв. Нарисуйте временные диаграммы работы системы в режиме правильной работы (ошибка обнаружена и исправлена), выпадения и вставки сообщений. В случае использования ДСК без памяти в обоих направлениях с =10-3 рассчитайте вероятность выпадения Рвып и вероятность вставки Рвст сообщения. Вечерний факультет, специальность 2009, 5 курс, дисциплина "Передача дискретных сообщений". Билет 14 Группа: ФИО студента: Для циклического (n, k) кода с образующим полиномом g(x) Построить образующую матрицу. Привести образующую матрицу к каноническому виду. Определить вес гарантированно обнаруживаемых и исправляемых кодом ошибок. Определить долю обнаруживаемых кодом ошибок в общем числе возможных ошибок. Найти синдром, соответствующий вектору ошибки e . Найти вектор ошибки весом t , имеющий такой же синдром. n=7, k=3, g(x)=x4+x3+x2+1, e=0010000, t=3 Заданную двоичную последовательность 1 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 закодировать кодом NRZ, манчестерским кодом, кодом AMI, HDB3, 2B1Q. Привести временные диаграммы сигналов. Рассчитать частоту Найквиста сигнала для каждого случая, если скорость передачи двоичных символов входной последовательности равна V=10 Кбит/с. Укажите наиболее оптимальный код с точки зрения ширины энергетического спектра сигнала. Обоснуйте ответ. Укажите известные Вам области применения этих кодов. Вечерний факультет, специальность 2009, 5 курс, дисциплина "Передача дискретных сообщений". Билет 15 Группа: ФИО студента: На вход декодера сверточного кода с заданной решетчатой структурой поступила двоичная последовательность 10 01 01 01 00 01 00 01 00 01… Определить длину кодового ограничения и скорость сверточного кода. Декодировать принятую последовательность по алгоритму Витерби, приняв глубину декодирования равной 6, если не происходит более раннего слияния путей. Указать выжившие пути на каждом уровне решетки. При условии равных метрик, выбирать путь с наименьшей накопленной метрикой на предыдущем уровне решетки. Записать выходную последовательность. 0 2 3 1 4 00 00 00 00                11 11 11 11 11   11 00       01 00    01 01 10 10  10      10 10    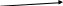  01 01 Заданную двоичную последовательность 0 0 1 1 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 закодировать кодом NRZ, квазитроичным кодом, HDB3, 2B1Q. Привести временные диаграммы сигналов. Рассчитать частоту Найквиста сигнала для каждого случая, если скорость передачи двоичных символов входной последовательности равна V=8 Кбит/с. Рассчитать необходимую ширину полосы пропускания канала для каждого случая при тех же условиях. Укажите известные Вам области применения этих кодов. Вечерний факультет, специальность 2009, 5 курс, дисциплина "Передача дискретных сообщений". Билет 16 Группа: ФИО студента: Для циклического (n, k) кода с образующим полиномом g(x) Построить образующую матрицу. Привести образующую матрицу к каноническому виду. Указать, какими свойствами линейных кодов обладает заданный код. Определить вес гарантированно обнаруживаемых и исправляемых кодом ошибок. Определить долю обнаруживаемых кодом ошибок в общем числе возможных ошибок. Найти синдром, соответствующий вектору ошибки e . Найти вектор ошибки весом t , имеющий такой же синдром. n=7, k=3, g(x)=x4+x2+x+1, e=0000100, t=3 G1=(10) G2=(01) G3=(11) Нарисуйте структурную схему кодера и укажите, как меняется состояние схемы на каждом такте при подаче на вход информационной последовательности 1010. Запишите выходную последовательность. Укажите, чему равны длина кодового ограничения и скорость кода. Запишите образующие полиномы для данного кода. Поясните, является ли данный код разделимым. Вечерний факультет, специальность 2009, 5 курс, дисциплина "Передача дискретных сообщений". Билет 17 Группа: ФИО студента: Нарисуйте структурную схему кодера циклического кода (7,3) с образующим полиномом g(x)=x4+x3+x2+1. Укажите, как меняется состояние схемы на каждом такте при подаче на вход информационной последовательности 011. Проверьте правильность полученных проверочных символов, сформировав кодовую комбинацию разделимого циклического кода для заданной информационной последовательности и заданного образующего полинома. Определите кодовое расстояние заданного кода. О 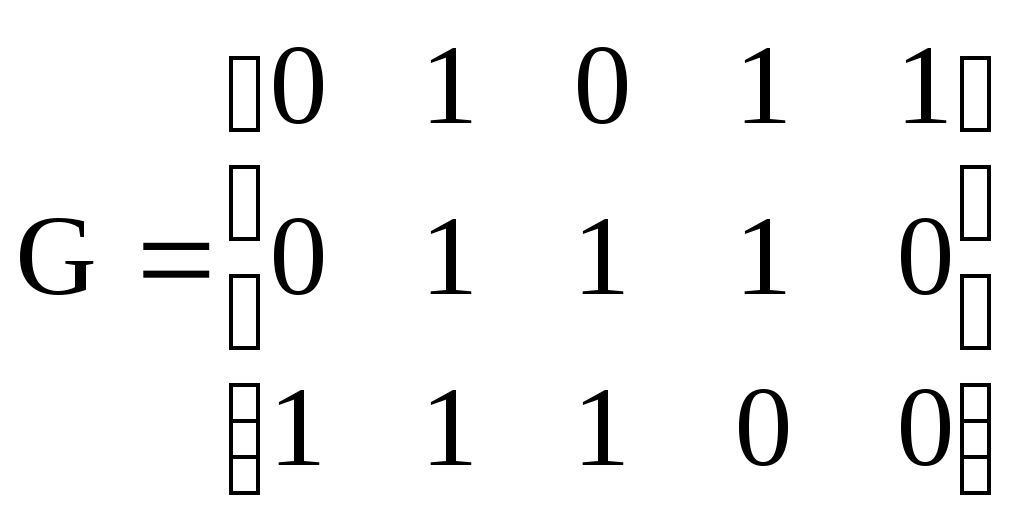 бразующая матрица линейного кода имеет вид Определите параметры кода (n,k) и запишите систему уравнений, задающих символы кода Vi. Запишите проверочную матрицу данного кода. Рассчитайте скорость кода R и избыточность кода W. Найдите вероятность необнаруженной ошибки при применении этого кода в ДСК без памяти с вероятностью ошибки в двоичном символе =0.01 . Вечерний факультет, специальность 2009, 5 курс, дисциплина "Передача дискретных сообщений". Билет 18 Группа: ФИО студента: Для циклического (n, k) кода с образующим полиномом g(x) Записать образующую матрицу. Привести образующую матрицу к каноническому виду. Определить вес гарантированно обнаруживаемых и исправляемых кодом ошибок. Укажите, какими свойствами линейных кодов обладает заданный код. Определить долю обнаруживаемых кодом ошибок в общем числе возможных ошибок. Найти синдром, соответствующий вектору ошибки e . Найти вектор ошибки весом t , имеющий такой же синдром. n=8, k=5, g(x)=x3+x2+x+1, e=00000010, t=3 Кодер сверточного кода задан системой векторов G1=(10) G2=(01) G3=(11) G4=(11) Нарисуйте структурную схему кодера и укажите, как меняется состояние схемы на каждом такте при подаче на вход информационной последовательности 1110. Запишите выходную последовательность. Укажите, чему равны длина кодового ограничения и скорость кода. Запишите образующие полиномы для данного кода. Поясните, является ли данный код разделимым. |
