РГР оп матану 3 вариант. Первое высшее техническое учебное заведение россии министерство науки и высшего образования российской федерации
 Скачать 99.56 Kb. Скачать 99.56 Kb.
|
|
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ  МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего образования «САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ» Кафедра высшей математики Расчётно-графическая работа №1 Вариант №3 Выполнил: студент гр. ГС-20-1 _____________ Бутасов Г.Д. (подпись) Проверил: доцент кафедры _____________ Брылевская Л.И. (подпись) Санкт-Петербург 2020 Задание №1 Написать уравнение такой окружности, чтобы ее диаметр оказался отрезок прямой x+ y= 4, заключенный между осями координат. Найдём точки пересечения с осями координат: при x = 0, y = 4 при y = 0, x = 4 Тогда точками пересечения прямой с осями являются точки А(4, 0) и В(0, 4), и выберем необходимый отрезок: 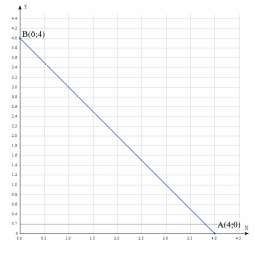 Из графика заметим, что отрезок АВ является гипотенузой прямоугольного треугольника АОВ. Тогда можем найти её длину через теорему Пифагора: 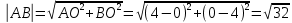 Далее найдём координаты центра окружности, диаметром которой является отрезок АВ, то есть найдём координаты середины отрезка: 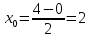 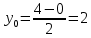 Напишем уравнение окружности: 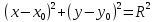 Где R – радиус, а x0 и y0 – координаты центра данной окружности. Тогда искомое уравнение будет выглядеть таким образом: 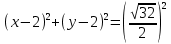 Построим получившуюся окружность: 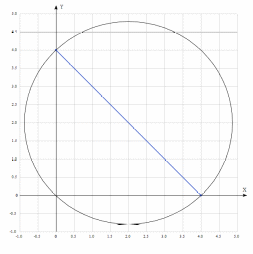 Задание №2 Привести к каноническому виду уравнение 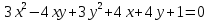 кривой второго порядка, выполнив последовательный поворот, а затем параллельный перенос координатных осей. Это уравнение имеет вид: 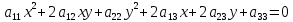 , ,где 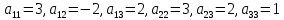 Вычислим определитель 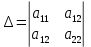 и подставим значения: 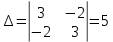 Так как определитель не равен нулю, то найдём центр канонической системы координат. Для этого решим систему уравнений: 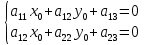 , , и подставив значения: 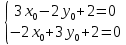 , , получим, что центром новой системы является точка О(-2,-2). Тем самым мы перешли к уравнению в системе координат O’X’Y’: 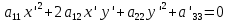 , ,где 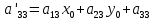 или или 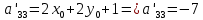 , ,тогда уравнение превратится в такое: 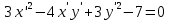 Теперь поворачиваем полученную систему координат на угол 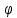 : :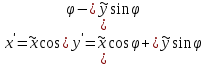 Находим 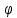 : :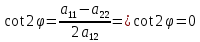 Тогда 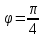 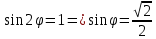 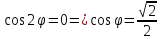 Подставим коэффициенты: 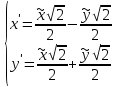 Уравнение будет таким: 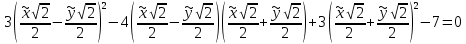 И после упрощения: 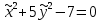 Данное уравнение является уравнением эллипса: 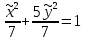 Построим получившийся эллипс: 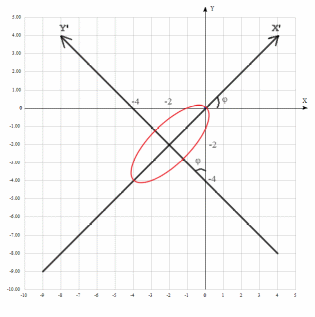 |
