РГЗ ФИЗИКа. РГЗ ФИЗИКА. Первое высшее техническое учебное заведение россии министерство науки и высшего образования российской федерации
 Скачать 336.65 Kb. Скачать 336.65 Kb.
|
|
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ  МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего образования «САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ» По дисциплине: Физика __________________ (наименование учебной дисциплины согласно учебному плану) РАСЧЕТНО-ГРАФИЧЕСКОЕ ЗАДАНИЕ ВАРИАНТ № 9 ВЫПОЛНИЛ: студент гр. ГК-18-2 _________ Киселева Д.Е. (шифр группы) (подпись) (Ф.И.О.) ДАТА: ____________ ПРОВЕРИЛ: доцент _________ Стоянова Т.В. (должность) (подпись) (Ф.И.О.) Санкт-Петербург 2019 ТЕОРЕТИЧЕСКИЕ ОСНОВЫ АТОМНОЙ И ЯДЕРНОЙ ФИЗИКИ №1 Явление, изучаемое в работе: квантование момента импульса в водородоподобном атоме. Определения и законы и соотношения, описывающие изучаемые процессы Наиболее вероятное расстояние электрона в состоянии n от ядра: 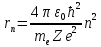 (1) (1)где me – масса электрона, Z – заряд ядра (атомный номер), n=1, 2, 3 – главное квантовое число. При n=1 и Z=1 это расстояние совпадает с радиусом первой боровской орбиты. Одновременное измерение модуля момента импульса и трёх его проекций на оси координат в квантовой механике невозможно. Модуль момента импульса определяется: 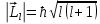 (2) (2)Число ℓ=0, 1, 2,…n-1.. называется орбитальным квантовым числом. Проекция момента импульса на любую ось (z) тоже может принимать лишь определенные значения 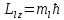 , (3) , (3)где mℓ=0, ±1, ±2, …, ±ℓ и называется магнитным квантовым числом. Такое название связано с тем, что оно определяет также проекцию магнитного момента, создаваемого движением электрона вокруг ядра: 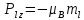 . (4) . (4)Модуль магнитного момента электрона 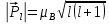 (5) (5)где 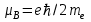 =0,927∙10-23 Дж/Тл - магнетон Бора. Гиромагнитное отношение для орбитальных магнитного и механического моментов =0,927∙10-23 Дж/Тл - магнетон Бора. Гиромагнитное отношение для орбитальных магнитного и механического моментов 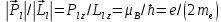 (6) (6)Электрон обладает также собственным механическим моментом импульса, равным 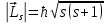 , (7) , (7)где s=1/2–спиновое квантовое число. Соответствующий ему магнитный момент также квантован 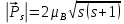 . (8) . (8)Проекции спинового момента импульса и магнитного момента на направление внешнего магнитного поля равны 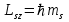 и и 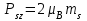 , (9) , (9)где ms – спиновое квантовое число, может принимать значения ±1/2. Гиромагнитное отношение для спиновых магнитного и механического моментов оказывается в два раза больше, чем для орбитальных моментов 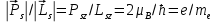 . (10) . (10)Орбитальный 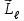 и спиновый и спиновый 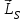 моменты импульса электрона складываются и дают полный момент импульса электрона моменты импульса электрона складываются и дают полный момент импульса электрона 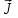 (рис.1). Он квантуется так же: (рис.1). Он квантуется так же: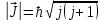 (11) (11)где 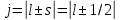 - внутреннее квантовое число. Проекция полного момента на направление внешнего магнитного поля - внутреннее квантовое число. Проекция полного момента на направление внешнего магнитного поля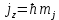 , (12) , (12)где mj может принимать 2j+1 значение от –j до j. Таким образом, для описания состояния электрона в атоме используют четыре квантовых числа: n, ℓ, mℓ и ms. или n, ℓ, j, mj. Из-за разных гиромагнитных отношений для спинового и орбитального моментов суммарный магнитный момент оказывается не параллельным суммарному механическому моменту. Поэтому вводится специальный коэффициент g–фактор Ланде, который есть не что иное, как коэффициент пропорциональности между 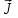 и и 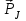 : :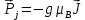 , (13) , (13)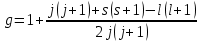 . (14) . (14)Порядок заполнения уровней в атоме определяется эмпирическими правилами Клечковского. Первое правило Клечковского: сначала будут заполняться уровни с наименьшей суммой квантовых чисел n+ℓ. Второе правило Клечковского: если два уровня имеют одинаковую сумму квантовых чисел n+ℓ, то первым будет заполняться энергетический уровень с меньшим значением n. Электроны подчиняются принципу Паули: каждый энергетический уровень может быть заселен не более чем двумя электронами с противоположными спинами. Вырожденные состояния электроны заселяют таким образом, чтобы спин 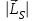 атома был максимален и, при этом по возможности максимальным было значение атома был максимален и, при этом по возможности максимальным было значение 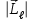 – правило Гунда. – правило Гунда. ЗАДАНИЯ ДЛЯ РАСЧЕТНО-ГРАФИЧЕСКОЙ РАБОТЫ Задача 1 1.1. Найдите наиболее вероятное расстояние электрона от ядра в состоянии n1. 1.2. Определите максимальное число электронов, находящихся в состояниях, описываемых данным главным квантовым числом n1. 1.3. Определите модуль орбитального момента импульса электрона при заданном n1; 1.4. Найдите все возможные проекции орбитального момента импульса электрона на направление внешнего магнитного поля, при заданном главном квантовом числе n1. Какое максимальное число проекций момента импульса на направление внешнего магнитного поля возможно в этом случае? 1.5. Найдите модуль магнитного момента электрона 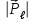 1.6. Определите все возможные проекции магнитного момента импульса электрона на направление внешнего магнитного поля 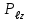 , при заданном главном квантовом числе n1. , при заданном главном квантовом числе n1.1.7. Чему равен максимально возможный, при заданном n1, полный момент импульса электрона 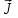 ? Определите для этого случая g– фактор Ланде ? Определите для этого случая g– фактор ЛандеТаблица 1. Исходные данные задач 1 и 2
РЕШЕНИЕ ЗАДАНИЯ 1 1.1. Наиболее вероятное расстояние электрона от ядра в состоянии c заданным n определяется по формуле:  Подставим заданные по условию варианта значения n1=1 и Z=47 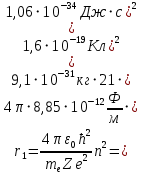 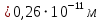 1.2. Максимальное число электронов, находящихся в состояниях, описываемых заданным главным квантовым числом n1=1: 1.3. Модуль орбитального момента импульса электрона определяется: Орбитальное квантовое число ℓ может принимать значения: 0,1,2…n-1. Так как n=1, то орбитальное квантовое число может иметь только одно значение, равное нулю. Тогда: Электрон на первом уровне находится в S – состоянии. 1.4. Проекция момента импульса на любую ось (z) тоже может принимать лишь значения: 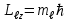 , ,где магнитное квантовое число может принимать значения mℓ=0, ±1, ±2, …, ±ℓ. При n=1, ℓ=0 следовательно mℓ=0 и проекция орбитального момента импульса электрона равна 0. В этом случае максимальное число проекций момента импульса будет: 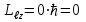 . .1.5. Модуль магнитного момента электрона 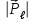 определяется: определяется:Так как магнитный момент зависит от орбитального квантового числа, а при заданных условиях ℓ=0, то и модуль магнитного момента также равен нулю. 1.6. Проекции магнитного момента импульса электрона на направление внешнего магнитного поля 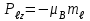 Так как проекции магнитного момента импульса электрона определяются магнитным квантовым числом, а оно принимает значение mℓ=0, то проекция магнитного момента импульса электрона также будет равна 0. 1.7. Модуль полного момента импульса электрона 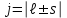 . Спиновое число для электрона может принимать два значения: . Спиновое число для электрона может принимать два значения: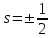 . При n1=1, ℓ=0 и . При n1=1, ℓ=0 и 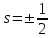 получим: получим: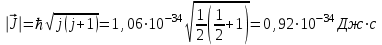 g– фактор Ланде определяется: 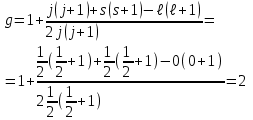 РЕЗУЛЬТАТ Наиболее вероятное расстояние электрона от ядра 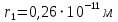 , , максимальное число электронов 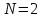 , , модуль орбитального момента импульса электрона 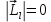 , , проекция момента импульса на любую ось (z) и модуль магнитного момента и его проекция тоже равны нулю, модуль полного момента импульса электрона 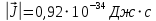 , ,g– фактор Ланде 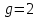 . . ТЕОРЕТИЧЕСКИЕ ОСНОВЫ АТОМНОЙ И ЯДЕРНОЙ ФИЗИКИ №2 Явление, изучаемое в работе: переход электрона с одной орбиты на другую в возбуждённом водородоподобном атоме . Определения и законы и соотношения, описывающие изучаемые процессы Фотон — элементарная частица, квант электромагнитного излучения. Это безмассовая частица, способная существовать только двигаясь со скоростью света. Энергия фотона — это энергия элементарной частицы (фотона), квант электромагнитного излучения (в узком смысле — света). Это безмассовая частица, способная существовать только двигаясь со скоростью света. 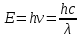  Один электрон-вольт равен энергии, которая необходима для переноса электрона в электростатическом поле между точками с разницей потенциалов в 1 В. Так как работа при переносе заряда q равна qU (где U — разность потенциалов), а заряд электрона составляет −1,6·10−19 Кл, то 1 эВ=1,6·10−19 Дж Серия Лаймана – спектральная серия в спектре атома водорода, которая образуется при переходах электронов с возбужденных энергетических уровней на первый в спектре излучения и с первого уровня на все вышележащие уровни при поглощении. Первый постулат Бора (постулат стационарных состояний): в атоме существуют стационарные (не изменяющиеся со временем) состояния, в которых он не излучает энергии. Второй постулат Бора (правило частот): при переходе электрона с одной стационарной орбиты на другую излучается (поглощается) один фотон с энергией 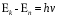 . .Закон Мозли: 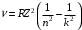 . .ЗАДАНИЯ ДЛЯ РАСЧЕТНО-ГРАФИЧЕСКОЙ РАБОТЫ Задание 2 2.1. Определите частоту перехода 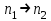 2.2. Какой длины волны освобождается /(поглощается) фотон. К какому диапазону длин волн электромагнитного спектра он относится. 2.3. Постройте графическую зависимость в соответствии с заданием варианта. РЕШЕНИЕ ЗАДАНИЯ 2 2.1. Определение частоты перехода 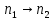 Так как по условию варианта задан атом скандия, то воспользуемся формулой Бальмера, для n1=1 и n2=2: 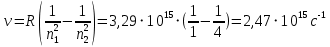 2.2. Определение длины волны фотона. 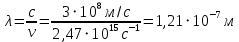 Длина волны соответствует коротковолновому ультрафиолетовому излучению. 2.3. Построение графических зависимостей, 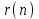 , ,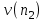 2.3.1. 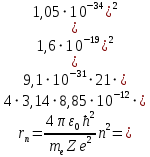 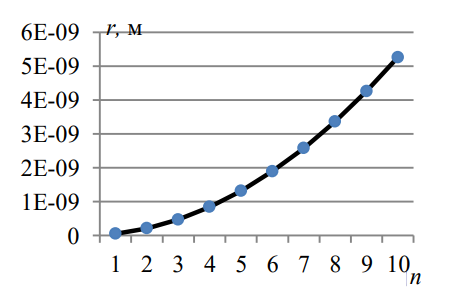 Рис. 1. Зависимость 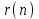 2.3.2. 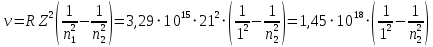 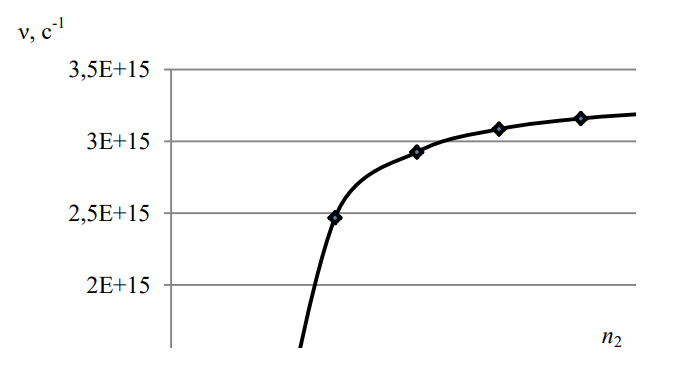 Рис. 2. Зависимость 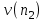 . .РЕЗУЛЬТАТ Частота 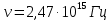 , ,Длина волны 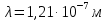 испущенного фотона, испущенного фотона,Были построены графические зависимости 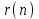 , ,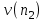 . .ЗАДАНИЯ ДЛЯ РАСЧЕТНО-ГРАФИЧЕСКОЙ РАБОТЫ Задание 3 Для элемента 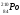 определите: определите:3.1. Число протонов в ядре; 3.2. Число нейтронов в ядре; 3.3. Найдите радиус ядра этого элемента. 3.4. Вычислите энергию связи нуклонов в ядре. 3.5. Определите удельную энергию связи в ядре. Исходные данные: Исходный элемент – полоний 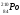 . Массовое число: A= 210, порядковый номер в таблице Менделеева: Z= 84. . Массовое число: A= 210, порядковый номер в таблице Менделеева: Z= 84. 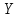 -элемент, образовавшийся в результате реакции – свинец -элемент, образовавшийся в результате реакции – свинец 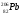 . Его массовое число: А – ΔА = 206, порядковый номер в таблице Менделеева: Z – ΔZ= 82. . Его массовое число: А – ΔА = 206, порядковый номер в таблице Менделеева: Z – ΔZ= 82. Теоретически возможна реакция: 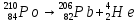 . .РЕШЕНИЕ ЗАДАНИЯ 3 3.1. Число протонов в исходном ядре: P= Z= 84 3.2. Число нейтронов в исходном ядре: N= A – Z= 210 – 84 = 126 3.3. Радиус ядра элемента зависит от массового числа: 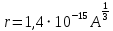 . .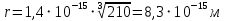 . .3.4. Энергии связи нуклонов в ядре определяется: 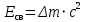 , где , где 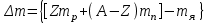 Тогда, при заданных условиях: 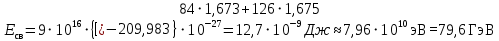 3.5. Определение удельной энергии связи ядра. 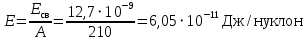 . .РЕЗУЛЬТАТ Найден радиус ядра полония 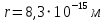 , , Вычислена энергия связи нуклонов в ядре 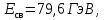 Определена удельная энергия связи в ядре 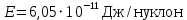 . .ЗАДАНИЯ ДЛЯ РАСЧЕТНО-ГРАФИЧЕСКОЙ РАБОТЫ Задание 4 4.1. Вычислите среднее время жизни радиоактивного элемента 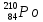 . .4.2. Сколько не распавшихся ядер осталось в 1 грамме исходного вещества осталось к моменту времени 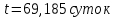 . .4.3. Вычислите активность исходного радиоактивного вещества. 4.4. Определите сколько 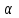 - и - и 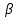 -распадов произошло при превращении элемента -распадов произошло при превращении элемента 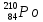 в элемент в элемент 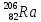 . .4.5. Определите с выделением или поглощением протекали эти реакции и величину энергии (выделившейся или поглощенной) РЕШЕНИЕ ЗАДАНИЯ 4 4.1. Вычисление времени жизни радиоактивного элемента 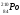 . Период полураспада . Период полураспада 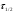 по условию – 138,37 суток. Тогда по условию – 138,37 суток. Тогда 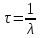 ; ;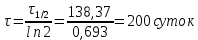 . .4.2. Определим, сколько не распавшихся ядер осталось в 1 грамме исходного вещества к моменту времени 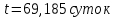 . .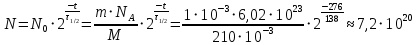 атомов атомов4.3. Вычисление активности исходного радиоактивного вещества: 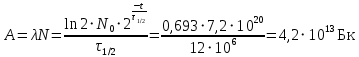 . .4.4. Определение количества 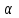 - и - и 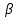 -распадов произошедших при превращении элемента -распадов произошедших при превращении элемента 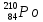 в элемент в элемент 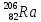 . .По условию А = 210 и А - 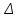 А = 206, следовательно массовое число уменьшилось на 4 единицы, Z= 84 и Z- А = 206, следовательно массовое число уменьшилось на 4 единицы, Z= 84 и Z-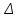 Z= 82 – зарядовое число уменьшилось на 2 единицы. Это возможно при одном альфа-распаде. Z= 82 – зарядовое число уменьшилось на 2 единицы. Это возможно при одном альфа-распаде.4.5. Определение величины энергии реакции (выделившейся или поглощенной) 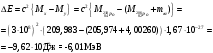 Реакция идёт с поглощением энергии. РЕЗУЛЬТАТ Найдено кол-во не распавшихся ядер в 1 грамме исходного вещества к моменту времени 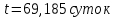 , , Вычислена активность исходного радиоактивного вещества, Определено сколько 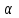 - и - и 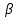 -распадов произошло при превращении элемента -распадов произошло при превращении элемента 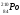 в элемент в элемент 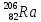 Определено, что реакция идёт с поглощением энергии. |
