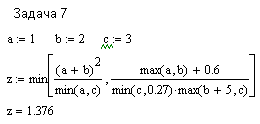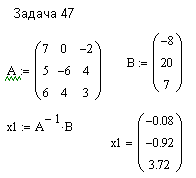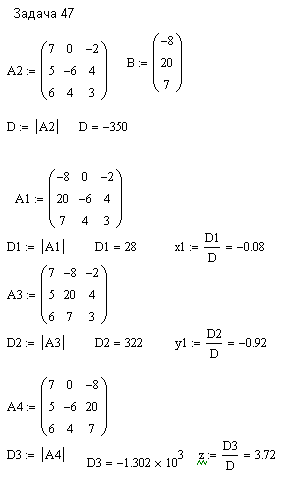Лабораторная работа с Delphi. Первое высшее техническое заведение россии министерство образования и науки российской федерации
 Скачать 1.02 Mb. Скачать 1.02 Mb.
|
|
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ ЗАВЕДЕНИЕ РОССИИ  МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего образования «САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ» Кафедра информатики и компьютерных технологий Лабораторная работа №4 По дисциплине Информационные технологии (наименование учебной дисциплины согласно учебному плану) Тема: Лабораторная работа с Delphi Вариант №1 Автор: студент гр. НГШ-20 Заболотский Д.В. (подпись) (Ф.И.О.) ОЦЕНКА: Дата: ПРОВЕРИЛ ассистент /Кочнева А.А. / (должность) (подпись) (Ф.И.О) Санкт-Петербург 2020 год ОглавлениеВведение 3 Линейно-вычислительный процесс 4 Разветвляющийся вычислительный процесс 7 Циклы суммирования 13 Цикл табулирования 16 Запись результата в файл 18 Одномерные массивы 21 Вектора 26 Матрицы 28 Построение графиков и поверхностей 31 Max,min 35 СЛАУ 36 Заключение. 38 ВведениеС помощью данной лабораторной работы можно понять, как решать различные задачи в Mathcad. Благодаря данной лабораторной работе можно рассмотреть, как реализуются и работают функции и команды в данном приложении. При реализации данной лабораторной работы было изучено много нового и необходимого для дальнейшего изучения приложения Mathcad. Также был получен опыт реализации серьезных задач. Информатика. Лабораторные работы Вариант 1 Задания к курсу “Информатика” I и II семестры1 Линейно-вычислительный процессЗадача 1.Вычислить площадь прямоугольного треугольника по формуле 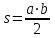 , где a, b – катеты треугольника. Получить ответ для a=0,83, b=1.2,298.2 , где a, b – катеты треугольника. Получить ответ для a=0,83, b=1.2,298.2Дано: a=0,83, b=1.2,298.2 Найти: s 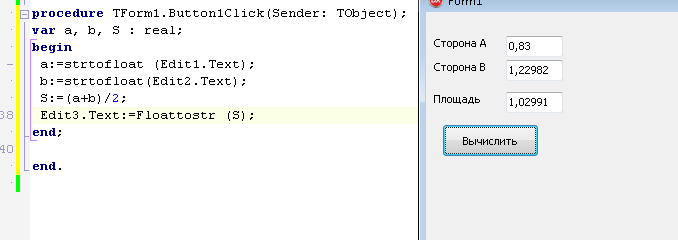 Рисунок 1- Задача 1 Y Начало  a, b  S=(a+b)/2  S  Конец Блок-схема 1- Задача 1 Задача 2. Задан круг радиуса r. В круг вписывается правильный 12-тиугольник, длина стороны которого a определяется по формуле 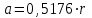 . Площадь правильного вписанного многоугольника вычисляется по формуле . Площадь правильного вписанного многоугольника вычисляется по формуле 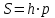 , где p – полупериметр, h – высота 12-тиугольника, связанная с радиусом соотношением , где p – полупериметр, h – высота 12-тиугольника, связанная с радиусом соотношением  . Вычислить площадь правильного вписанного 12-угольника и величину ее отношения к площади круга. Получить ответ для r=1,92 . Вычислить площадь правильного вписанного 12-угольника и величину ее отношения к площади круга. Получить ответ для r=1,92Дано: r=1,92 Найти:S  Р Начало исунок 2- Задача 2 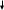 r 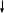 S=h*p l=S/(pi*r^2)  s, l  Конец Блок-схема 2 – Задача 2 Задача 3. Задан круг радиусом r. Вокруг круга описывается правильный шестидесятичетырехугольник, длина стороны a которого связана с радиусом вписанного круга формулой 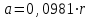 . .Найти периметр шестидесятичетырехугольника и разность между периметром и длиной заданной окружности. Получить ответ для r=0,59.3. Дано: r=0,59.3. Найти: Pи P-L 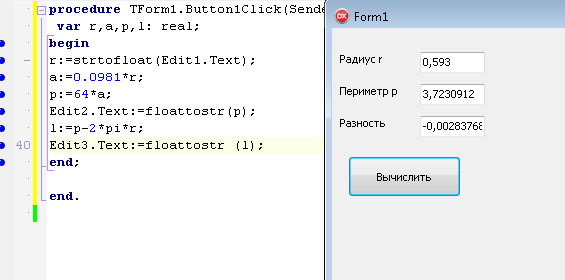 Р Начало исунок 3- Задача 3  r  a=0.0981*r p=64*a l=p-2*pi*r p, l   Конец Блок-схема 3 – Задача 3 Разветвляющийся вычислительный процессЗадача 4. Сравнить объемы куба со стороной a=1,2.77 и октаэдра со стороной a=2,12 и указать, который из них больше. Примечание. Объем куба вычисляется по формуле 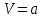 3, объем октаэдра – по формуле 3, объем октаэдра – по формуле 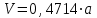 3 3Дано: ak=1,2.77, ao=2,12 Найти |Vk-Vo| и указать больший объем 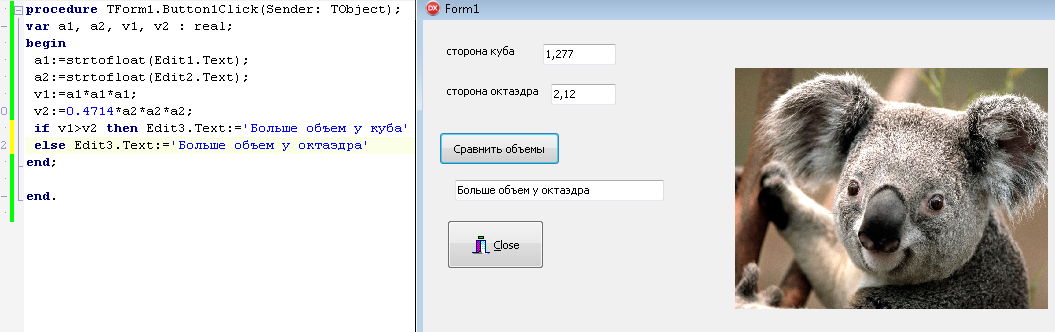 Р Начало исунок 8 – Задача 4  a1, a2  V1=a3 V2=0.4714*a3  V1>V2 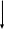 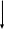 + - + -V1>V2 V1  Конец Блок-схема 4 – задача 4 Задача 5. Задан выпуклый четырехугольник ABCD со сторонами a, b, c, d. Сделать вывод о возможности вписать в него окружность при a=1,6, b=7,3, c=3,6, d=1,3. Указание: необходимым и достаточным условием возможности вписать окружность в четырехугольник является условие a+c=b+d Дано: a=1,6, b=7,3, c=3,6, d=1,3. Можно ли вписать окружность? 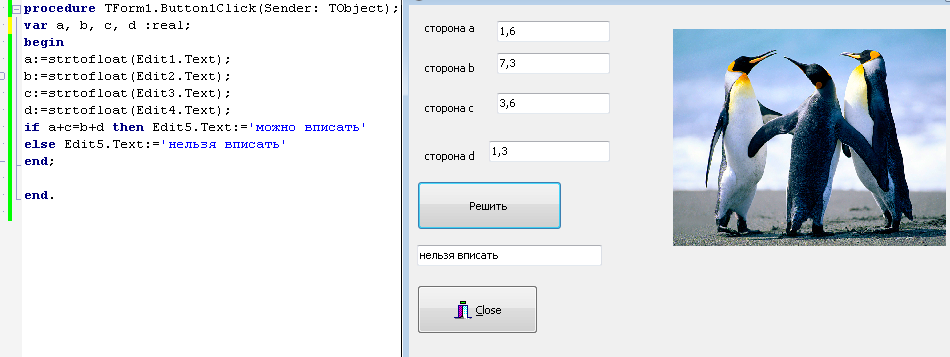 Рисунок 9 – Задача 5 Начало  a, b, c, d  a+c b+d  a+c=b+d   можно нельзя  Конец + - Блок-схема 5 – задача 5 Задача 6.В декартовых координатах задан круг .x2 + y2  16. Определить, попала ли точка с заданными координатами в круг. 16. Определить, попала ли точка с заданными координатами в круг.Получить ответ для x=1.0,4 y=2,72  Рисунок 10 – Задача 6 Начало  x,y  x2+y2  x2+y2≤16 + -   попала Не попала  Конец Блок-схема 6 – задание 6 Задача 45. Проверить справедливость утверждения 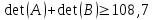 для матриц для матриц 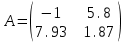 и и 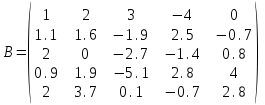  Рисунок 11 – Задача 45 Задача 46. Сделать вывод о наличии единственного решения системы линейных алгебраических уравнений  Указание: система имеет единственное решение, если ее определитель отличен от нуля.  Рисунок 12 – Задача 46 Radiobutton, checkboxЗадача 72. Задан правильный треугольник со стороной а. Радиус вписанной окружности определяется по формуле r =0,2887 a, радиус описанной - R=0,5774a. А) Создать программу, вычисляющую либо площадь вписанной, либо площадь описанной окружности. Ответ получить для случая а=3.86.  Рисунок 7 – Задача 72a Б) Создать программу, вычисляющую либо площадь вписанной, либо площадь описанной окружности, либо обе площади. Ответ получить для случая а=3.86. 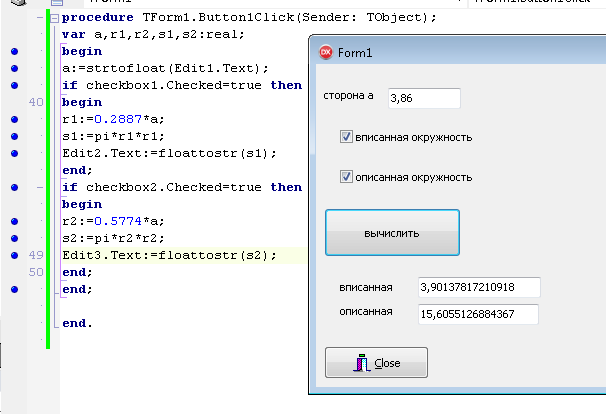 Рисунок 8 – Задача 72б Задача 73. Имеется прямоугольный параллелепипед со сторонами а, b, c (рис. 2). Создать программу, вычисляющую либо объем (V), либо площадь боковой поверхности (М), либо полную поверхность (S) параллелепипеда, либо все эти величины. Объем параллелепипеда определяется по формуле V=abc, площадь боковой поверхности М=2(ab+bc), площадь полной поверхности – по формуле S=2(ab+bc+ac). Ответ получить для случая а=3.86, b=1.7, c=0,56 . 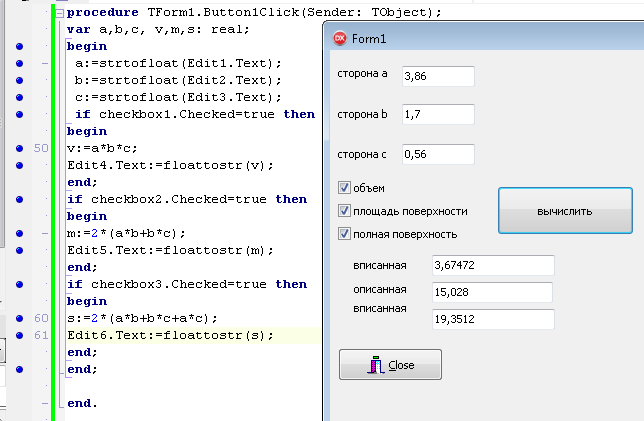 Рисунок 9 – Задача 73 Циклы суммированияЗадача 11. Вычислить суммы 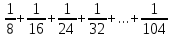  Р начало исунок 10 – Задача 11а  p=0 s=0 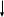  p=p+8 s=s+1/p  p<96 Да 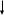 s нет 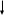 конец Блок-схема 7 – Задача 11а б)  ; ;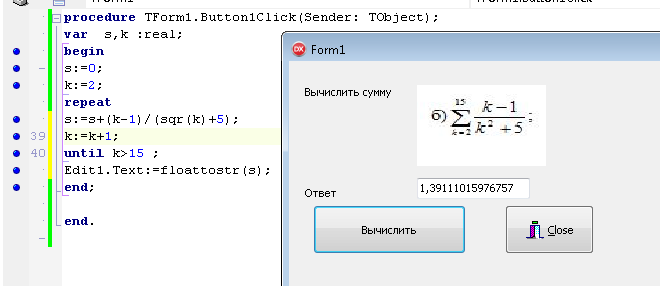 Рисунок 11 – Задача 11б начало  p=0 s=0  p=p+8 s=s+1/p  p<96   s  конец Да нет Блок-схема 8 – Задача 11б в)  при x=1.75 при x=1.75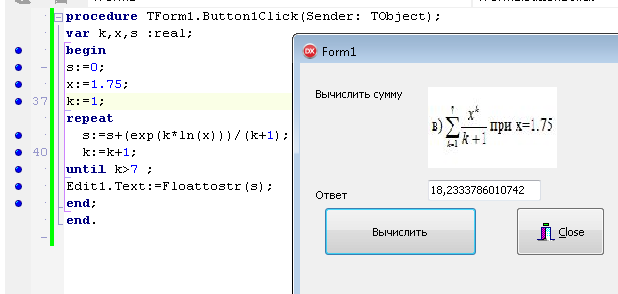 Рисунок 12 – Задача 11в начало  p=0 s=0  p=p+8 s=s+1/p  p<96   s  конец Да нет Блок-схема 8 – Задача 11в Цикл табулированияЗадача 8. Вычислить функцию y=2x+1.37 для следующих наборов значений аргумента: а) 1, 1.7, 2.4, 3.1 … 7.3 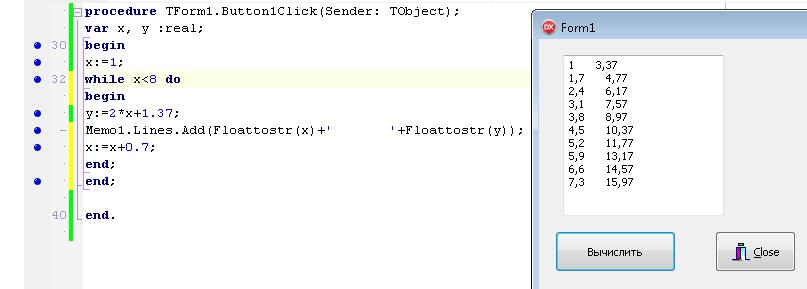 Р Начало исунок 13 – Задача 8а  x=1 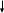 y=2*x+1,37   x, y 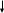 x=x+0,7  Да x<=7,3 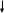 нет Конец Блок-схема 9 – Задача 8а б) 16, 4, 1, 1/4, 1/16, 1/64, 1/256 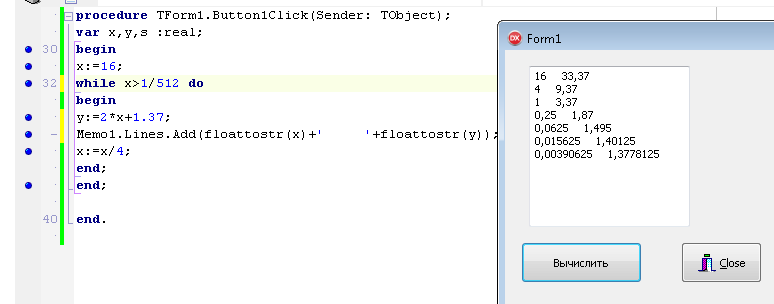 Рисунок 14 – Задача 8б Рисунок 14 – Задача 8бНачало  x=16  y=2*x+1,37  x, y  x=x/4  x<=1/512  Конец  Да нет Блок-схема 10 – Задача 8б Запись результата в файлЗадача 8. Вычислить функцию y=2x+1.37 для следующих наборов значений аргумента: в) 0.35, 0.3, 0.74, 1.3, 1.8, 2.05 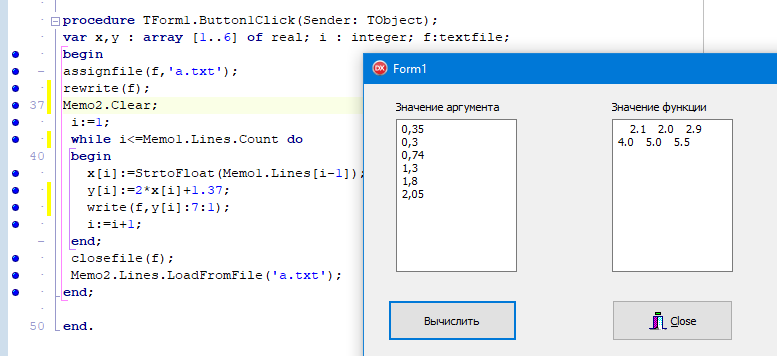 Р Начало  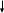  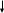 исунок 15 – Задача 8в исунок 15 – Задача 8в xi i=1 нет i<=6 Конец  Да 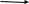 y=2*xi+1,37 ‘  xi, y  i=i+1 Блок-схема 11 – Задача 8в Задача 9. Вычислить значения функции 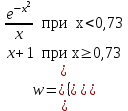 для следующих значений аргумента x: -0,5; -0,4; -0,3;…1.1. для следующих значений аргумента x: -0,5; -0,4; -0,3;…1.1. Р Начало  x=-0,5 исунок 16 – Задача 9 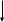  x<0,73 Да нет   w=  w=x+1  x, w  x=x+0,1  x<=1,1  Да нет Конец Блок-схема 12 – Задача 9 Задача 10. Вычислить значения функции  на промежутке [0.1, 2.5] в 10 точках. на промежутке [0.1, 2.5] в 10 точках.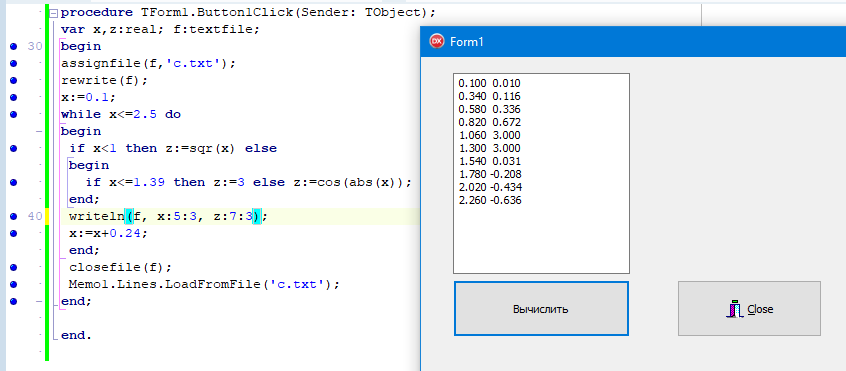 Р Начало  x=0,1   x<1 Да нет   исунок 17 – Задача 10 исунок 17 – Задача 10 нет z=x2 x<1,39   Да z=cos(|x|) z=3 x, z  x=x+0,24  x<=2,5  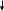 нет Конец Блок-схема 13 – Задача 10 Одномерные массивыЗадача 15. Задан вектор P={0.84, 6.5, -2, 5.17, 8.95, 9.4, -1.3}. Вычислить сумму его компонентов 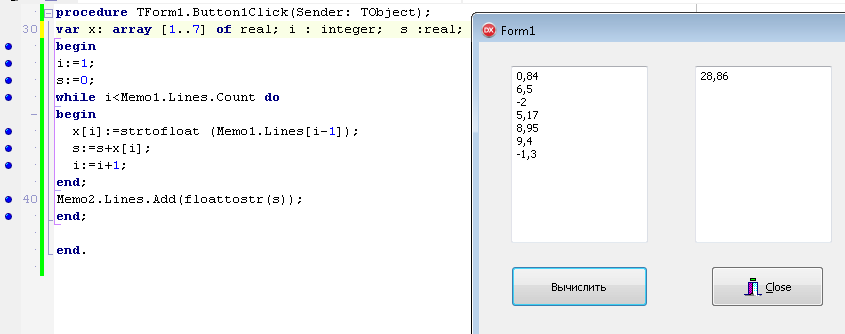 Рисунок 18 – Задача 15 Начало  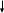 s:=s+xi  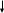 i<=7  Да нет xi  i=1 s=0 xi, y  Конец  i=i+1 Блок-схема 14 – Задача 15 Задача 16. Задан вектор C=(7.2, -3.3, 4.1, 5.7, 0.2, 1.7, -0.2, 8.4). Вычислить сумму его компонентов, удовлетворяющих условию 1  Р Начало исунок 19 – Задача 16  s:=s+ci  Да нет  s=0  ci    1 i:=i+1  Да i<=8 нет  x, w 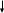 Конец Блок-схема 15 – Задача 16 Задача 18. Найти макcимальное значение элементов вектора E. Ответ получить для случая E=( 3.68, -7.98, -0.82, 4.73, 3.75, -2.38, -25.3, 7.98). 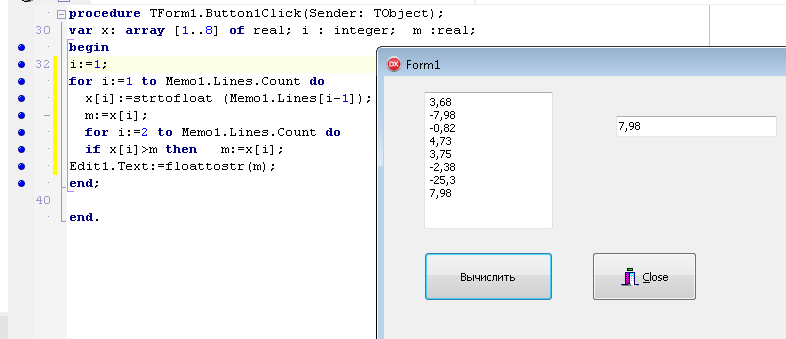 Рисунок 20 – Задача 18 начало  X  m=x  I=2  Xi>m  нет  да m=xi   i=i+1  i да нет  m  конец Блок-схема 16 – Задача 18 Задача 21. Подсчитать количество отрицательных элементов вектора. Ответ получить для случая E=(3.68, -7.98, -3.82, 4.73, 13.75, -2.38, -5.3, 7.98). 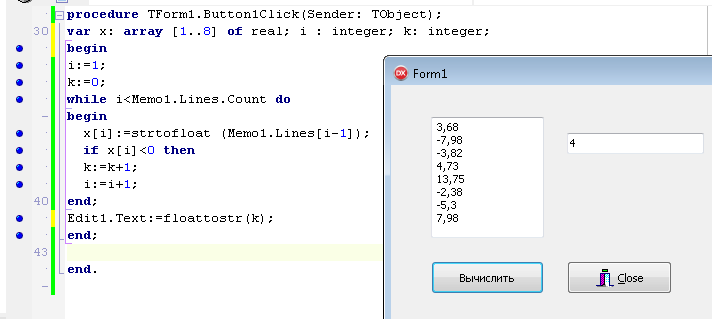 Рисунок 21 – Задача 21 Начало  k:=k+1  k i:-i+1 i<=8  Конец Да нет Да нет   xi<0 xi k=0       г) 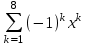 при x=3; при x=3;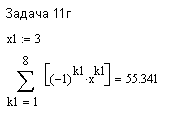 Рисунок 6 – Задача 11г Задача 63. Вычислить приближенное значение интеграла  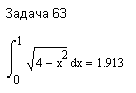 Рисунок 7 – Задача 63 ВектораЗадача 14. Вычислить вектор, получающийся при делении вектора F=(10.04, -6.3, -16.7, 28.4, -1.8) на число 4,5. 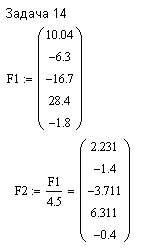 Рисунок 13 – Задача 14 Задача 15. Задан вектор 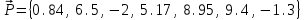 . Вычислить сумму его компонентов. . Вычислить сумму его компонентов. Рисунок 14 – Задача 15 Задача 23. Вычислить скалярное произведение векторов 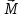 и и  . Ответ получить для случая N=(-1.7, 8.2, 0.3, 0.75, 0.16, 0.72) и M=(4.2, 0.95, 7.2, 4.6, -0.3, 2.6). . Ответ получить для случая N=(-1.7, 8.2, 0.3, 0.75, 0.16, 0.72) и M=(4.2, 0.95, 7.2, 4.6, -0.3, 2.6).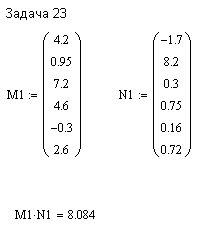 Рисунок 15 – Задача 23 МатрицыЗадача 35. Вычислить сумму элементов матрицы Y. Ответ получить для 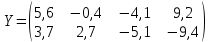 . .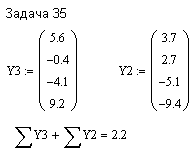 Рисунок 16 – Задача 35 Задача 38. Траспонировать матрицу 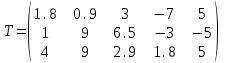 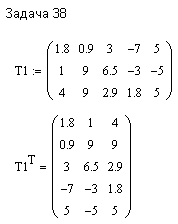 Рисунок 17 – Задача 38 Задача 39. Вычислить матрицу, являющуюся матрицей, умноженной на число 0.5. Ответ получить для матрицы 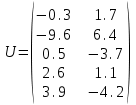  Рисунок 18 – Задача 39 Задача 40. Вычислить матрицу, являющуюся произведением двух матриц. Ответ получить для 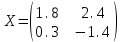 и и 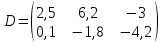 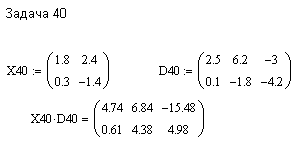 Рисунок 19 – Задача 40 Задача 42. Вычислить матрицу, являющуюся матрицей V в третьей степени. Ответ получить для 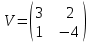 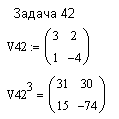 Рисунок 20 – Задача 42 Задача 44. Вычислить значение матричного выражения 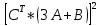 при при 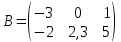 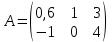 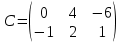 |

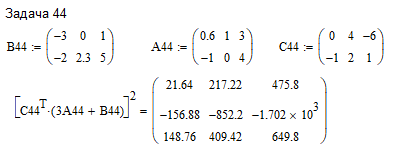
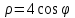 в полярной системе координат на промежутке φ[0,2π].
в полярной системе координат на промежутке φ[0,2π].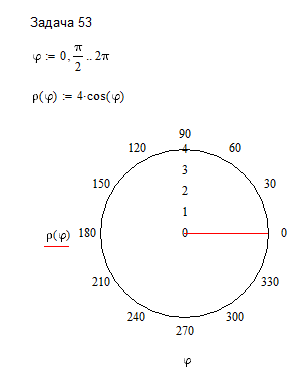
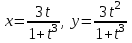 при изменении t на промежутке t[-0.5, 4.5].
при изменении t на промежутке t[-0.5, 4.5].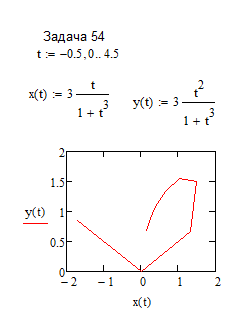
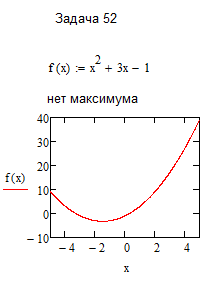
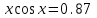 на промежутке x [-3, 4].
на промежутке x [-3, 4].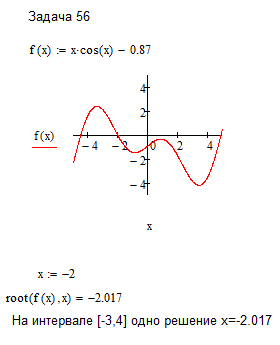
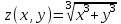 для диапазонов изменения переменных x[1, 4] и y[0, 5].
для диапазонов изменения переменных x[1, 4] и y[0, 5].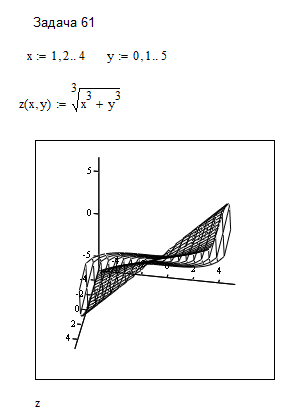
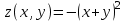 и
и 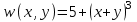 при х[-5, 5] и y[-4, 8].
при х[-5, 5] и y[-4, 8].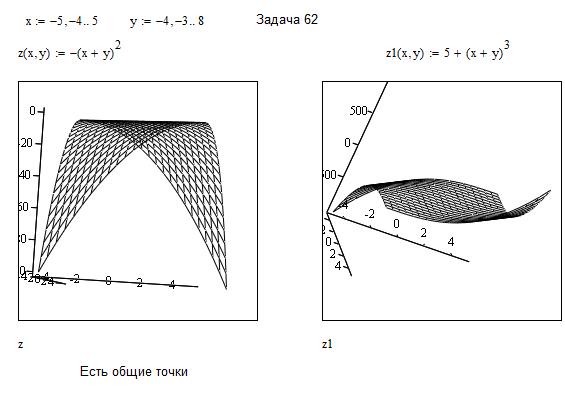
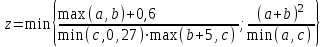 при a=1, b=2, c=4
при a=1, b=2, c=4