математикаа (1). Петеримова Венера Наильевна
 Скачать 78.13 Kb. Скачать 78.13 Kb.
|
Практическое задание
дисциплине
Пермь 2022 Вычислить предел 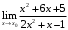 при приРешим 2 квадратных уравнения и разложим числитель и знаменатель на множители и сократим. 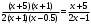 далее все просто подставляем значения далее все просто подставляем значенияа) х0=3 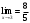 б)х0=-1  в)х0=∞  в этом случае неопределенность ∞/∞ решается убиранием из выражения членов без х. в этом случае неопределенность ∞/∞ решается убиранием из выражения членов без х.2. Найти производные функций. а)   по правилу по правилу 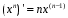 для любого n. для любого n.б)  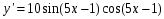 по правилу: по правилу:(sin(5·x-1)2)′=2·sin(5·x-1)2-1·sin(5·x-1)′=10·sin(5·x-1)·cos(5·x-1) в) 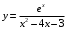  Было использовано правило дифференцирования дробей:  Составить уравнение касательной к графику функции 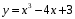 в точке х0=2. Уравнение касательной записывается так: y=f(x0)+f’(x0)*(x-x0) f(x0)=2^3-4*2+3=3 f’(x0)=3x02-4=8 Касательная: y=3+8(x-2)=8x-13 4. Вычислить неопределенный интеграл. а) 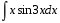 используем интегрирование по частям используем интегрирование по частям 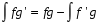 f=x, f’=1. g’=sin(3x) g= 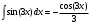 подставляем в формулу и получаем: подставляем в формулу и получаем: б) 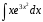 введем х под dx и решим интеграл с аргументом х2 введем х под dx и решим интеграл с аргументом х2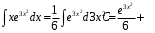 в) 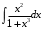 введем х2 под dx введем х2 под dx 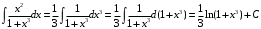 5. Вычислить площадь фигуры, ограниченной линиями y1=x2+4x+3 и y2=x+3. Построить график. 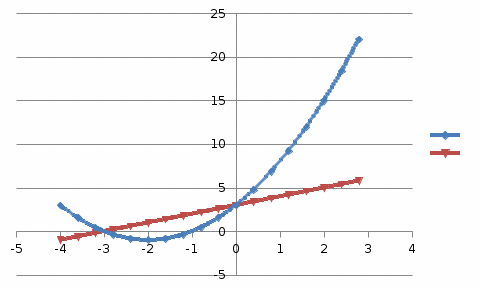 Точки пересечения функций х=-3 и х=0, график функции y2=x+3 лежит выше графика функции y1=x2+4x+3 тогда площадь фигуры выразится как определенный интеграл: 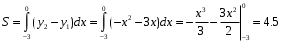 | ||||||||||||||||||||||||||||||||||||||||||||||||
