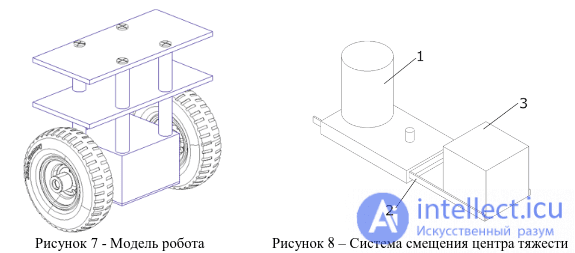
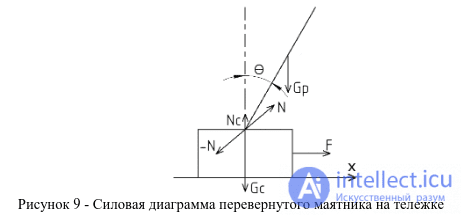
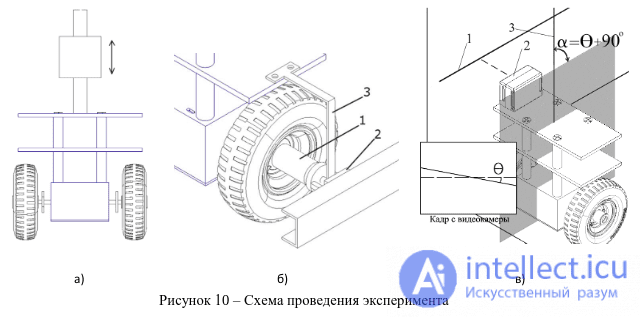
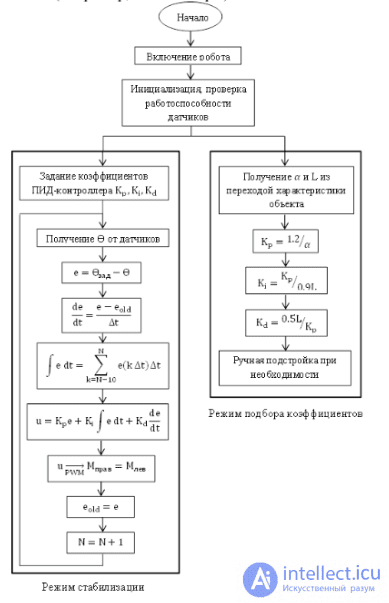
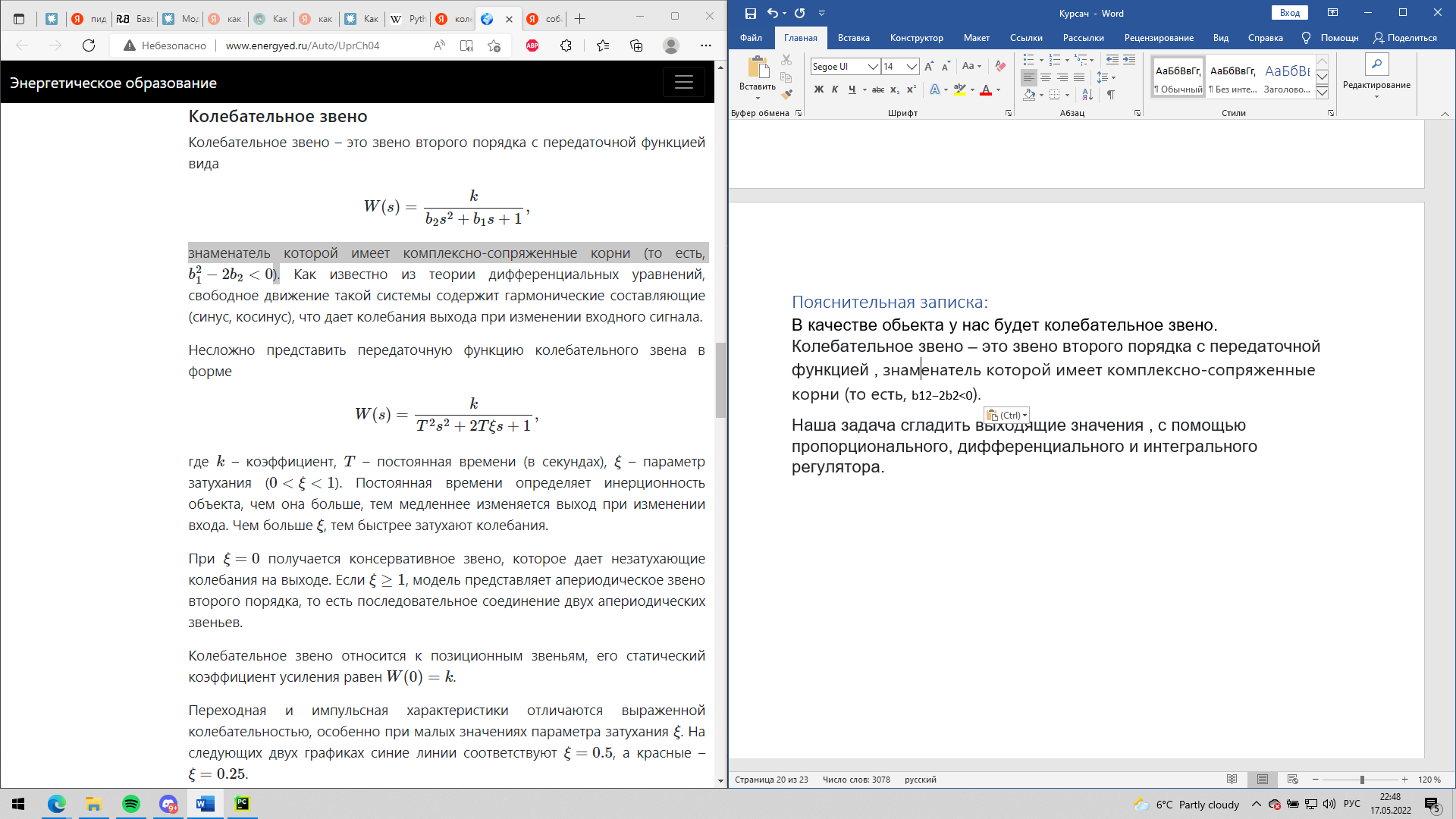
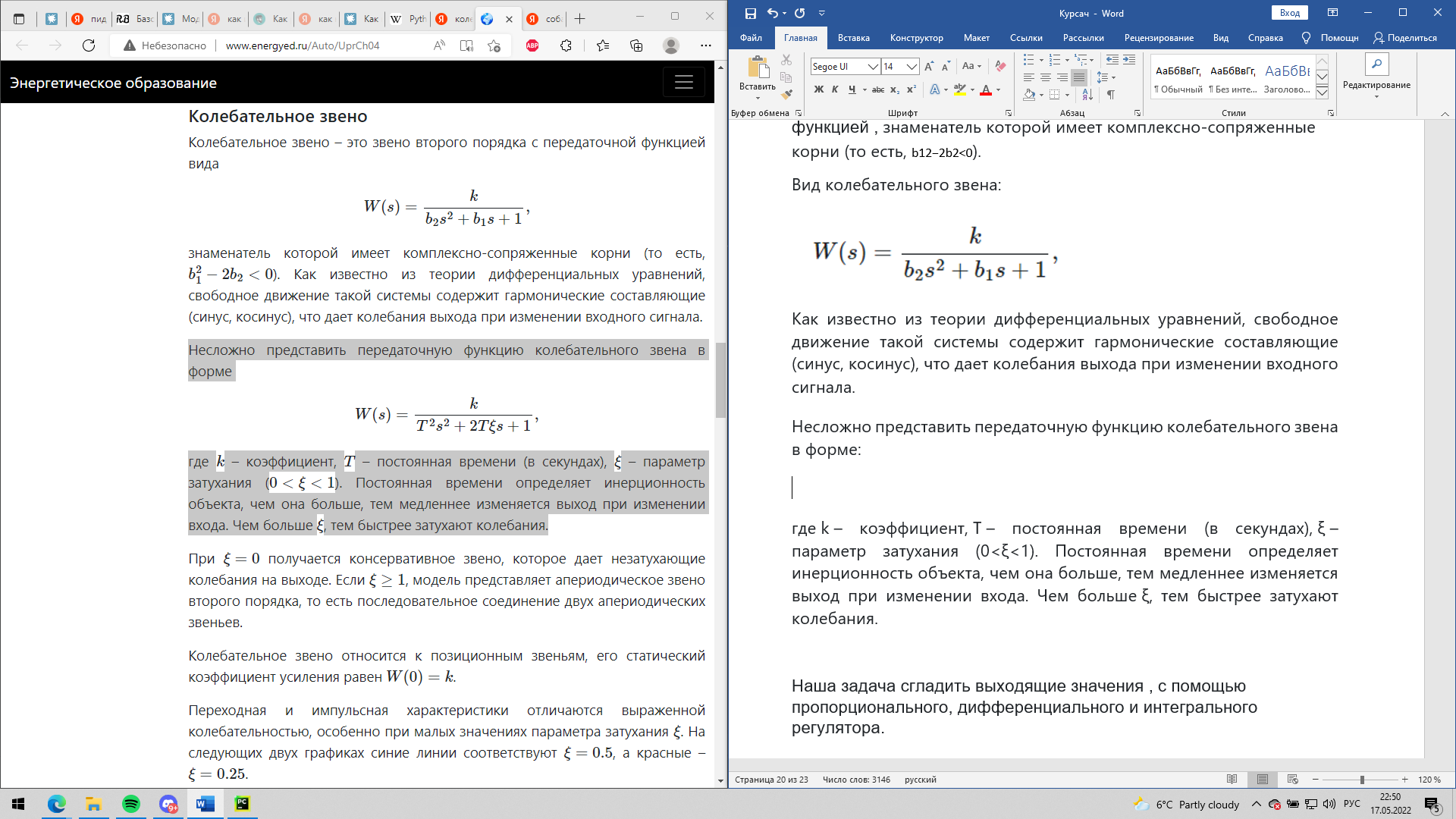
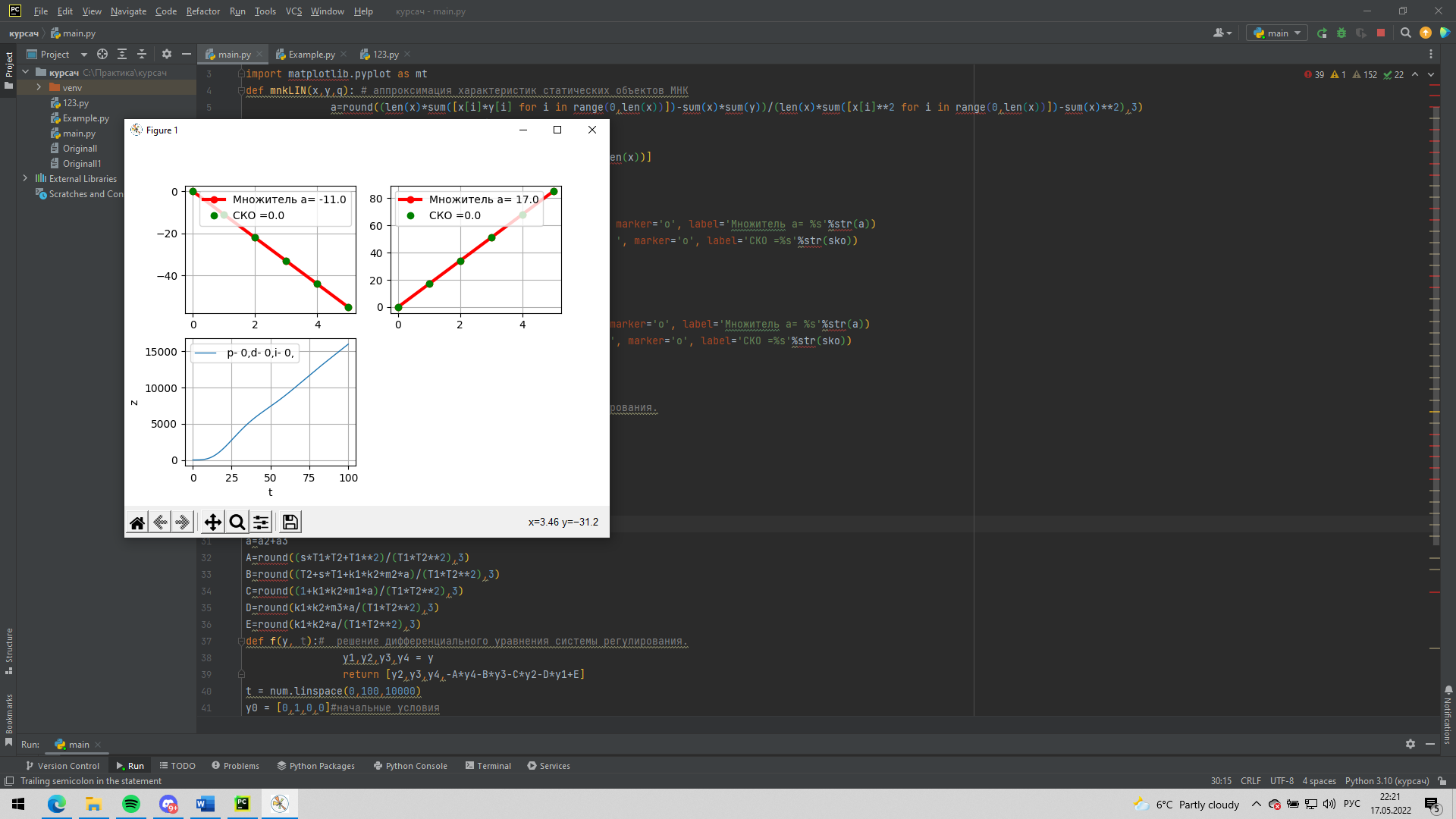
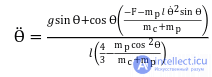пид регулятор. пид регуляторы и их применение в робототехнике
 Скачать 3.14 Mb. Скачать 3.14 Mb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ ЭКОНОМИЧЕСКИЙ УНИВЕРСИТЕТ (РИНХ)» ТАГАНРОГСКИЙ ИНСТИТУТ ИМЕНИ А.П. ЧЕХОВА Факультет физики, математики, информатики Кафедра информатики КУРСОВАЯ РАБОТА на тему: «ПИД регуляторы и их применение в робототехнике» Выполнила студентка группы ПИ-141 О.Д. Ляпина Направление подготовки «Прикладная информатика» Профиль подготовки «Прикладная информатика в менеджменте» Научный руководитель Р.И.Голуб Дата сдачи «___» __________2023г. Дата защиты «___» __________2023г. Оценка ________________ Таганрог 2023 ОглавлениеВведение 4 ПИД-регулятор 5 Методы применение ПИД-регулятора 7 Теоретический принцип работы ПИД-регулятора. 12 Пример работы ПИД-регулятора в робототехнике. 15 1. Обзор существующих решений 15 2. Постановка задачи 17 3. Математическая модель 18 4. Постановка эксперимента 19 5. Алгоритм работы 20 20 Недостатки использования ПИД-регуляторов 21 Пояснительная записка: 22 Код программы: 23 Список литературы: 26 ВведениеPython в русском языке встречаются названия пито́н или па́йтон) — высокоуровневый язык программирования общего назначения с динамической строгой типизацией и автоматическим управлением памятью, ориентированный на повышение производительности разработчика, читаемости кода и его качества, а также на обеспечение переносимости написанных на нём программ. Язык является полностью объектно-ориентированным в том плане, что всё является объектами. Необычной особенностью языка является выделение блоков кода пробельными отступами. Синтаксис ядра языка минималистичен, за счёт чего на практике редко возникает необходимость обращаться к документации[27]. Сам же язык известен как интерпретируемый и используется в том числе для написания скриптов. Недостатками языка являются зачастую более низкая скорость работы и более высокое потребление памяти написанных на нём программ по сравнению с аналогичным кодом, написанным на компилируемых языках, таких как C или C++. Python является мультипарадигмальным языком программирования, поддерживающим императивное, процедурное, структурное, объектноориентированное программирование, метапрограммирование и функциональное программирование.Задачи обобщённого программирования решаются в основном за счёт динамической типизации. Аспектно-ориентированное программирование частично поддерживается через декораторы, более полноценная поддержка обеспечивается дополнительными фреймворками. Такие методики как контрактное и логическое программирование можно реализовать с помощью библиотек или расширений. Основные архитектурные черты — динамическая типизация, автоматическое управление памятью, полная интроспекция, механизм обработки исключений, поддержка многопоточных вычислений с глобальной блокировкой интерпретатора,высокоуровневые структуры многих данных. Поддерживается разбиение программ на модули, которые, в свою очередь, могут объединяться в пакеты. ПИД-регуляторЧто такое ПИД-регулятор: Пропорционально-интегрально-дифференцирующий (ПИД) регулятор — устройство в управляющем контуре с обратной связью. Используется в системах автоматического управления для формирования управляющего сигнала с целью получения необходимых точности и качества переходного процесса. ПИД-регулятор формирует управляющий сигнал, являющийся суммой трёх слагаемых, первое из которых пропорционально разности входного сигнала и сигнала обратной связи (сигнал рассогласования), второе — интегралу сигнала рассогласования, третье — производной сигнала рассогласования. Если какие-то из составляющих не используются, то регулятор называют пропорционально-интегрирующим, пропорционально-дифференцирующим, пропорциональным и т. д. Пропорциональная составляющая вырабатывает выходной сигнал, противодействующий отклонению регулируемой величины от заданного значения, наблюдаемому в данный момент времени. Он тем больше, чем больше это отклонение. Если входной сигнал равен заданному значению, то выходной равен нулю. Однако при использовании только пропорционального регулятора значение регулируемой величины никогда не стабилизируется на заданном значении. Существует так называемая статическая ошибка, которая равна такому отклонению регулируемой величины, которое обеспечивает выходной сигнал, стабилизирующий выходную величину именно на этом значении. Например, в регуляторе температуры выходной сигнал (мощность нагревателя) постепенно уменьшается при приближении температуры к заданной, и система стабилизируется при мощности, равной тепловым потерям. Температура не может достичь заданного значения, так как в этом случае мощность нагревателя станет равна нулю, и он начнёт остывать. Чем больше коэффициент пропорциональности между входным и выходным сигналом (коэффициент усиления), тем меньше статическая ошибка, однако при слишком большом коэффициенте усиления при наличии задержек (запаздывания) в системе могут начаться автоколебания, а при дальнейшем увеличении коэффициента система может потерять устойчивость. Интегрирующая составляющая пропорциональна интегралу по времени от отклонения регулируемой величины. Её используют для устранения статической ошибки. Она позволяет регулятору со временем учесть статическую ошибку. Если система не испытывает внешних возмущений, то через некоторое время регулируемая величина стабилизируется на заданном значении, сигнал пропорциональной составляющей будет равен нулю, а выходной сигнал будет полностью обеспечиваться интегрирующей составляющей. Тем не менее, интегрирующая составляющая также может приводить к автоколебаниям при неправильном выборе её коэффициента. Дифференцирующая составляющая пропорциональна темпу изменения отклонения регулируемой величины и предназначена для противодействия отклонениям от целевого значения, которые прогнозируются в будущем. Отклонения могут быть вызваны внешними возмущениями или запаздыванием воздействия регулятора на систему. Методы применение ПИД-регулятораПрактика применения Теоретические методы анализа системы с ПИД-регулятором редко применяются на практике. Основная сложность практического применения — незнание характеристик объекта управления. Кроме того, существенную проблему представляют нелинейность и нестационарность системы. Практические регуляторы работают в ограниченном сверху и снизу диапазоне, поэтому в принципе нелинейны. В этой связи получили распространение методы экспериментальной настройки регулятора, подключенного к объекту управления. Прямое использование формируемой алгоритмом управляющей величины также имеет свою специфику. Например, при регулировке температуры часто управляют не одним, а двумя устройствами, одно из них управляет подачей горячего теплоносителя для нагрева, а другое управляет хладагентом для охлаждения. Часто рассматриваются три варианта практических регуляторов. В первом варианте, наиболее близком к теоретическому описанию, выход регулятора — непрерывная аналоговая ограниченная величина. Во втором случае выход представляет собой поток импульсов, который может управлять шаговым двигателем. В третьем случае выходной управляющий сигнал регулятора используется для широтно-импульсной модуляции. В современных системах автоматизации, которые, как правило, строятся на базе PLC ПИД-регуляторы реализуются либо как специализированные аппаратные модули, включаемые в состав управляющего контроллера, либо программными методами, с применением специализированных библиотек. Производители контроллеров часто разрабатывают специализированное ПО (тюнеры) для настройки коэффициентов регулятора. Методы параметрической оптимизации Все методы параметрической оптимизации, используемые для настройки коэффициентов регулятора, можно классифицировать следующими признаками. 1.Точные Поисковые Беспоисковые 2. Приближенные Работающие он-лайн Работающие оф-лайн Метод Дудникова Е. Г Метод относится к точным поисковым методам оптимизации. Наиболее совершенный метод настройки регуляторов, который дает оценку запаса устойчивости по распределению корней характеристического уравнения. Системы управления должны иметь определённый запас устойчивости, соответственно иметь интенсивность ослабления вибрации и колебаний. Степень затухания колебаний зависит от пары комплексных корней характеристического уравнения. Они связаны определённым соотношением и в нём присутствует корневой показатель колебательности. Благодаря большому количеству достоинств метод признан традиционным. Он подходит как для настройки одноконтурных так и многоконтурных систем. Он надежен и достоверно проверен, однако имеет и недостатки. Основными из них являются: отсутствие рекомендаций по настройке алгоритмов ПДД и ПИДД-регуляторов и необходимость проведения итерационной процедуры поиска настроек при минимизации квадратичного критерия качества. Метод Ротача В. Я Метод Ротача относится к точным поисковым методам. Имеет идеологическую схожесть с методом Дудникова Е. Г. В нём рассматривается оценка запаса устойчивости систем управления по частотным характеристикам. Была выведена следующая закономерность: замкнутый контур будет удовлетворять требуемому запасу устойчивости, если комплексно-частотная характеристика разомкнутого не пересекает область, которая ограничена окружностью, характеризующую частотный показатель колебательности. Метод обладает следующими недостатками: не дает рекомендаций по расчету ПД, ПДД и ПИДД алгоритмов, не удовлетворяет результаты по запасу устойчивости и требует определённого количества итерационных процессов поиска. Метод В.Р.Сабанина и Н.И.Смирнова Метод классифицируется как точный поисковой метод. Вычисляются значения целевой функции в соответствии с имитационной моделью системы регулирования. Обеспечить необходимый запас устойчивости помогает частотный показатель колебательности. Определяется как максимальная частотная характеристика замкнутого АЧХ на резонансной частоте. Для оценки качества регулирования в цифровой процедуре оптимизация использует интегральный модульный критерий. Большим достоинством является возможность расчета подстроечных коэффициентов для алгоритмов ПИДД регулирования. К недостаткам относится: необходимость наличия специализированной программы для расчета и неизвестность изначального значения показателя колебательности. Метод многомерного сканирования Вишняковой Ю. Н. Метод также принадлежит группе поисковых точных методов. Суть метода многомерного сканирования заключается в последовательном переборе точек в пространстве параметров конфигурации. Шаг фиксируется и расчет проводится в каждой точке критерия оптимизации и проверки ограничений запаса устойчивости для всех составляющих системы. Затем из полученного массива параметров выбираются значения, при которых достигается наименьший минимум. Эти параметры будут оптимальными. Метод многомерного сканирования требует множественных вычислений (особенно, когда дело доходит до поиска глобального минимума в мультиэкстремальных проблемах) из-за необходимости повторять вычисления несколько раз в одном и том же алгоритме. Это является главным недостатком. Метод определения настроек по номограммам. Этот метод последний представитель точных поисковых методов. Существуют номограммы для определения настроек И- П- ПИ- и ПИД-регуляторов для объекта 1-го и 2-го порядка с запаздыванием. Номограммы позволяют определить предварительные настройки регуляторов устойчивых и нейтральных объектов для переходных процессов: апериодический, с 20%-ным перерегулированием, с минимальной квадратичной площадью отклонения. Достоинством метода является точность определения настроек регулятора, в связи с учётом нелинейной зависимости между параметрами настройки регулятора и величиной отношения величины запаздывания к постоянной времени объекта. Метод масштабирования. Метод относится к условно беспоисковым методам. Суть метода заключается в использовании имеющийся информации об эталонной САР с другим объектом управления, но с тем же регулятором, что и в настраиваемой замкнутой системе. Алгоритм состоит из следующих этапов: Аппроксимация эталонного и действительного объектов управления математической моделью. Введение искусственной системы координат и определение масштабных коэффициентов, связывающих между собой координаты реальной и искусственной систем. Перевод эталонных настроек регулятора из искусственной системы координат в реальную с помощью ранее определённых масштабных коэффициентов. Основным недостатком является необходимость наличия эталонных САР. А основным достоинством является универсальность метода для любого закона регулирования без исключения. Метод Циглера-Никольса. Этот метод представляет собой приближенный метод настройки. Является одним из наиболее известных. Принцип настройки состоит в следующем: необходимо вывести систему на границу устойчивости, пока в контуре не возникнут незатухающие колебания. Автоколебания достигаются за счет нулевого значения И- и Д- составляющих и путем подбора коэффициента передачи. Зафиксировав значение коэффициента передачи, период автоколебаний и амплитуду, по эмпирическим формулам вычисляются параметры настройки регулятора. Достоинством метода является его простота, а основным недостатком — неучитывание требований к запасу устойчивости. Метод Чина-Хронеса-Ресвика. Метод Чина-Хронеса-Ресвика является модифицированным методом Циглера-Никольса. Он позволяет получить большой запас устойчивости, но меньший коэффициент передачи. Настройки по Чину-Хронесу-Ресвику требуют подстройки преимущественно дифференциальной составляющей. Основными преимуществами является простота настройки и меньшее время настройки. Недостатки схожи с методом Циглера-Никольса: неполнота информации о запасе устойчивости системы, который определяет надёжность работы регулятора, и приближенная настройка. Метод Куна— «правило Т-суммы». Метод относится к методам оф-лайн настройки. Он ориентирован на объекты с S-образной переходной характеристикой. Параметром, характеризующим быстродействие рассматриваемых объектов, является суммарная постоянная времени TΣ. Эта величина TΣ может быть получена непосредственно из ответной реакции на ступенчатый входной сигнал системы. При этом TΣ прямо пропорционально площади над S-образной переходной характеристикой. Преимущественно, что величину TΣ можно определить при значительных помехах в измерении. Преимуществами являются быстрая настройка и достаточно хорошие результаты (в связи с «осторожной настройкой»), но при высоком порядке системы есть заметное перерегулирование. Метод Латцеля— бетрагсадаптация. Используя метод Латцеля — бетрагсадаптация нельзя напрямую определить параметры настройки системы имея ее переходную функцию. Такая возможность отсутствует, так как этот метод относится к табличным. Поиск параметров регулятора происходит путем расчета характеристических коэффициентов, которые получают в процессе интегрирования переходной функции. Этот метод неудобен для ручной настройки регуляторов. Достоинством метода является возможность настройки адаптивных приборов регулирования, а также обеспечение высокой точности настройки. Основной недостаток: трудоемкость из-за использования табличной информации. Теоретический принцип работы ПИД-регулятора.Назначение ПИД-регулятора — в поддержании заданного значения r некоторой величины y с помощью изменения другой величины u. Значение r называется заданным значением (или уставкой, в технике), а разность e = (r − y) — невязкой (или ошибкой [регулирования], в технике), рассогласованием или отклонением величины от заданной. Приведённые ниже формулы справедливы в случае линейности и стационарности системы, что редко выполняется на практике. Система управления с обратной связью с участием ПИД-регулятора. Система управляет величиной y(t), то есть выводит величину y(t) на заданное извне значение r(t). На вход ПИД-регулятора подаётся ошибка e(t), выход ПИД-регулятора является управляющим воздействием u(t) для некоторого процесса (для объекта управления), управляющего величиной y(t).  Рисунок 1 Выходной сигнал регулятора u определяется тремя слагаемыми:  где Кp, Кi, Кd — коэффициенты усиления пропорциональной, интегрирующей и дифференцирующей составляющих регулятора соответственно. Большинство методов настройки ПИД-регуляторов используют несколько иную формулу для выходного сигнала, в которой на пропорциональный коэффициент усиления умножены также интегрирующая и дифференцирующая составляющие:  В дискретной реализации метода расчета выходного сигнала уравнение принимает следующую форму: {\displaystyle U(n)=K_{p}E(n)+K_{p}K_{ip}T\sum _{k=0}^{n}{E(k)}+{\frac {K_{p}K_{dp}}{T}}(E(n)-E(n-1))} где {\displaystyle T}Т — время дискретизации. Используя замену:  В программной реализации для оптимизации расчетов переходят к рекуррентной формуле: Часто в качестве параметров ПИД-регулятора используются: -относительный диапазон:  -постоянные интегрирования и дифференцирования, имеющие размерность времени:  Следует учитывать, что термины используются по-разному в различных источниках и разными производителями регуляторов. Пример работы ПИД-регулятора в робототехнике. 1. Обзор существующих решений Рассмотрим основные конструктивные, структурно-функциональные особенности, а также области применения существующих балансирующих двухколесных роботов. nBot (рис. 1) использует акселерометр для получения значения угла наклона и гироскоп для получения скорости изменения угла наклона. Используется фильтр Вайнера (Weiner) для объединения сигналов этих двух сенсоров в один. Формула балансировки: На двигатель подается напряжение, пропорциональное углу наклона , угловой скорости , положению шасси и его скорости . Поворот осуществляется за счет добавления значения напряжения к одному двигателю, и вычитания его из другого. Таким образом, робот может поворачивать, сохраняя баланс. Движение по прямой осуществляется с помощью добавления значения к углу баланса . JOE (рис. 2) разрабатывался как мини-прототип транспортного средства для перевозки людей. Для стабилизации используется регулятор пространства состояний, который получает информацию от гироскопа и энкодеров двигателей .  Рисунок 1 - nBot Рисунок 2 - JOE Робот, созданный Питером Миллером (Peter Miller) получает значение о положении шасси с помощью энкодеров двигателей, значение скорости с помощью дифференцирования значения положения. Гироскоп и акселерометр, объединенные фильтром Калмана позволяют получить точное значение скорости и угла наклона без потери точности со временем. Управление происходит за счет нелинейной системы на нечеткой логике, распределяющей сигналы управления на двигатель каждого из колес .  Ballbot (рис. 3) – робот, балансирующий на шаре. Разрабатывался для взаимодействия с людьми. Система управления (рис. 4) представляет собой два контура: внутренняя – PI регулятор, внешняя – линейно-квадратичный регулятор .  Segway (рис. 5) – коммерчески доступная платформа, использующаяся в качестве транспорта на относительно небольшие расстояния в различных областях, начиная от туризма и заканчивая полицейскими патрулями. EN-V (рис. 6) – Концепт двухколесного автомобиля, разработанный компанией Segway совместно c General Motors. В отличие от других неустойчивых двухколесных роботов, управление осуществляется за счет перемещения груза, которое приводит к смещению центра тяжести относительно колесной оси . В большинстве роботов угол наклона рассчитывается путем интегрирования величины угловой скорости, полученной с помощью гироскопа и корректируется последовательным приближением к углу, вычисленному из показаний акселерометров . Одновременно все параметры обрабатываются фильтром Калмана. |