Урок пирамида. Пирамида. Ключевые задачи
 Скачать 431.5 Kb. Скачать 431.5 Kb.
|
|
Урок 8 ПИРАМИДА. КЛЮЧЕВЫЕ ЗАДАЧИ Цель: рассмотреть свойства пирамид, имеющих равные боковые ребра; равные апофемы. Ход урока I. Объяснение нового материала. 1. Вершина пирамиды проецируется в центр описанной около основания окружности, если: а) боковые ребра пирамиды равны; б) боковые ребра составляют с плоскостью основания равные углы; в) боковые ребра составляют с высотой пирамиды равные углы. Доказать. Составить обратные задачи. Доказать. 2. Вершина пирамиды проецируется в центр вписанной в основание окружности, если: а) апофемы равны; б) двугранные углы при ребрах основания равны; в) апофемы составляют с высотой пирамиды равные углы. Доказать. Составить обратные задачи. Доказать. II. Решение задач: №№ 246, 248, 250, 251. Домашнее задание: теория (знать ключевые задачи), №№ 247, 249, 252. Контрольные вопросы 1. Боковые ребра пирамиды равны между собой. Может ли основание пирамиды быть: 1) ромбом; 2) прямоугольником; 3) правильным шестиугольником? 2. Боковые ребра пирамиды равны между собой. Как расположена проекция вершины пирамиды на основании, если основание: 1) прямоугольник; 2) прямоугольный треугольник? 3. Двугранные углы при основании пирамиды равны между собой. Может ли в основании пирамиды быть: 1) равнобедренный треугольник; 2) ромб; 3) прямоугольник? 4. Вершина пирамиды проектируется в точку пересечения диагоналей основания. Что можно сказать о двугранных углах при основании пирамиды, если основание: 1) параллелограмм; 2) ромб; 3) равнобедренная трапеция?    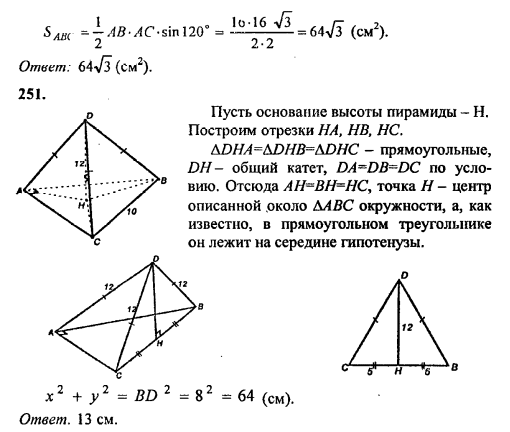 |
