лифт. План Введение краткий обзор существующих автоматизированных ситема управления (в том числе патентная информация) глубина патентной информации 5 лет. 4
 Скачать 1.17 Mb. Скачать 1.17 Mb.
|
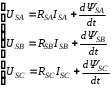 (2.1) (2.1)для цепей статора и 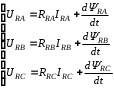 (2.2) (2.2)для цепей ротора. В представленных системах уравнений приняты следующие обозначения: 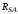 = =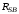 = =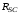 = =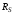 – активные сопротивления фаз статора; – активные сопротивления фаз статора;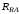 = =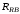 = =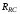 = =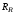 – активные сопротивления фаз ротора; – активные сопротивления фаз ротора;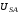 , , 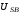 , , 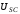 , , 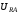 , , 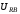 , , 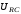 – мгновенные фазные напряжения статора и ротора; – мгновенные фазные напряжения статора и ротора;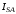 , , 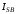 , , 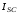 , , 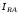 , , 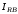 , , 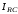 – мгновенные фазные токи в обмотках статора и ротора; – мгновенные фазные токи в обмотках статора и ротора;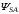 , , 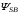 , , 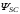 , , 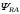 , , 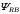 , , 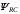 – потокосцепления обмоток статора и ротора. – потокосцепления обмоток статора и ротора.Для связи между потокосцеплениями и токами в обмотках воспользуемся законом Ампера, тогда: 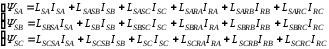 (2.3) (2.3)для статора 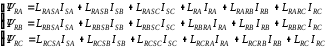 (2.4) (2.4)для ротора. Уравнения потокосцеплений показывают зависимость от токов в каждой обмотке через взаимоиндукцию. В уравнениях (2.3 и 2.4) коэффициенты 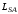 , , 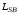 , , 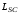 , , 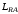 , , 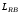 , , 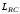 являются собственными индуктивностями соответствующих обмоток, все остальные – индуктивности между соответствующими обмотками. являются собственными индуктивностями соответствующих обмоток, все остальные – индуктивности между соответствующими обмотками.Не забывая о том, что системы уравнений (2.1 – 2.4) связывают исключительно скалярные величины, выражение для электромагнитного момента представим в следующем виде [60]: 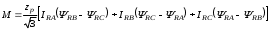 ,(2.5) ,(2.5)где 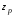 это число пар полюсов рассматриваемого АД. это число пар полюсов рассматриваемого АД.На основании второго закона Ньютона представим уравнение для движения и равновесия моментов на валу АД: 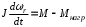 ,(2.6) ,(2.6)где 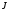 – момент инерции на валу АД, – момент инерции на валу АД, 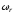 – угловая частота вращения ротора, – угловая частота вращения ротора, 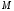 – момент развиваемый АД и – момент развиваемый АД и 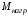 – момент приложенный к валу двигателя со стороны нагрузки. – момент приложенный к валу двигателя со стороны нагрузки.Изначально АД является трёхфазной электрической машиной с неявнополюсным ротором. Анализируя режимы работы АД в составе нагрузочного моментного ЭП и совокупность принятых выше допущений можно предположить правомерность использования для математического описания эквивалентной двухфазной модели. На пути упрощения математического описания АД оказался подходящим метод пространственного вектора, позволяющий существенно упростить и сократить вышеприведённую систему уравнений; метод позволяет связать уравнения (2.1 – 2.6) в единую систему с векторными переменными состояния. Суть метода состоит в том, что мгновенные значения симметричных трёхфазных переменных состояния (напряжение, токи, потокосцепления) можно математически преобразовать так, чтобы они были представлены одним пространственным вектором. Представим систему уравнений с векторными переменными состояния для случая с произвольной ориентацией системы координат [21, 36]: 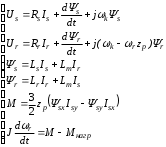 (2.7) (2.7)Здесь 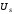 , , 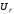 , , 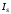 , , 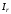 , , 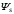 и и 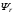 - двухэлементные векторы напряжений, токов и потокосцеплений, представленные в произвольно ориентированной ортогональной (двухфазной) системе координат в виде составляющих по координатным осям. Переменная - двухэлементные векторы напряжений, токов и потокосцеплений, представленные в произвольно ориентированной ортогональной (двухфазной) системе координат в виде составляющих по координатным осям. Переменная 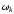 служит для задания произвольной частоты вращения координатной системы. Вспомогательная матричная константа j служит для «переворота» компонентов векторных переменных и позволяет упростить форму записи системы уравнений. служит для задания произвольной частоты вращения координатной системы. Вспомогательная матричная константа j служит для «переворота» компонентов векторных переменных и позволяет упростить форму записи системы уравнений.Раскрывая содержание пространственных векторов, получаем следующее: 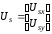 , ,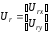 , ,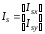 , ,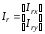 , ,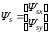 , , 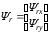 , , 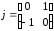 .(2.8) .(2.8)Система координат с принудительной ориентацией по вектору потокосцепления ротора При решении задач разработки систем управления для АД необходимо рассматривать его имитационную модель с позиций объекта оптимального управления. В теории систем управления асинхронными электроприводами при моделировании АД нашел место уникальный принцип ориентации системы координат по вектору потокосцепления ротора. В данном случае имитационная модель АД приобретает определенное сходство со структурной схемой машины постоянного тока, где возможно раздельное управление магнитным состоянием и моментом на валу двигателя. Математически условие ориентации применительно выражается следующим образом: 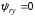 ; ;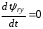 ; ;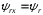 . .Уравнения, описывающие АД в системе координат с принудительной ориентацией по вектору потокосцепления ротора. 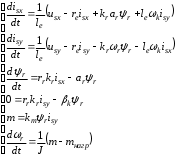 В системе 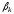 представляет собой скольжение системы координат, а представляет собой скольжение системы координат, а 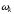 соответственно скорость её вращения. Данные параметры определяются в соответствии со следующими выражениями: соответственно скорость её вращения. Данные параметры определяются в соответствии со следующими выражениями: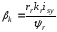 ; ;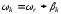 . .В системе уравнений переменные с индексами «x» и «y» соответствуют компонентам пространственного вектора в координатной системе с ориентацией по вектору потокосцеплений ротора 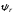 . С помощью правил создания и преобразования структурных схем, принятых в теории автоматического управления , представим систему уравнений в виде структурной схемы. На рис. представлена структурная схема, имитационной модели АД в системе координат с ориентацией по вектору потокосцепления ротора . С помощью правил создания и преобразования структурных схем, принятых в теории автоматического управления , представим систему уравнений в виде структурной схемы. На рис. представлена структурная схема, имитационной модели АД в системе координат с ориентацией по вектору потокосцепления ротора 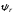 . .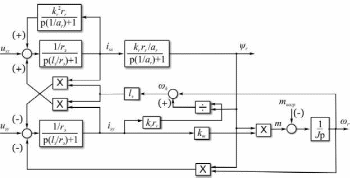 Рисунок 6 - Структурная схема имитационной модели АД в системе координат с ориентацией по вектору потокосцепления ротора  Модель АД, представленная на рис. удобна для реализации и расчёта в любом из прикладных программных продуктов, поддерживающих объектно-структурное моделирование систем (Simulink-Matlab, Windora и т.д.). Для исследования и проверки адекватности созданной модели АД удобно выполнить её реализацию в среде Simulink-Matlab. В данной системе симметричные трёхфазные напряжения, представленные в относительных единицах подвергаются преобразованию Кларка и поступают в виде компонентов пространственного вектора напряжений 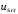 и и 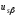 на входы координатного преобразователя Парка-Горева. Формулы для координатного преобразования Парка-Горева, позволяющего реализовать переход от стационарной системы координат к вращающейся представлены ниже: на входы координатного преобразователя Парка-Горева. Формулы для координатного преобразования Парка-Горева, позволяющего реализовать переход от стационарной системы координат к вращающейся представлены ниже: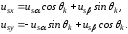 Здесь 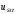 , , 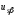 - составляющие пространственного вектора напряжения статора - составляющие пространственного вектора напряжения статора 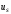 , представленные в стационарной системе координат; , представленные в стационарной системе координат;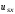 , , 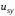 - составляющие вектора напряжения статора - составляющие вектора напряжения статора 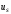 , представленные во вращающейся системе координат; , представленные во вращающейся системе координат;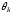 - угол поворота вращающейся координатной системы (угол ориентации). Параметр - угол поворота вращающейся координатной системы (угол ориентации). Параметр 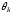 связан с угловой скоростью вращения координатной системы связан с угловой скоростью вращения координатной системы 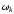 благодаря следующему выражению: благодаря следующему выражению: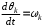 . .Графически преобразование Парка-Горева иллюстрируется на рис. 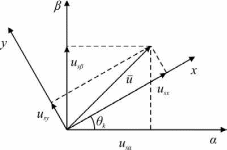 Рис. График преобразований Парка-Горева для связи между вращающейся и стационарной системой координат Координатный преобразователь Парка-Горева сориентирован совместно с системой координат разработанной имитационной модели АД. Благодаря этому на входы модели по напряжению 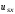 и и 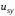 поступают компоненты пространственного вектора напряжения, представленного во вращающейся системе координат. поступают компоненты пространственного вектора напряжения, представленного во вращающейся системе координат.3.2 Структура и параметрический синтез регуляторов системы управления ТП Синтез регуляторов производился из стандартной методики настройки контуров на модульный или симметричный оптимум. Далее приведём лишь передаточные функции регуляторов и краткое описание контуров. Контур тока. Настройка контура тока проводилась на модульный оптимум с помощью ПИ-регулятора. Передаточная функция ПИ-регулятора тока 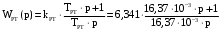 . .Коэффициент усиления регулятора тока: 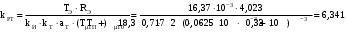 , ,где 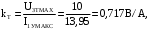 коэффициент ОС по току. 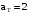 - коэффициент оптимизации. - коэффициент оптимизации.Постоянная времени регулятора тока: 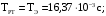 Настройка контура близка к настройке на модульный оптимум (МО) системы 2-го порядка. Контур является астатической системой 1-го порядка по управлению. Контур потокосцепления. При оптимизации контура потокосцепления внутренний оптимизированный замкнутый контур тока представлен усеченной передаточной функцией 1-го порядка. Передаточная функция ПИ-регулятора потокосцепления 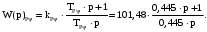 Коэффициент усиления и постоянная времени регулятора потокосцепления определяются по выражениям 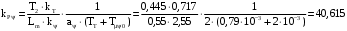 где 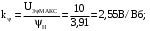 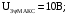 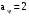 - коэффициент оптимизации. - коэффициент оптимизации.Настройка контура близка к настройке на модульный оптимум системы второго порядка. Контур является астатической системой регулирования первого порядка по управлению и обеспечивает нулевую установившуюся ошибку 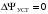 . .Контур скорости. При оптимизации контура скорости внутренний оптимизированный замкнутый контур тока представлен усеченной передаточной функцией 1-го порядка. Передаточная функция ПИ-регулятора: 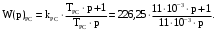 Коэффициент усиления и постоянная времени регулятора скорости определяются по выражениям: 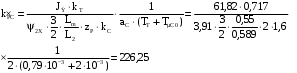 Оптимизированный контур при отработке ступенчатых управляющих воздействий обеспечивает высокое быстродействие при перерегулировании в общем случае более 43%. Настройка контура без фильтров на входе близка к настройке на СО. Для ограничения перерегулирования на уровне около 8,1 % на входе контура скорости включены два одинаковых фильтра. Нелинейная система. Дальнейшее моделирование проводилось с учётом основных нелинейностей – насыщение регуляторов, ограниченное напряжение преобразователя. К нелинейной системе для регулирования скорости предъявляются следующие требования: Постоянная скорость вращения равная 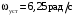 , что соответствует линейному движению кабины со скоростью , что соответствует линейному движению кабины со скоростью 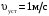 . .Ограничение ускарения. Ускорение должно быть 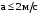 . .Чтобы выполнить выдвинутые требования необходим задатчик интенсивности, с помощью которого установим время разгона до рабочей скорости. 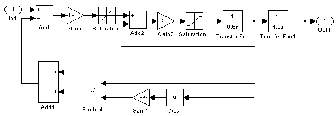 Рисунок 0.6 - Имитационная модель S-образного задатчика интенсивности в среде Simulink Пусть время разгона будет 2,4 с. 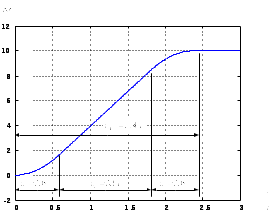 Рисунок 8 - – Переходная характеристика S-образного задатчика интенсивности. Имитационная модель РЭП в среде Simulink представлена на рисунке 9. Переходные характеристики полученные при моделировании представлены на рисунке 10. 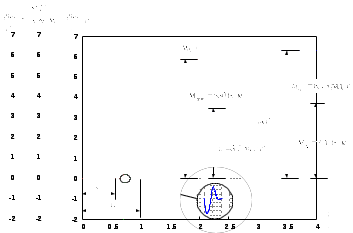 Рисунок 10 – Переходные характиристики нелинейной системы РЭП 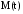 , , 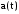 , , 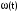 Ускорение ограничено на уровне 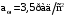 , что соответствует линейному ускорению , что соответствует линейному ускорению 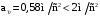 . .В САУ СЭП при использовании пропорционального регулятора в позиционных режимах наблюдается перерегулирование, что критично для управления позиционирования кабины лифта. С целью оптимизации переходных процессов применяют регулятор положения с нелинейной характеристикой. В простейшей схеме второго порядка с ограничением момента (тока) двигателя это парабола. Параболический регулятор. Характеристику регулятора положения задаем в виде кусочно-линейной функции имеющей параболический вид: 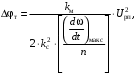 где 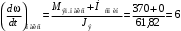 Определим точки линейного участка характеристики 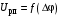 регулятора положения из выражения: регулятора положения из выражения: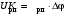 , ,где 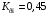 - коэффициент усиления регулятора положения. - коэффициент усиления регулятора положения.Решая систему уравнений 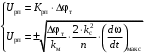 ,где n = 4, находим точку пересечения, где линейная характеристика регулятора переходит в плавное возрастание 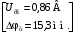 Таблица 3 - Характеристика 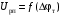
Рассмотрим отработку задания на передвижение на расстояние пятого этажа в одномассовой механической системе. С учётом расстояния между этажами равным 3 метра, задание составит 15000. Полученные переходные характеристики представлены на рисунке 11. |
