ДОМАШНЕЕ ЗАДАНИЕ
№
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
Ответ
|
50
|
40
|
30
|
20
|
80
|
60
|
40
|
20
|
ПЛОЩАДЬ ТРАПЕЦИИ
ЗАДАНИЕ 1. На клетчатой бумаге с размером клетки 1 см 1 см изображена трапеция. Найдите её площадь. Ответ дайте в квадратных сантиметрах.
ОБРАЗЕЦ:
а)
|
|
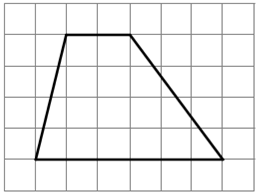
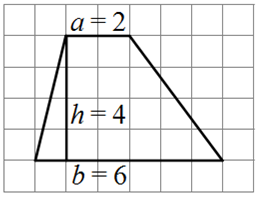
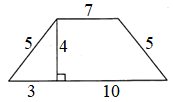
Проведём высоту в трапеции и по клеточкам посчитаем длины оснований а, b и высоты h.
После этого вычислим площадь:
|
|
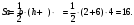
|
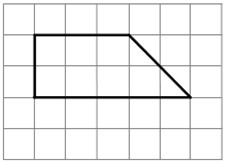
б)
|
|
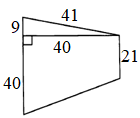
Трапеция прямоугольная, поэтому её высота совпадает с боковой стороной, прилежащей к прямому углу.
|
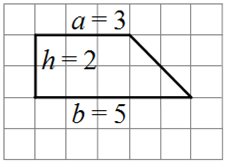
|
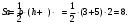
|
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1)
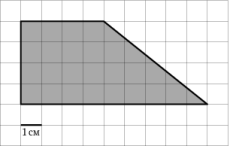
|
2)
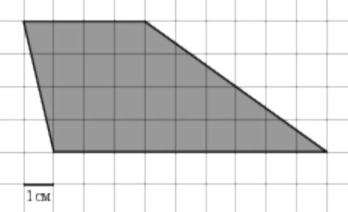
|
3)
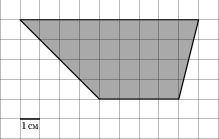
|
4)
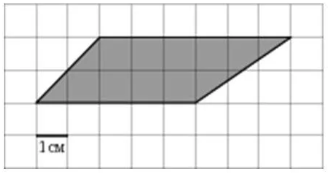
|
5)
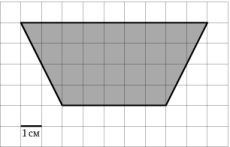
|
6)
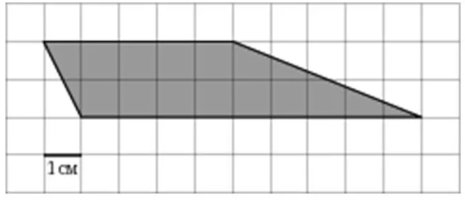
|
7)
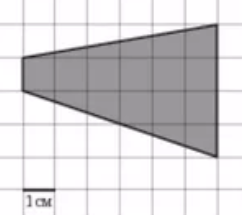
|
8)
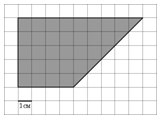
|
9)
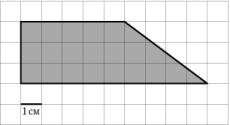
|
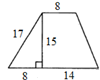
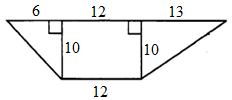
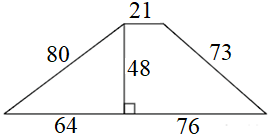
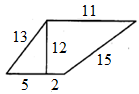
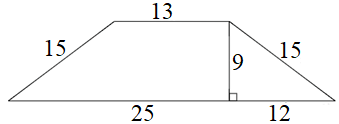
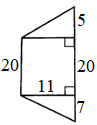
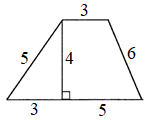
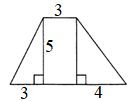
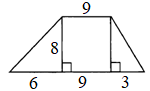
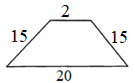
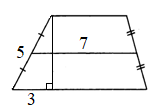
ЗАДАНИЕ 2. Найдите площадь трапеции:
|
|
|
1)
|
2)
|
3)
|
|
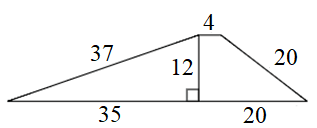
|
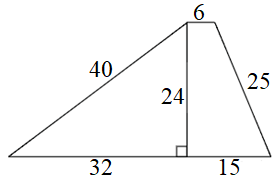
|
4)
|
5)
|
6)
|
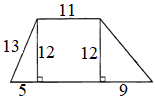
|
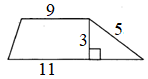
|
|
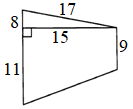
7)
|
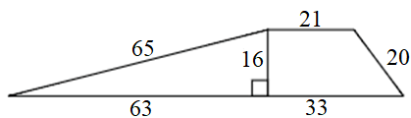
8)
|
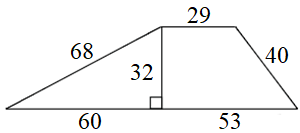
9)
|
|
|
|
10)
|
11)
|
12)
|
|
|
|
13)
|
14)
|
15)
|
|
|
|
16)
|
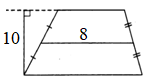
17)
|
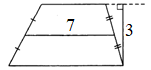
18)
|
|
|
|
19)
|
20)
|
21)
|
ДОМАШНЕЕ ЗАДАНИЕ
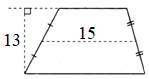
На клетчатой бумаге с размером клетки 1 см 1 см изображена трапеция. Найдите её площадь. Ответ дайте в квадратных сантиметрах.
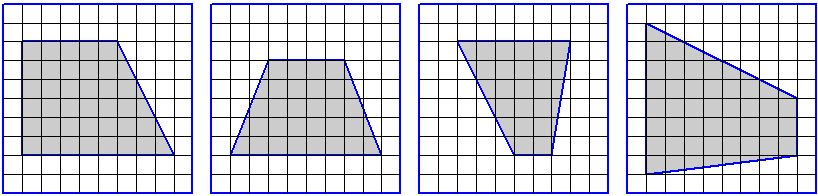
|
1
|
2
|
3
|
4
|
Найдите площадь трапеции:
ПЛОЩАДЬ ТРАПЕЦИИ (ОТВЕТЫ)
КЛАССНАЯ РАБОТА
ЗАДАНИЕ 1
№
|
Ответ
|
№
|
Ответ
|
№
|
Ответ
|
1
|
26
|
4
|
11
|
7
|
15
|
2
|
26
|
5
|
28
|
8
|
32,5
|
3
|
26
|
6
|
14
|
9
|
21
|
ЗАДАНИЕ 2
№
|
Ответ
|
№
|
Ответ
|
№
|
Ответ
|
1
|
225
|
8
|
36
|
15
|
32,5
|
2
|
215
|
9
|
225
|
16
|
108
|
3
|
3864
|
10
|
210
|
17
|
132
|
4
|
108
|
11
|
936
|
18
|
28
|
5
|
354
|
12
|
2272
|
19
|
80
|
6
|
636
|
13
|
286
|
20
|
21
|
7
|
216
|
14
|
22
|
21
|
195
|
ДОМАШНЕЕ ЗАДАНИЕ
№
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
Ответ
|
39
|
30
|
24
|
44
|
40
|
1400
|
1632
|
ПЛОЩАДЬ ПРОИЗВОЛЬНОЙ ФИГУРЫ НА КЛЕТЧАТОЙ БУМАГЕ
ЗАДАНИЕ. На клетчатой бумаге с размером клетки 1 см 1 см изображена фигура. Найдите её площадь. Ответ дайте в квадратных сантиметрах.
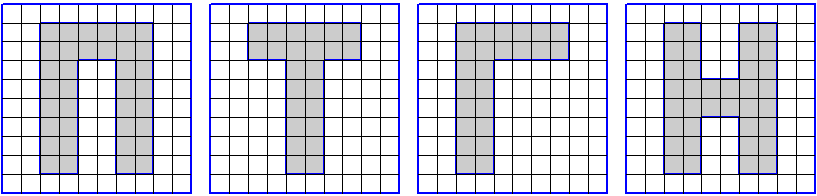
|
1
|
2
|
3
|
4
|
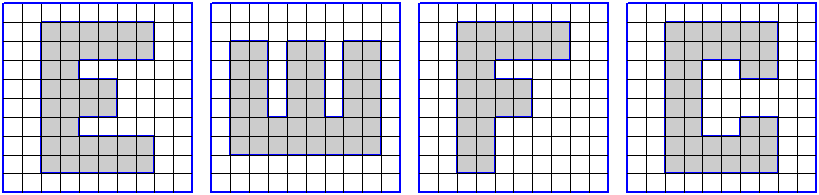
|
5
|
6
|
7
|
8
|
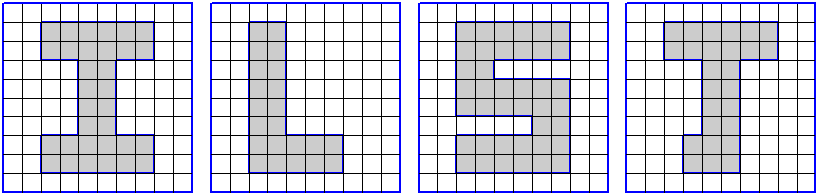
|
9
|
10
|
11
|
12
|
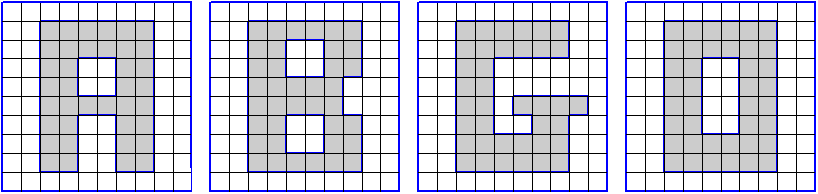
|
13
|
14
|
15
|
16
|
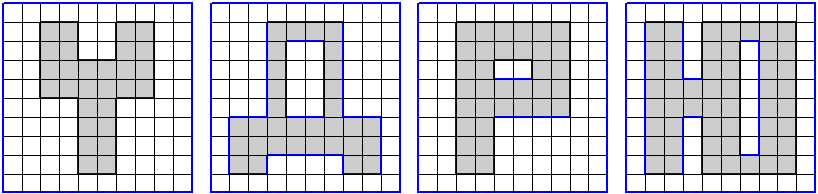
|
17
|
18
|
19
|
20
|
ПЛОЩАДЬ ПРОИЗВОЛЬНОГО ТРЕУГОЛЬНИКА НА КЛЕТКАХ
ЗАДАНИЕ. На клетчатой бумаге с размером клетки 1 см 1 см изображена фигура. Найдите её площадь. Ответ дайте в квадратных сантиметрах.
ОБРАЗЕЦ:
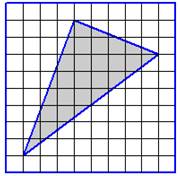
|
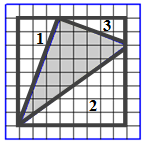
Площадь этого треугольника найти по формуле не получится, так как мы не знаем длин его сторон и проведённых к ним высот. Поэтому, для нахождения площади, достроим треугольник до прямоугольника (в рассматриваемом примере получился квадрат).
Найдём площадь получившегося квадрата: Sкв = 8 ∙ 8 = 64.
|
|
Видим, что при таком достраивании образовалось три прямоугольных треугольника. Найдём площади полученных фигур:
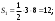 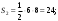 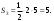 Для нахождения искомой площади, исключим из площади квадрата площади трёх треугольников: Для нахождения искомой площади, исключим из площади квадрата площади трёх треугольников:
|
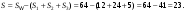
|
|
 Скачать 1.82 Mb.
Скачать 1.82 Mb.


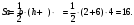

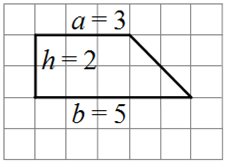
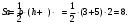






































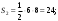
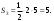 Для нахождения искомой площади, исключим из площади квадрата площади трёх треугольников:
Для нахождения искомой площади, исключим из площади квадрата площади трёх треугольников: