Тест Площади фигур. Площади фигур
 Скачать 33.33 Kb. Скачать 33.33 Kb.
|
|
Тест №1 по теме: «Площади фигур» II вариант Равные фигуры имеют ___ площади. Площадь прямоугольника со сторонами 8 и 10 равна _____. Стороны параллелограмма равны 10 см и 6 см, а угол между этими сторонами равен 30°. Чему равна площадь этого параллелограмма? _____. Сторона треугольника равна 15, а высота, проведенная к этой стороне равна 10. Площадь этого треугольника равна _______. Если сторона параллелограмма равна 17см, а его площадь 187см², то высота, проведённая к этой стороне равна _____. Площадь ромба со стороной 10 см и углом 60° равна ______. П 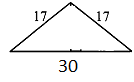 лощадь равнобедренного треугольника, изображенного на рисунке, равна ______. лощадь равнобедренного треугольника, изображенного на рисунке, равна ______.П 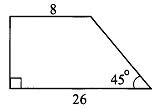 лощадь трапеции, изображенной на рисунке, равна _______. лощадь трапеции, изображенной на рисунке, равна _______.Если площадь круга равна 441π, то радиус круга ______. Площадь кругового сектора вычисляется по формуле _______. Формула радиуса описанной около треугольника окружности __. Тест №1 по теме: «Площади фигур» I вариант Если фигура разбита на части, то площадь этой фигуры равна ___. Площадь квадрата со стороной 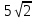 см равна _____. см равна _____.Чему равна площадь ромба, диагонали которого равны 10см и 12см? ______. Две стороны треугольника равны 12 см и 9 см, а угол между ними 60°. Чему равна площадь треугольника? ______. Если сторона треугольника 15см, а его площадь 75см2, то высота, проведенная к ней, равна ________. П 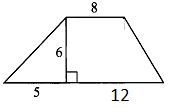 лощадь прямоугольного треугольника с гипотенузой 26 см и катетом 24 см равна _______. лощадь прямоугольного треугольника с гипотенузой 26 см и катетом 24 см равна _______.Площадь трапеции, изображенной на рисунке, равна _______. Сторона ромба равна 5, одна из диагоналей 6, то площадь ромба равна ______. Если площадь круга равна 169π, то диаметр круга ______. Площадь сегмента вычисляется по формуле ______. Формула радиуса вписанной в треугольник окружности _______. Тест №2 по теме: «Площади фигур» I вариант Если фигуры равны, то их площади будут равны. Площадь прямоугольника равна половине произведения смежных сторон Стороны параллелограмма равны 10 см и 6 см, а угол между этими сторонами равен 30°. Чему равна площадь этого параллелограмма? _____. Сторона треугольника равна 15, а высота, проведенная к этой стороне равна 10. Площадь этого треугольника равна _______. Если сторона параллелограмма равна 17см, а его площадь 187см², то высота, проведённая к этой стороне равна _____. Площадь ромба со стороной 10 см и углом 60° равна ______. П  лощадь равнобедренного треугольника, изображенного на рисунке, равна ______. лощадь равнобедренного треугольника, изображенного на рисунке, равна ______.П  лощадь трапеции, изображенной на рисунке, равна _______. лощадь трапеции, изображенной на рисунке, равна _______.Если площадь круга равна 441π, то радиус круга ______. Площадь кругового сектора вычисляется по формуле _______. Формула радиуса описанной около треугольника окружности __. Тест №2 по теме: «Площади фигур» II вариант Если фигура разбита на части, то площадь этой фигуры равна ___. Площадь квадрата со стороной 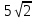 см равна _____. см равна _____.Чему равна площадь ромба, диагонали которого равны 10см и 12см? ______. Две стороны треугольника равны 12 см и 9 см, а угол между ними 60°. Чему равна площадь треугольника? ______. Если сторона треугольника 15см, а его площадь 75см2, то высота, проведенная к ней, равна ________. П  лощадь прямоугольного треугольника с гипотенузой 26 см и катетом 24 см равна _______. лощадь прямоугольного треугольника с гипотенузой 26 см и катетом 24 см равна _______.Площадь трапеции, изображенной на рисунке, равна _______. Сторона ромба равна 5, одна из диагоналей 6, то площадь ромба равна ______. Если площадь круга равна 169π, то диаметр круга ______. Площадь сегмента вычисляется по формуле ______. Формула радиуса вписанной в треугольник окружности _______. |
