кп6. Побудова економетричної моделі на основі системи одночастних структурних рівнянь
 Скачать 115.53 Kb. Скачать 115.53 Kb.
|
|
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ УКРАЇНИ “КИЇВСЬКИЙ ПОЛІТЕХНІЧНИЙ ІНСТИТУТ ІМЕНІ ІГОРЯ СІКОРСЬКОГО” Факультет менеджменту та маркетингу Комп’ютерний практикум №6 з дисципліни «Економетрика» на тему: «Побудова економетричної моделі на основі системи одночастних структурних рівнянь» Виконала: студентка групи УК-01 Шмуйло К.С. Перевірив: доц. Фартушний І.Д. Київ – 2022 ТЕОРЕТИЧНА ЧАСТИНА Система одночасних структурних рівнянь – всі рівняння, що найчастіше характеризують економічні процеси та явища, які відбуваються одночасно, а також мають спільний зв'язок. Економетрична модель на основі системи одночасних рівнянь: 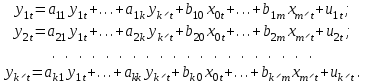 У цій моделі 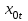 = 1. Окремі коефіцієнти = 1. Окремі коефіцієнти 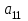 ..., ..., 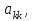 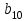 ..., ..., 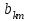 можуть дорівнювати нулю, якщо відповідна змінна не входить до рівняння. Залишки можуть дорівнювати нулю, якщо відповідна змінна не входить до рівняння. Залишки 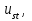 де s = 1, 2, ..., k, також можуть дорівнювати нулю, якщо відповідне рівняння є тотожністю. де s = 1, 2, ..., k, також можуть дорівнювати нулю, якщо відповідне рівняння є тотожністю. Систему можна переписати в матричній формі: 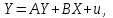 де Y — вектор ендогенних залежних змінних; X — матриця екзогенних пояснювальних змінних; u — вектор залишків; A — матриця коефіцієнтів для змінних Y розміром k × k; B — матриця коефіцієнтів для змінних X розміром k × m; k — кількість рівнянь в моделі 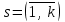 ; m — кількість екзогенних змінних ; m — кількість екзогенних змінних 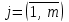 . .Змінні, які містяться у правій частині системи рівнянь, є наперед заданими і називаються екзогенними, а змінні, які містяться в лівій частині, знаходяться в результаті реалізації моделі і називаються ендогенними. Отже, змінна yst є ендогенною для одного рівняння і одночасно екзогенною для іншого. Економетрична модель у вигляді безпосередньо відображає структуру зв’язків між змінними і тому називається структурною формою економетричної моделі. Розв’яжемо систему рівнянь відносно yst і дістанемо систему виду: 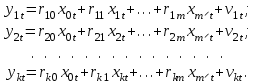 У матричній формі систему цих рівнянь можна переписати так: 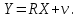 Матриця оцінок параметрів R має вигляд: 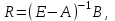 де E — одинична матриця. Щоб показати справедливість співвідношення, розв’яжемо систему рівнянь відносно Y: Y – AY = BX + u; (E – A)Y = BX + u; Y = (E – A)–1BX + u. Враховуючи, що Y = RX + v, R = (E – A)–1B. Вектор залишків 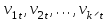 є лінійною комбінацією залишків є лінійною комбінацією залишків 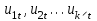 . .Економетрична модель, яка записується системою рівнянь, називається зведеною формою моделі. Оскільки економетрична модель складається з системи одночасних рівнянь, то постає запитання: чи можна застосувати для оцінювання параметрів кожного рівняння або системи в цілому ті методи, які були розглянуті в попередніх розділах? Проблеми чисельної оцінки параметрів в структурній формі і можливість перетворення структурної форми на зведену тісно пов’язані з поняттям ідентифікації моделі. Якщо лінійна комбінація рівнянь структурної форми не може привести до рівняння, що має ті самі змінні, що й деяке рівняння в структурній формі, то модель буде ідентифікованою. Для ідентифікованих моделей зведена форма визначається однозначно за допомогою співвідношень. Матриця E – A завжди невироджена. Умова ідентифікації має перевірятися для кожного рівняння системи. Алгоритм непрямого методу найменших квадратів Крок 1. Перевіряється умова ідентифікованості для кожного рівняння структурної форми моделі. Якщо кожне рівняння точно ідентифіковане, то переходимо до кроку 2. Крок 2. Кожне рівняння структурної форми розв’язується відносно однієї з k ендогенних змінних моделі, у результаті приходимо до зведеної форми моделі. Крок 3. Застосовуючи 1МНК, визначається оцінка параметрів окремо для кожного рівняння зведеної форми. Крок 4. Розраховується оцінка параметрів рівнянь структурної форми за допомогою співвідношення AR = –B, де A і B — параметри структурних рівнянь, а R — матриця оцінок параметрів зведеної форми. ПРАКТИЧНА ЧАСТИНА Ціль роботи: Навчитись будувати економетричні моделі на основі системи одночасних структурних рівнянь, оцінювати статистичну значущість характеристик зв’язку, визначити точковий та інтервальний прогнози ендогенних змінних. Завдання до комп’ютерного практикуму: На основі зведених даних по соціальній статистиці про економічну діяльність підприємств обслуговування населення Деснянської держадміністрації м. Києва за десять років сформовані часові ряди по наступних показниках: рівноважна кількість споживання продуктів,тис.грн.-У1; ціна одиниці продукції,грн.-У2; дохід на душу населення,грн.-Х1; витрати в середньому на виробництво одиниці продукції,грн.-Х2.Вихідна інформація задана в таблиці 1. Необхідно: 1. Ідентифікувати змінні моделі. 2. Провести специфікацію моделі на основі одночасових структурних рів-нянь. 3. Визначити індетифікованність кожного рівняння моделі. 4. Розрахувати оцінки параметрів моделі. 4.1. Перейти від структурної до приведенної форми рівнянь. 4.2. Розрахувати оцінки параметрів моделі методами 1МНК, НМНК, 2МНК, 3МНК. 4.3. Здійснити перехід від приведенної до структурної форми моделі. 5. Визначити асимптотичні стандартні помилки знайдених оцінок параметрів моделі. 6. Розрахувати прогнозні значення ендогенних змінних моделі на основі системи рівнянь. 7.Провести економічний аналіз одержанної інформації, сформувати висновки і пропозиції. ВАРІАНТ 10
Розв’язання: Y1 – рівноважна кількість споживання продуктів, тис. грн.. Y2 – ціна одиниці продукції, грн.. X1 – дохід на душу населення, грн.. X2 – витрати в середньому на виробництво одиниці продукції. Специфікація моделі на основі одночасових структурних рівнянь.Система одночасних структурних рівнянь – всі рівняння, що найчастіше характеризують економічні процеси та явища, які відбуваються одночасно, а також мають спільний зв'язок. Системи одночасних структурних рівнянь найчастіше включають лінійні рівняння, а нелінійні зв’язки, здебільшого, апроксимують лінійними співвідношеннями. Система одночасних структурних рівнянь у матричній формі може бути записана у вигляді: Y=AY+BX+U (1) Y - матриця-вектор залежних змінних X - матриця-вектор незалежних змінних U - матриця-вектор залишків A - матриця-вектор коефіцієнтів при Y, розмірності (k×k) B – матриця-вектор коефіцієнтів при X, розмірності (k×m) Y1t=A11*Y2t+ B10*Xot+B11*X1t+U1t Y2t=A21*Y1t+ B20*Xot+B22*X2t+U2t Економетрична модель (1) відображає структуру зв’язків між змінними, тому називається структурною формулою економетричної моделі. Ідентифікованність кожного рівняння моделі
Розрахуваємо оцінки параметрів моделі Розраховуємо оцінки параметрів моделі за методом 1МНК Для першого рівняння системи Y1t=A11*Y2t+ B10*Xot+B11*X1t+U1t Для другого рівняння системи Y2t=A21*Y1t+ B20*Xot+B22*X2t+U2t Перейдемо від структурної до приведенної форми рівнянь У структурній формі система рівнянь матиме вигляд: 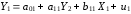 ;. ;.Перейдемо від структурної до приведеної форми рівнянь. Для цього в другому рівнянні замість 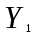 підставимо вираз у правій частині першого рівняння. підставимо вираз у правій частині першого рівняння.Запишемо: 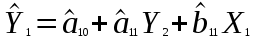 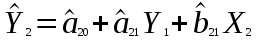 Підставимо значення 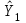 у друге рівняння, звідси: у друге рівняння, звідси: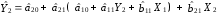 ; ;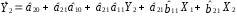 ; ;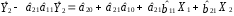 ; ;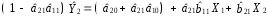 . .Розділимо обидві частини рівняння на 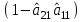 і отримаємо: і отримаємо: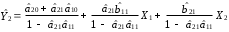 . .Замінимо 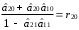 ; ;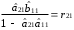 ; ;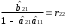 . .В результаті отримаємо друге рівняння моделі в приведеній формі: 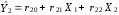 А тепер значення структурного рівняння 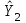 підставимо в перше рівняння моделі (2) і приведемо його до приведеної форми. підставимо в перше рівняння моделі (2) і приведемо його до приведеної форми.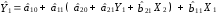 ; ;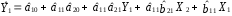 . .Перенесемо 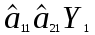 в ліву частину рівняння: в ліву частину рівняння: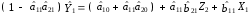 . .Розділимо обидві частини рівняння на 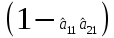 і отримаємо: і отримаємо: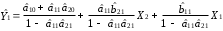 . .Замінимо: 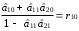 ; ;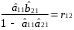 ; ;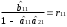 . .В результаті отримаємо перше рівняння моделі в приведеній формі: 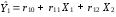 . .Таким чином, економетрична модель в приведеній формі: 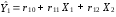 ; ;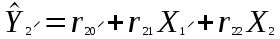 А за методом оцінки параметрів 1МНК за вище наведеними обрахунками отримаємо наступний запис моделі в приведеній формі: 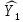 = 37,843 – 0,256 ∗ Х1 – 0,286 ∗ Х2 = 37,843 – 0,256 ∗ Х1 – 0,286 ∗ Х2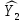 = -28,533 + 0,125 ∗ Х1 +1,359 ∗ Х2 = -28,533 + 0,125 ∗ Х1 +1,359 ∗ Х2Знайдемо коефіцієнти кореляції, детермінації, F-критерій Фішера та t- критерій для Y1 та Y2. Д 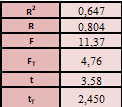 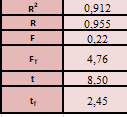 ля Y1: Для Y2: Розрахувати оцінки параметрів моделі методами 1МНК, НМНК, 2МНК, 3МНК.Оцінюємо параметри моделі методом 1МНК, так як рівняння нашої системи є точно ідентифікованими, то ми не можемо застосовувати 2МНК та 3МНК, а у методі НМНК виконується оцінка параметрів кожного рівняння зведеної форми моделі методом 1МНК. Здійснюємо перехід від приведеної до структурної форми: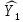 = -0,210 ∗ Y2 – 0,030 ∗ Х1 – 46,486 = -0,210 ∗ Y2 – 0,030 ∗ Х1 – 46,486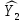 = 0,489 ∗ Y1 + 1,499 ∗ Х2 – 47,025 = 0,489 ∗ Y1 + 1,499 ∗ Х2 – 47,025Визначити асимптотичні стандартні помилки знайдених оцінок параметрів моделі.Для цього необхідні 4 матриці: Матриця Х: (стовпчик одиниць;стовпчик Х1; стовпчик Х2); Матриця Y: (стовпчик ендогенної змінної); Матриця Y(номер) : (стовпчик екзогенної змінної Y); 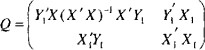 Матриця X(номер) : (стовпчик 1;стовпчик екзогенної змінної X); Складаємо блочну матрицю Q: Матриця X(номер) : (стовпчик 1;стовпчик екзогенної змінної X); Складаємо блочну матрицю Q:А також ще одну матрицю: Знаходимо матрицю А, вона дорівнює нижченаведеному добутку: 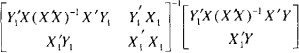 Знаходимо матрицю асимптотичних стандартних похибок, домножуючи матрицю Q-1 на σ2. Значення асимптотичних стандартних похибок дорівнює кореню з діагональних елементів матриці асимптотичних стандартних похибок. Детальні розрахунки описані в Excel-файлі:
Розрахувати прогнозні значення ендогенних змінних моделі на основі системи рівнянь.
ВИСНОВКИ Підсумовуючи виконану роботу можна дійти висновку, що рівняння даної системи є ідентифіковані, що свідчить про те, що неможливо використати 2МНК, 3МНК , у методі НМНК виконується оцінка параметрів кожного рівняння зведеної форми моделі методом 1МНК. Система у приведеній формі має вигляд: 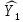 = 37,843 – 0,256 ∗ Х1 – 0,286 ∗ Х2 = 37,843 – 0,256 ∗ Х1 – 0,286 ∗ Х2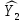 = -28,533 + 0,125 ∗ Х1 +1,359 ∗ Х2 = -28,533 + 0,125 ∗ Х1 +1,359 ∗ Х2У структурній формі має вигляд: 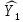 = -0,210 ∗ Y2 – 0,030 ∗ Х1 – 46,486 = -0,210 ∗ Y2 – 0,030 ∗ Х1 – 46,486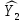 = 0,489 ∗ Y1 + 1,499 ∗ Х2 – 47,025 = 0,489 ∗ Y1 + 1,499 ∗ Х2 – 47,025Якщо проаналізувати коефіцієнт детермінації, кореляції, F та t критерії для Y1 та Y2 з приведеної форми, то: для Y1 коефіцієнт детермінації = 0,647, що свідчить про те що, тільки 0,647 частина варіації залежної змінної пояснена моделлю, коефіцієнт кореляції = 0,804 показує, що вплив змінної X на Y є помітним, F- критерій більший за табличний (11,37>4,76), що свідчить про те, що модель відповідає реальній дійсності, t-критерій більший за табличний (3,58>2,45), що свідчить про значимість коефіцієнта кореляції; для Y2 коефіцієнт детермінації = 0,912, що свідчить про те, що 0,912 частина варіації залежної змінної пояснена моделлю, коефіцієнт кореляції = 0,955 показує, що вплив змінної X на Y є сильним, F- критерій менший за табличний (0,22<4,76), що свідчить про те, що модель не відповідає реальній дійсності, t-критерій більший за табличний (8,50>2,45), що свідчить про значимість коефіцієнта кореляції. Проаналізуємо систему у приведеній формі, рівноважна кількість споживання продуктів майже не залежить від доходу на душу населення та буде збільшуватися при підвищенні витрат на виробництво одиниці продукції. Ціна одиниці продукції буде збільшуватися при підвищенні доходу на душу населення та зменшенні витрат на виробництво одиниці продукції. Аналізуючи стандартні помилки відносно абсолютного значення в обох моделях , можна сказати , що побудовані моделі методом 1МНК є недійсними. Адже дані значення мають дуже велику різницю між собою та даними задачі. Це можна пояснити високими значеннями дисперсії залишків. А так як, дані системи ідентифіковані, ми не можемо використовувати інший метод. Розраховані прогнозні значення ендогенних змінних моделі на основі системи рівнянь показали, що: При ціні одиниці продукції 50 грн. та доході на душу населення 90 грн. будемо мати рівноважну кількість споживання продуктів 24,64 тис. грн. При ціні одиниці продукції 48 грн. та доході на душу населення 150 грн. будемо мати рівноважну кількість споживання продуктів 23,26 тис. грн. При рівноважній кількості споживання продуктів 65 тис. грн. та витратах в середньому на виробництво одиниці продукції 53 грн. будемо мати ціну одиниці продукції 76,33 грн. При рівноважній кількості споживання продуктів 62 тис. грн. та витратах в середньому на виробництво одиниці продукції 44 грн. будемо мати ціну одиниці продукції 49,25 грн. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
