Подбор оптимального значения альфа
Задание 3. В таблице задан поквартальный объем продаж автомобилей фирмой.
Порядковый номер квартала t
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
Объем продаж шт.
|
235
|
234
|
227
|
222
|
218
|
199
|
197
|
203
|
208
|
|
Порядковый номер квартала t
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
|
Объем продаж шт.
|
212
|
217
|
232
|
230
|
220
|
213
|
218
|
219
|
215
|
Выполнить экспоненциальное сглаживание при значении α=0,1, α=0,5, α=0,9.
Сравнить графически исходный временной ряд и экспоненциально сглаженные временные ряды.
Выбрать лучшее значение α.
Спрогнозировать объем продаж на 19 кв.
Решение
Порядковый номер квартала
|
Объем продаж
|
α=0,1
|
|
α=0,5
|
|
α=0,9
|
|
1
|
235
|
прогноз
|
|
прогноз
|
|
прогноз
|
|
2
|
234
|
235
|
|
235
|
|
235
|
|
3
|
227
|
234,1
|
|
234,5
|
|
234,9
|
|
4
|
222
|
227,71
|
ошибка
|
230,75
|
ошибка
|
234,11
|
ошибка
|
5
|
218
|
222,571
|
5,291947
|
226,375
|
6,678635
|
232,899
|
8,367837
|
6
|
199
|
218,4571
|
5,88524
|
222,1875
|
8,225025
|
231,4091
|
11,98669
|
7
|
197
|
200,9457
|
12,00107
|
210,5938
|
15,10368
|
228,1682
|
21,74843
|
8
|
203
|
197,3946
|
11,76211
|
203,7969
|
16,25414
|
225,0514
|
27,34828
|
9
|
208
|
202,4395
|
11,91033
|
203,3984
|
15,52509
|
222,8462
|
28,91406
|
10
|
212
|
207,4439
|
5,096047
|
205,6992
|
8,298583
|
221,3616
|
23,65114
|
11
|
217
|
211,5444
|
5,263019
|
208,8496
|
4,528032
|
220,4254
|
16,27179
|
12
|
232
|
216,4544
|
5,210275
|
212,9248
|
6,514166
|
220,0829
|
10,32447
|
13
|
230
|
231,8445
|
9,554139
|
227,2312
|
13,18152
|
222,3472
|
9,46546
|
14
|
220
|
230,1845
|
9,082647
|
228,6156
|
12,41632
|
223,1124
|
10,25698
|
15
|
213
|
221,0184
|
6,042684
|
224,3078
|
7,590797
|
222,8012
|
7,816377
|
16
|
218
|
213,8018
|
7,559121
|
218,6539
|
8,361841
|
221,8211
|
7,400827
|
17
|
219
|
217,5802
|
7,86645
|
218,327
|
8,216295
|
221,439
|
6,333805
|
18
|
215
|
218,858
|
5,289482
|
218,6635
|
6,551003
|
221,1951
|
6,23465
|
19
|
|
218,47
|
|
216,8317
|
|
215,61
|
|
20
|
|
|
|
|
|
|
|
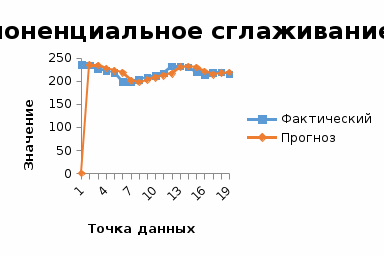
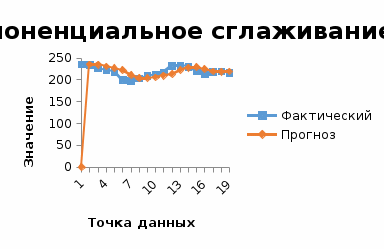
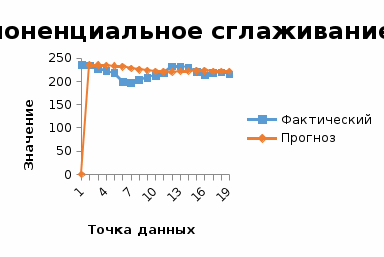
Для выбора лучшей модели оценим корень из средней квадратичной ошибки прогноза
Альфа
|
0,1
|
|
|
Альфа
|
|
0,5
|
Альфа
|
|
0,9
|
СрОшибка
|
8,028141
|
|
|
СрОшибка
|
|
9,997445
|
СрОшибка
|
|
13,67273
|
СТДОтклОшибки
|
2,661369
|
|
|
СТДОтклОшибки
|
|
3,786416
|
СТДОтклОшибки
|
|
7,871088
|
КСКОП
|
8,457774
|
|
|
КСКОП
|
|
10,69046
|
КСКОП
|
|
15,77649
|
альфа
|
КСКОП
|
|
|
|
|
|
|
|
|
|
0,1
|
8,45
|
|
|
|
|
|
|
|
|
|
0,5
|
10,69
|
|
|
|
|
|
|
|
|
|
0,9
|
15,78
|
|
|
|
|
|
|
|
|
|
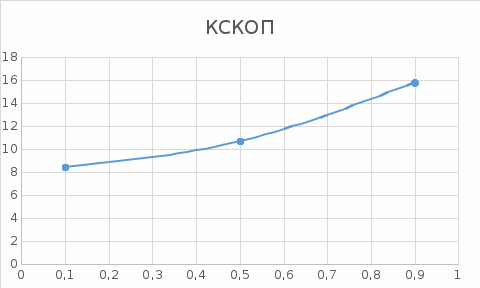
Лучшей моделью считается та, у которой минимальный КСКОП
Следовательно, лучшей константой для данного случая является α= 0,1
Прогноз на 19 квартал = 218,47 тыс.руб.
Формулы:
КСКОП=КОРЕНЬ(СрОшибка2 + СТДОтклОшибка2)
СрОшибка=СРЗНАЧ(Ошибка)
СТДОтклОшибки=СТАНДОТКЛОН.В(Ошибка)
Ошибка – диапазон ячеек ошибки
Прогноз
У t+1=Yt+(1-)St |
 Скачать 32.79 Kb.
Скачать 32.79 Kb.



