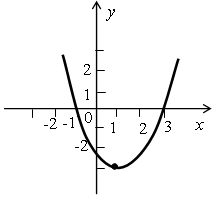Построение графика квадратичной функции
 Скачать 58.86 Kb. Скачать 58.86 Kb.
|
|
Урок № 23 Дата: Класс: Тема: Построение графика квадратичной функции Цели: продолжить формирование умения строить график квадратичной функции и перечислять ее свойства; выявить влияние коэффициентов а, b и с на расположение графика квадратичной функции. Планируемые результаты: Предметные: уметь строить графики квадратичной функции, заданной формулой. Личностные: осознание математической составляющей окружающего мира. Регулятивные: осознание возникшей проблемы, определение последовательности и составление плана и последовательности действий для решения возникшей проблемы, внесение необходимых дополнений и коррективов в план и способ действий в случае расхождения эталона. Реального действия и его результата с учётом оценки этого результата самими обучающимся, учителем, товарищами. Познавательные: моделирование ситуации из жизни, постановка и формулирование проблемы, самостоятельное создание алгоритмов деятельности при решении проблем творческого и поискового характера, выбор наиболее эффективных способов решения задач в зависимости от конкретных условий, рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности. Коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации; владение монологической и диалогической формами речи, умение работать индивидуально и в парах. Тип урока: урок изучения материала. Оборудование: интерактивная доска, ноутбук, презентация. Ход урока I. Организационный момент. II. Устная работа. Определите, график какой функции изображен на рисунке:
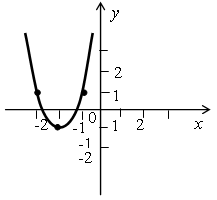
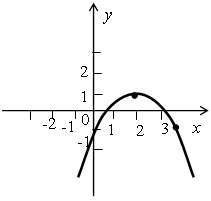
III. Формирование умений и навыков. Упражнения: 1. № 127 (а). 2. № 129. Р е ш е н и е Прямая у = 6х + b касается параболы у = х2 + 8, то есть имеет с ней только одну общую точку в том случае, когда уравнение 6х + b = х2 + 8 будет иметь единственное решение. Это уравнение является квадратным, найдем его дискриминант: х2 – 6х + 8 + b = 0; D1 = 9 – (8 – b) = 1 + b; D1 = 0, если 1 + b = 0, то есть b = –1. О т в е т: b = –1. 3. Выявить влияние коэффициентов а, b и с на расположение графика функции у = ах2 + bх + с. Учащиеся обладают достаточными знаниями, чтобы выполнить это задание самостоятельно. Следует предложить им все полученные выводы занести в тетрадь, при этом выделив «основную» роль каждого из коэффициентов. 1) Коэффициент а влияет на направление ветвей параболы: при а > 0 – ветви направлены вверх, при а < 0 – вниз. 2) Коэффициент b влияет на расположение вершины параболы. При b = 0 вершина лежит на оси оу. 3) Коэффициент с показывает точку пересечения параболы с осью ОУ. После этого можно привести пример, показывающий, что можно сказать о коэффициентах а, b и с по графику функции.  Значение с можно назвать точно: поскольку график пересекает ось ОУ в точке (0; 1), то с = 1. Коэффициент а можно сравнить с нулем: так как ветви параболы направлены вниз, то а < 0. Знак коэффициента b можно узнать из формулы, определяющей абсциссу вершины параболы: т = 4. Определите, график какой функции изображен на рисунке, опираясь на значение коэффициентов а, b и с.
Р е ш е н и е По изображенному графику делаем следующие выводы о коэффициентах а, b и с: а > 0, так как ветви параболы направлены вверх; b ≠ 0, так как вершина параболы не лежит на оси ОУ; с = –2, так как парабола пересекает ось ординат в точке (0; –2). Всем этим условиям удовлетворяет только функция у = 2х2 – 3х – 2.
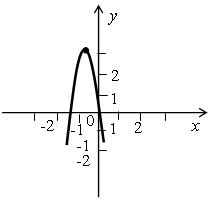
Р е ш е н и е По изображенному графику делаем следующие выводы о коэффициентах а, b и с: а < 0, так как ветви параболы направлены вниз; b ≠ 0, так как вершина параболы не лежит на оси ОУ; с = 0, так как парабола пересекает ось ОУ в точке (0; 0). Всем этим условиям удовлетворяет только функция у = –2,7х2 – 2х. 5. По графику функции у = ах2 + bх + с определите знаки коэффициентов а, b и с: а) 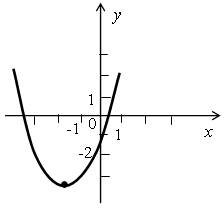 б) б) 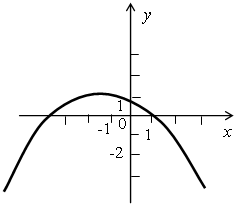 Р е ш е н и е а) Ветви параболы направлены вверх, поэтому а > 0. Парабола пересекает ось ординат в нижней полуплоскости, поэтому с < 0. Чтобы узнать знак коэффициента b воспользуемся формулой для нахождения абсциссы вершины параболы: т = б) Аналогично определяем знаки коэффициентов а, b и с: а < 0, с > 0, b < 0. Сильным в учебе учащимся можно дать дополнительно выполнить № 247. Р е ш е н и е у = х2 + рх + q. а) По теореме Виета, известно, что если х1 и х2 – корни уравнения х2 + + рх + q = 0 (то есть нули данной функции), то х1 · х2 = q и х1 + х2 = –р. Получаем, что q = 3 · 4 = 12 и р = –(3 + 4) = –7. б) Точка пересечения параболы с осью ОУ даст значение параметра q, то есть q = 6. Если график функции пересекает ось ОХ в точке (2; 0), то число 2 является корнем уравнения х2 + рх + q = 0. Подставляя значение х = 2 в это уравнение, получим, что р = –5. в) Своего наименьшего значения данная квадратичная функция достигает в вершине параболы, поэтому IV. Проверочная работа. В а р и а н т 1 1. Постройте график функции у = 2х2 + 4х – 6 и найдите, используя график: а) нули функции; б) промежутки, в которых у > 0 и y < 0; в) промежутки возрастания и убывания функции; г) наименьшее значение функции; д) область значения функции. 2. Не строя график функции у = –х2 + 4х, найдите: а) нули функции; б) промежутки возрастания и убывания функции; в) область значения функции. 3. По графику функции у = ах2 + bх + с определите знаки коэффициентов а, b и с: 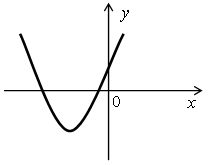 В а р и а н т 2 1. Постройте график функции у = –х2 + 2х + 3 и найдите, используя график: а) нули функции; б) промежутки, в которых у > 0 и y < 0; в) промежутки возрастания и убывания функции; г) наибольшее значение функции; д) область значения функции. 2. Не строя график функции у = 2х2 + 8х, найдите: а) нули функции; б) промежутки возрастания и убывания функции; в) область значения функции. 3. По графику функции у = ах2 + bх + с определите знаки коэффициентов а, b и с:  V. Итоги урока. В о п р о с ы у ч а щ и м с я: – Опишите алгоритм построения квадратичной функции. – Перечислите свойства функции у = ах2 + bх + с при а > 0 и при а < 0. – Как влияют коэффициенты а, b и с на расположение графика квадратичной функции? Домашнее задание: № 127 (б), № 128, № 248. Д о п о л н и т е л ь н о: № 130. |