Материал. Подъем жидкостей в капиллярах
 Скачать 133.42 Kb. Скачать 133.42 Kb.
|
|
Неоднородность свойств горных пород, методы ее изучения и отображения. Использование полученных данных при проектирования разработки газовых и газоконденсатных месторождений. Неоднородность горных пород по проницаемости и способы ее определения. Статистические методы ее отображения. Учет неоднородности при выборе системы разработки, вскрытии неоднородных пластов в соответствии с запасами флюидов и характеристиками пористой среды. Подъем жидкостей в капиллярах. Рассмотрим капиллярную трубку очень малого диаметра. Если такую трубку одним концом опустить в сосуд со свободным уровнем жидкости, то жидкость будет подниматься в трубке выше ее свободного уровня в сосуде. Эта разница уровней возникает вследствие действия сил взаимодействия (адгезионного натяжения) между внутренней стенкой трубки и жидкостью, которые преодолевают вес столба жидкости в трубке. Вследствие адгезионного натяжения жидкость стремится прилипнуть к внутренней поверхности трубки и будет подниматься в ней до тех пор, пока равнодействующая сил, действующих на жидкость вверх, не уравновесится весом столба жидкости, находящейся в трубке (рис 9). Давление в жидкой фазе в капилляре под границей раздела газ – жидкость меньше, чем давление в газовой фазе над этой границей. Разница давлений по обе стороны границы раздела называется капиллярным давлением системы рк. Из приравнивания сил веса жидкости и подъёмной на поверхности раздела в капилляре получим выражение для определения капиллярного давления, как функции поверхностных сил 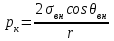 . . Из данного соотношения видно, что к увеличению высоты подъёма воды в капилляре приводит уменьшение радиуса капилляра и уменьшение угла смачивания . Последнее объясняет образование языков заводнения через наименее проницаемые коллектора. Для изучения угла смачивания поверхности твердых тел и смачивающих свойств жидкостей пользуются оптической скамьей. При этом каплю, жидкости нанесенную на твердую поверхность минерала проектируют с помощью оптической системы в увеличенном виде на экран, и краевой угол смачивания измеряют по изображению. 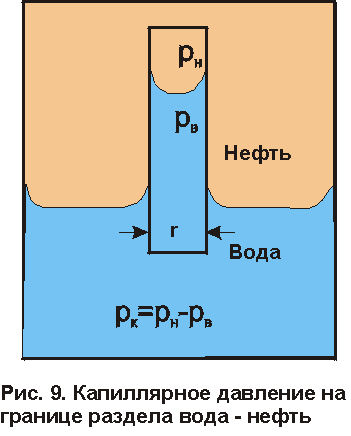 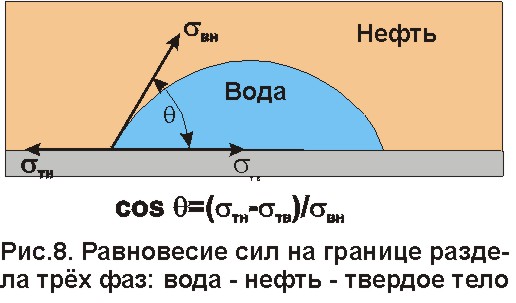 Экспериментальные данные по распределению пор позволяют построить кривые капиллярное давление-водонасыщенность пор жидкостью. Типичный вид такой кривой для пород различной проницаемости приведен на рис. 11. По оси абсцисс откладывается водонасыщенность породы (в долях единицы или в процентах), а по оси ординат - капиллярное давление рК, соответствующее данной водонасыщенности Sn. Считается, что метод полупроницаемых перегородок позволяет получить зависимости pK-SB> наиболее близкие к пластовым условиям, в связи с возможностью использования в опытах воды и нефти в качестве первоначально насыщающей образец фазы и вытесняющей среды. По смачивающим и другим свойствам модельная система приближается к пластовой. Зависимости pK-SB широко используют при оценке остаточной водонасыщенности пород для изучения строения переходных зон нефть-вода, вода-газ. Как следует из рис. 11, характер зависимости рк = f(SВ) в значительной степени определяется проницаемостью пористых сред. Очевидно, другие свойства пород, а также параметры жидкостей влияют на форму кривых рк = f(SВ). Левереттом была впервые сделана попытка учесть влияние свойств пород и жидкостей и свести данные о зависимости капиллярного давления от насыщенности различных пластов в единую зависимость с помощью функции 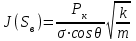 По формулам (1.19) и (1.22) легко установить, что функция Леверетта представляет собой отношение капиллярного давления Рк, соответствующего различной степени насыщенности пор, к величине, пропорциональной среднему значению капиллярного давления, развиваемого менисками в порах со средним радиусом. Однако анализ показал, что предположение о вероятном совпадении зависимостей функция Леверетта J , водонасыщенность SB для всех пород на практике не оправдалось. На для примера приведены зависимости J =f(SB), полученные Н.С. Гудок, для различных пород продуктивных пластов нижнего мела Прикумской нефтеносной области. Для корреляции зависимостей J =f(SB), полученных для различных пород, применяются также статистические методы. Фазовая проницаемость при многофазном насыщении пласта Рассмотрим двухфазный поток несмешивающихся флюидов. Пусть в пласт нагнетаются две фазы. Начальное - природное распределение флюидов соответствует распределению, показанному на рис. 3.3.3 г. Если течение очень медленное, а приложенный градиент давления не будет деформировать межфазные поверхности раздела, то распределение флюидов в пласте будет полностью определяться капиллярными силами. Каждый флюид будет протекать по своей собственной системе сообщающихся пор (см. рис. 3.3.3 г). Так как флюиды текут по своим поровым сетям, то определяющим отличием от однофазной фильтрации является неполнота участия отдельных капилляров и пор в процессе фильтрации. Так как часть поровой системы занята другой фазой, то объемный поток каждой из фаз меньше, чем если бы он был для одной фазы, движущейся при том же перепаде давления. Последнее аналогично падению проницаемости для исследуемой фазы. Маскет (1936) обобщил закон Дарси на случай многофазной фильтрации 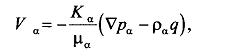 где Ka - некая новая проницаемость фильтрующейся фазы а в присутствии других фаз; μа - вязкость; ∆pa - градиент давления; ρа - плотность фазы a; V а скорость фильтрации фазы а. Проницаемость при многофазной фильтрации Ка оказалась зависящей от значений абсолютной проницаемости (К0), степени насыщения порового пространства фазой а и от структуры порового пространства. Значения абсолютной проницаемости для нефтегазовых пластов меняются в широком диапазоне. При двухфазной фильтрации степень насыщения пор фильтрующимися фазами также сильно меняется. Пласты-коллекторы характеризуются непостоянством структуры порового пространства. Соответственно проницаемость Ка при совместной фильтрации фаз становится крайне неопределенной из-за изменчивости фильтрационных, микроструктурных характеристик пласта и степени его насыщения фильтрующейся фазой. Для удобства практического использования была введена безразмерная прони- цаемость Кr,а= 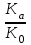 , где Кr,а и К0 - значения фазовой проницаемости для фазы а в Ко , где Кr,а и К0 - значения фазовой проницаемости для фазы а в Коприсутствии других фаз и значения абсолютной проницаемости. Безразмерная проницаемость Кr,а гораздо менее чувствительна к микроструктурным изменениям пласта и зависит в основном от степени насыщения пласта фильтрующимися фазами. Безразмерная проницаемость Кr,а получила название относительной фазовой проницаемости (ОФП). Физический смысл относительной фазовой проницаемости - это относительное уменьшение проницаемости по фазе а по отношению к абсолютной, обусловленное присутствием других фаз. Относительная проницаемость является функцией насыщенности, так как если фаза занимает большую часть объема, то она может течь через большую площадь потока. В промысловой практике ОФП часто нормируется не по абсолютной проницаемости, а по фазовой проницаемости для одной из фильтрующихся фаз (Кф ). В этом случае относительная фазовая проницаемость определяется следующим образом Нормировка по фазовой проницаемости КФ1 удобна в практическом смысле, однако создает дополнительные неопределенности, связанные с влиянием компонентного состава фильтрующейся фазы и физических полей на величину фазовой проницаемости Кф!. Исходя из физического смысла относительной фазовой проницаемости, ясно, что эта проницаемость определяется не только структурой порового пространства, которая полностью контролирует абсолютную проницаемость (см. разд. 3.2). Относительная же фазовая проницаемость кроме структуры порового пространства зависит также и от других параметров, характеризующих пластовую систему: скелет пласта - флюид 1 - флюид 2 в процессе двухфазной фильтрации. К таким параметрам относятся смачиваемость, соотношение капиллярных и напорных (гидродинамических) сил, соотношение вязкостей вытесняющего и вытесняемого флюидов, действие внешних физических полей и др. Используя понятие относительной фазовой проницаемости по г-й фазе Kri, можно записать обобщенный закон Дарси в виде 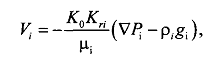 где Vi - скорость фильтрации i-й фазы; μi;, рi, Рi, - вязкость, плотность и давление в i'-й фазе. Обобщенный закон Дарси в форме предполагает использование в качестве постоянных величин для каждого флюида следующие параметры: Vi Pi К0 Kri, ρi, μi,-. Это означает, что нефтегазовый пласт рассматривается состоящим из серии блоков, размеры которых достаточно малы, чтобы считать значения вышеназванных параметров приближенно постоянными. С другой стороны, размеры блоков достаточно велики, чтобы считать применимым закон Дарси в макроскопическом виде для каждого отдельного блока. Давления в фильтрующихся фазах (Р,) определяются, исходя из гипотезы о том, что давления Р, в любых двух фазах связаны друг с другом посредством капиллярного давления Рк. Следовательно, два градиента давления в соотношениях (3.3.4) и связаны друг с другом через градиент капиллярного давления ∆P2-∆P1=∆Pk Последнее соотношение является замыкающим в обобщенном законе Дарси. Поскольку относительная фазовая проницаемость (Кг,а) зависит от ряда параметров, характеризующих систему скелет пласта - вытесняющий флюид - вытесняемый флюид, то в общем случае эта система в процессе стационарной однонаправленной фильтрации может быть определена следующими безразмерными параметрами 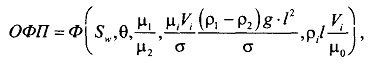 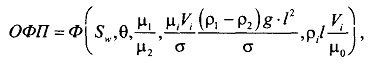 где / - характерный размер пор, Sw - насыщенность смачивающей фазой, μ- вязкость i-й фазы; Vi - скорость фильтрации i-й фазы, ρi, - плотность i-й фазы, σ - поверхностное натяжение на границах раздела фаз, € - краевой угол смачивания. Относительные фазовые проницаемости в общем случае могут зависеть от всех безразмерных параметров из соотношения (3.3.7). Однако существует целый ряд типичных геолого-технологических условий, при которых ОФП определяются лишь одним или двумя параметрами из набора . Абсолютная проницаемость Проницаемость, определенная при фильтрации «инертных» флюидов и при полном насыщении пласта этими флюидами (абсолютная проницаемость) является физической абстракцией типа идеального газа, абсолютно твердого тела или идеальной жидкости. Тем не менее исследование именно абсолютной проницаемости является базовым при анализе влияния свойств пласта на движение в нем жидкостей и газов. Благодаря наличию абсолютной проницаемости появляются возможности стандартизации условий проведения лабораторных экспериментов, сравнительного анализа и классификации пород по фильтрационной способности. Абсолютная проницаемость является важной составной частью фазовой и относительной фазовой проницаемости. Измерение проницаемости для изотропной среды проводится в лабораторных условиях на линейных образцах керна цилиндрической формы. Согласно существующему стандарту эксперименты проводятся на хорошо отмытых и экстрагированных от пластовых углеводородов, хорошо просушенных образцах керна. В экспериментах моделируются пластовые условия - давление и температура. Для избежания ошибок эксперименты проводятся при различных скоростях течения. Это позволяет проверить выполнение линейного закона Дарси и удостовериться, что зависимость 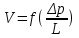 прямо пропорциональна и проходит через начало координат. В противном случае закон Дарси не выполняется. В качестве инертного флюида обычно используется газ, и проницаемость определяется для газа. прямо пропорциональна и проходит через начало координат. В противном случае закон Дарси не выполняется. В качестве инертного флюида обычно используется газ, и проницаемость определяется для газа.Теоретические модели абсолютной проницаемости Для абсолютной проницаемости возможен теоретический анализ зависимости проницаемости от особенностей микроструктуры пласта. Влияние микростроения пласта на проницаемость обычно рассматривается для двух основных типов структурных моделей: гранулярных моделей (фиктивный грунт) и капиллярных моделей (идеальный грунт) (см. разд. 2.8.5). Гранулярные модели представляют пласт в виде различным образом упакованных частиц (гранул). В капиллярных моделях пористая среда представляется совокупностью систем капиллярных трубок, которые могут различаться по форме, размерам и ориентации (см. разд. 2.8). Для низкопроницаемых сцементированных пород со средней пористостью капиллярные модели являются более адекватными проницаемости реальных пластов. Для высокопористых слабосцементированных пород предпочтение отдается гранулярным моделям. Реальные пласты не могут быть достаточно полно описаны ни одним из этих типов моделей. Тем не менее даже упрощенное представление о пустотном пространстве пласта позволяет полнее понять механизмы влияния поровой структуры пустот на проницаемость и получить важные с практической точки зрения корреляции между проницаемостью и другими свойствами пласта. При определении проницаемости в структурных моделях используется феноменологический подход, базирующийся на аналогии течения вязкой, несжимаемой, однородной жидкости в трубах и движения жидкости в поровом пространстве (гидравлическая аналогия). При этом задаются конкретным видом выражений для числа Рейнольдса (Re) и коэффициента гидравлического сопротивления (к) и принимают, что линеиная зависимость между этими параметрами задается формулой 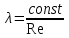 которая справедлива для ламинарного течения в трубах. Для пород-коллекторов подобное представление справедливо лишь для определенного диапазона чисел Рейнольдса и именно в этом диапазоне чисел Рейнольдса справедливы все дальнейшие теоретические построения. Модели гранулярной проницаемости определяют коэффициент гидравлического сопротивления и число Рейнольдса в виде 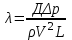 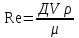 где Д - некоторый эффективный диаметр частицы (гранулы); р - плотность флюида; ∆р - перепад давления на длине L; V - средняя скорость движения жидкости в порах, μ - вязкость. Для моделей пласта, представленных частицами произвольной формы и характеризующихся определенным законом распределения частиц по размеру, согласно имеющимся исследованиям (Rumpf and Gupte, 1971) существует функциональная зависимость между следующими безразмерными параметрами. Анализ экспериментальных данных показал, что в диапазоне чисел Рейнольдса 10-1 < Re < 102 имеется четкая зависимость коэффициента гидравлического сопротивления, умноженного на некоторую функцию пористости , от числа Рейнольдса (Re) 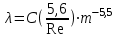 Из сравнения соотношения (3.1.5) с законом Дарси получаем выражение для коэффициента проницаемости 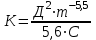 Последнее соотношение показывает, что в гранулярной модели проницаемость прямо пропорциональна квадрату эффективного диаметра частиц умноженному на некоторую функцию пористости . Модели капиллярной проницаемости в отличие от гранулярных моделей основаны на представлении поровой структуры в виде пучка капилляров с жесткими стенками, которые могут отличаться как размерами, так и ориентацией в пространстве. В гранулярной проницаемости форма, сечение и длина капилляров определяются формой, размерами и взаимным расположением частиц. В капиллярных моделях параметры поровой структуры являются независимыми характеристиками скелета пласта (см. разд. 2.8.5). Существуют два типа капиллярных моделей. Первый, основанный на сильном допущении о том, что поровая структура реального неоднородного по размерам, форме и конфигурации пор пласта может быть заменена одним капилляром со средним гидравлическим радиусом. Другой подход предусматривает использование системы капилляров с непосредственной связью между радиусом капилляров в пучке, с пористостью и проницаемостью. В основе капиллярных моделей лежат идеи течения жидкости в каналах правильной формы, без учета эффектов гидродинамического взаимодействия отдельных пор друг с другом. Все капиллярные модели, которые рассматриваются далее, являются одномерными, что является существенным упрощением реальности и в этом смысле пористость модели равна ее просветности, а движение жидкости по капиллярам происходит только в одном направлении. Модель среднего гидравлического радиуса (модель Козени-Кармана) В теории Козени-Кармана (Kozeny, 1927, Karman, 1937, 1938, 1956), которую часто называют теорией гидравлического радиуса. Считается, что реальная пористая среда эквивалентна одному капилляру, поперечное сечение которого имеет крайне сложную, но в среднем постоянную форму. 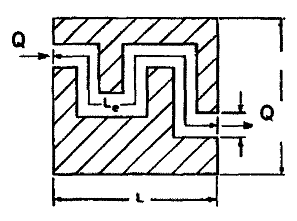 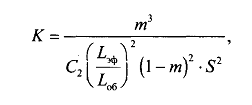 Где величина 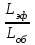 обычно называется гидравлической извилистостью или коэффициентом извилистости; величина обычно называется гидравлической извилистостью или коэффициентом извилистости; величина 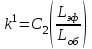 называется числом Кармана; S=Sk/Vck называется числом Кармана; S=Sk/VckЭкспериментальная проверка уравнения Козени-Кармана была проведена для различных неконсолидированных пористых сред. При узком распределении частиц по размерам уравнение (3.1.12) дает хорошее совпадение между результатами расчетов и экспериментом. Уравнение Козени-Кармана хорошо описывает связь между пористостью, проницаемостью и удельной поверхностью для несцементированных пород. Исследования Кармана показали, что уравнение (3.1.12) для уплотненных сцементированных пород хорошо описывает и результаты проведенных экспериментов лишь в случае значений числа Кармана равно 5. Исследования Wyllie (1955) установили адекватность уравнения Козени-Кармана и при значениях числа Кармана, существенно превышающего значение 5. Проницаемость в моделях пучка капилляров моделируется системой параллельных капиллярных трубок заданной геометрии. Трубки могут быть одного размера; однородными по геометрии, но разного размера (распределение трубок по размеру по аналогии с органом); могут быть периодически сужающиеся трубки одного размера, могут быть и периодически сужающимися и разного размера. Все эти модельные системы позволяют определить проницаемость и исследовать влияние поровой структуры на проницаемость. Haring и Green Korn (1970) предложили статистическую модель проницаемости, состоящую из большого числа произвольно ориентированных цилиндрических капилляров. В модели использовано 4 независимых переменных: длина капилляров, его радиус R и два угла 0 и ф, определяющие ориентацию поры в трехмерном пространстве. 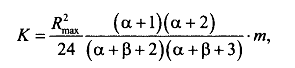 где α β- параметры бета-функции, определяемые из экспериментальных данных по распределению пор по размерам. Проницаемость коллекторов в процессе разработки месторождений Значительно более подвержена изменению проницаемость горных пород. Если считать, что коэффициент пористости изменяется лишь вследствие уменьшения в увеличения объема пор породы, зависимость упругих изменений проницаемости для плотных пород от давления можно выразить соотношением 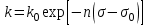 , 17 , 17где 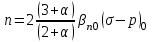 ; -коэффициент, характеризующий структуру поровых каналов. ; -коэффициент, характеризующий структуру поровых каналов.Для сцементированных песчаников находится в интервале -1,25+ -1,8. По результатам исследований, коэффициент, проницаемости при упругом деформировании, например песчано-глинистых пород, залегающих на глубине 1300-2000м может уменьшаться по сравнению с данными, полученными при атмосферных условиях, на 10—40%. Как уже упоминалось, деформации горных пород могут сопровождаться пластическими явлениями. При этом порода при снятии с нее напряжений не восстанавливает свою геометрию, изменяются вследствие остаточных деформаций пористость и проницаемость. |
