сор 2 геометрия с решением. Г8 СОр2 1вар с решением. Подготовка суммативное оценивание по геометрии за раздел соотношения между сторонами и углами прямоугольного треугольника 8 класс сор2 задания
 Скачать 36.64 Kb. Скачать 36.64 Kb.
|
|
Подготовка: СУММАТИВНОЕ ОЦЕНИВАНИЕ по геометрии ЗА РАЗДЕЛ «СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА» 8 класс сор2 ЗАДАНИЯ
ВАРИАНТ 1 1.Используя данные рисунка, найдите синус, косинус, тангенс и котангенс угла А треугольника АВС с прямым углом С. 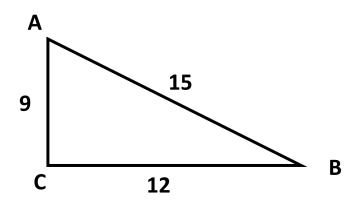 Решение: 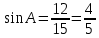 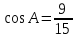 = =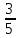 tg = tg = 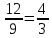 ctg = ctg = 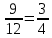 2.Найдите гипотенузу прямоугольного треугольника, если катеты соответственно равны 8 см и 11 см. Найдём по теореме Пифагора с²=а²+b² c²=8²+11² c²=64+121=185 c 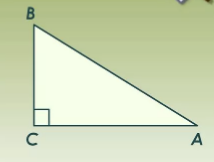 =√185≈13,6 =√185≈13,63.Найдите значение 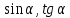 и и 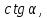 если если 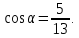 Sin2α + cos 2 α = 1 sinα = √ (1 - 25/169) = √ (144/169) = 12/13 tgα = 12/13 : 5/13 = 12/5 ctgα = 5/13: 12/13 = 5/12 4.Архитектурное сооружение монумент «Байтерек» считается символом обновления Казахстана. Оно представляет собой высокую металлическую конструкцию с огромным позолоченным стеклянным шаром на вершине. Высота монумента составляет 97 м, а с шаром, венчающим конструкцию - 105 м. Монумент виден из точки А на поверхности земли, под углом 60°. Найдите расстояние от точки А до основания монумента и до его самой высокой точки. Дано: 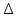 АВС, А=60°, С=90°, ВС=105 м. АВС, А=60°, С=90°, ВС=105 м. Найти: АС , АВ. Решение: 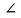 В=90-60=30°, значит АВ=2АС по свойству катета, лежащего против угла 30° В=90-60=30°, значит АВ=2АС по свойству катета, лежащего против угла 30°П  о теореме Пифагора АВ²=ВС²+АС² о теореме Пифагора АВ²=ВС²+АС²(2х)²=105²+х²; 4х²-х²=11025; 3х²=11025; х²=3675; х≈60,62 м. АС≈60,62 м, АВ=60,62*2≈121,24 м. Ответ: АС≈60,62 м, АВ≈121,24 м. | ||||||||||||||||||||
