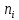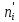ОТН-контрольная работа-2022 ЗФО. Подпись, дата контрольная работа по дисциплине Основы теории надежности Оценка и анализ надежности планера, систем, силовой установки и оборудования воздушного судна Вариант Шифр кр Контрольную
 Скачать 255.52 Kb. Скачать 255.52 Kb.
|
 ФЕДЕРАЛЬНОЕ АГЕНТСТВО ВОЗДУШНОГО ТРАНСПОРТА ИРКУТСКИЙ ФИЛИАЛ ФЕДЕРАЛЬНОГО ГОСУДАРСТВЕННОГО БЮДЖЕТНОГО ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ ВЫСШЕГО ОБРАЗОВАНИЯ «МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ГРАЖДАНСКОЙ АВИАЦИИ» (МГТУ ГА) Кафедра Летательных аппаратов и двигателей Защищена с оценкой _________ _____________________ (подпись, дата) КОНТРОЛЬНАЯ РАБОТА ПО ДИСЦИПЛИНЕ «Основы теории надежности» Оценка и анализ надежности планера, систем, силовой установки и оборудования воздушного судна Вариант ___ Шифр КР:___________ Контрольную работу выполнил студент_____________________ ____________________________ (фамилия, имя, отчество) Группа______________________ ____________________________ (подпись, дата) Иркутск 2022 г ФЕДЕРАЛЬНОЕ АГЕНТСТВО ВОЗДУШНОГО ТРАНСПОРТА ИРКУТСКИЙ ФИЛИАЛ ФЕДЕРАЛЬНОГО ГОСУДАРСТВЕННОГО БЮДЖЕТНОГО ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯВЫСШЕГО ОБРАЗОВАНИЯ «МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ГРАЖДАНСКОЙ АВИАЦИИ» (МГТУ ГА) Кафедра Летательных аппаратов и двигателей ТЕХНИЧЕСКОЕ ЗАДАНИЕ на контрольную работу по дисциплине «Основы теории надежности» Студенту __________________________________, группа_______ Вариант задания, выдаваемый преподавателем _____ Дата выдачи технического задания _______________________________ Руководитель__________________________________________________ Студент_______________________________________________________ Рекомендованная литература: 1. Ицкович А.А., Файнбург И.А. Основы теории надежности. Пособие по изучению дисциплины и выполнению курсовой работы. – М.: МГТУ ГА, 2015. – 68 с. 2. Чокой В.З. Основы теории надежности. Учебное пособие. – Иркутск: Иркутский филиал МГТУ ГА, 2019 – 81 с. 3. Чокой В.З. Оценка, анализ и прогнозирование процессов в авиатранспортных системах. Расчетно-аналитический модуль EDUCATOR версия 1.1. Электронный ресурс. – Иркутск: Иркутский филиал МГТУ ГА, 2020. – 748 МБ. СОДЕРЖАНИЕ Задание 1 –Подбор нормального распределения для результатов наблюдений…………..3 Задание 2 – Оценка параметров теоретических распределений..………………………….7 Задание 3 – Параметрическая оценка безотказности воздушного судна…………………..9 Список использованных источников…………………………………………………………17 Приложение А. Справочные таблицы………………………………………………………..18 Приложение Б. Варианты исходных данных………………………………………………..21 Задание 1 – Подбор нормального распределения для результатов наблюдений Текст задания и исходные данные. В ходе наблюдений за состоянием смазки в подшипниках колес шасси в 70 случаях была зафиксирована внеплановая необходимость замены смазки. В частности при календарном сроке 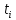 (в неделях): 2,5; 3,0; 3,5; 4,0; 4,5; 4,5; 5,0; 5,5; 6,0; 6,0; 6,5; 6,5; 7,0; 7,5; 8,0; 8,5; 8,5; 8,5; 9,0; 9,0; 9,0; 9,0; 9,5; 10,0; 10,0; 10,5; 10,5; 11,0; 11,0; 11,5; 11,5; 11,5; 11,5; 12,0; 12,0; 12,0; 12,0; 12,0; 12,0; 12,0; 12,5; 13,0; 13,0; 13,0; 13,0; 13,0; 13,0; 13,0; 13,5; 13,5; 14,0; 14,5; 14,5; 14,5; 14,5; 15,0; 15,0; 15,0; 15,0; 15,0; 15,5; 16,0; 16,0; 17,0; 17,0; 17,5; 17,5; 18,0; 19,0; 20,0 ( (в неделях): 2,5; 3,0; 3,5; 4,0; 4,5; 4,5; 5,0; 5,5; 6,0; 6,0; 6,5; 6,5; 7,0; 7,5; 8,0; 8,5; 8,5; 8,5; 9,0; 9,0; 9,0; 9,0; 9,5; 10,0; 10,0; 10,5; 10,5; 11,0; 11,0; 11,5; 11,5; 11,5; 11,5; 12,0; 12,0; 12,0; 12,0; 12,0; 12,0; 12,0; 12,5; 13,0; 13,0; 13,0; 13,0; 13,0; 13,0; 13,0; 13,5; 13,5; 14,0; 14,5; 14,5; 14,5; 14,5; 15,0; 15,0; 15,0; 15,0; 15,0; 15,5; 16,0; 16,0; 17,0; 17,0; 17,5; 17,5; 18,0; 19,0; 20,0 (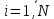 ). ).При уровне значимости α = 0,05 по 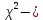 критерию Пирсона критерию Пирсона 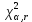 необходимо проверить принадлежность наблюдаемых значений к нормальному распределению. необходимо проверить принадлежность наблюдаемых значений к нормальному распределению.Указания по выполнению задания. Пороговое значение критерия Пирсона 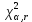 определить с использованием таблицы А.4, а значения вероятностей «попадания» в интервалы – с использованием таблицы А.2 приложения А. определить с использованием таблицы А.4, а значения вероятностей «попадания» в интервалы – с использованием таблицы А.2 приложения А.По результатам выполнения задания сформулировать выводы. Выполнение задания. Задание выполняется в несколько этапов. Вначале выполним разбиение наблюдений на интервалы равной протяженности. Оценка протяженности единичного интервала 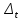 и числа интервалов kвыполняется по формулам и числа интервалов kвыполняется по формулам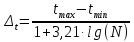 ; (1.1) ; (1.1)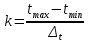 . (1.2) . (1.2)После подстановки исходных данных в (1.1) и (1.2)получим 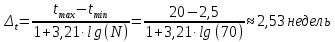 ; ;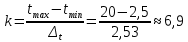 интервалов. интервалов.Исходя из удобства расчетов полученные значения округляем до целочисленного вида и окончательно устанавливаем: 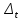 = 3 недели; k = 6. = 3 недели; k = 6. В сгруппированном виде наблюдения представлены в таблице 1.1.
Примечание. В таблице 1.1 круглая скобка означает исключение, а квадратная – включение значений, совпадающих с границей. По исходному ряду tiрассчитаем среднее 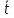 и среднее квадратическое отклонение и среднее квадратическое отклонение 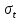 наблюдений наблюдений 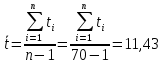 недели; недели;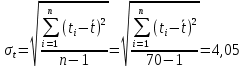 недель. недель.При нормальном распределении вероятность 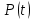 определяется уравнением определяется уравнением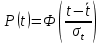 , (1.3) , (1.3) где Ф(z) – функция Лапласа – для задаваемого t определяется по таблице квантилей нормального распределения (таблица А.4). Вход в таблицу осуществляется по предварительно рассчитанному подоператорному значению z, которое, помимо t зависит от двух параметров нормального распределения: 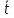 и и 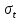 . .С учетом (1.3) рассчитаем теоретические частоты попадания в интервалы: 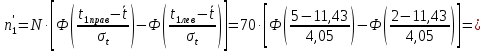 = 70·[Ф(–2,50) – Ф(–1,60)] = 70·(0,055–0,006) = 3,6; 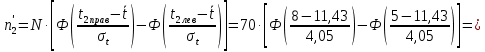 = 70·[Ф(–0,85) – Ф(–1,60)] = 70·(0,198–0,055) = 10,3; 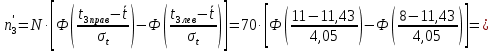 = 70·[Ф(–0,10) – Ф(–0,85)] = 70·(0,460–0,198) = 18,7; 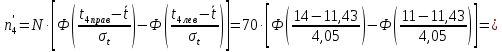 = 70·[Ф(0,65) – Ф(–0,10)] = 70·(0,742–0,460) = 20,1; 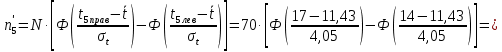 = 70·[Ф(1,40) – Ф(0,65)] = 70·(0,919–0,742) = 12,8; 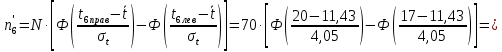 = 70·[Ф(2,10) – Ф(1,40)] = 70·(0,982–0,919) = 4,6. Далее рассчитаем фактическое значение критерия Пирсона 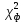 по формуле по формуле . (1.4) . (1.4)Подставив исходные данные в (2.4)получим: 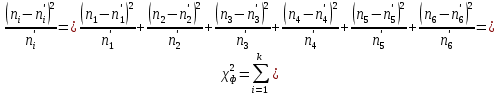 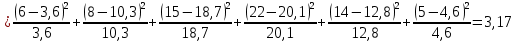 . .Рассчитаем число степеней свободы r = k – s = 6 – 2 = 4, где: k – число интервалов; s – число параметров описывающих рассматриваемое распределение. Нормальное распределение описывают двумя параметрами: средним 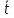 и СКО и СКО 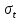 . .Для r = 4 и доверительной вероятности P = 0,95 (уровень значимости α = 0,05) по таблице А.4 определяем пороговое значение критерия Пирсона 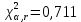 . .Так как 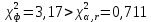 , то предположение о нормальном законе распределения результатов наблюдений не подтверждается. , то предположение о нормальном законе распределения результатов наблюдений не подтверждается.Для наглядности на рисунке 1.1 показаны гистограмма фактических и график нормально распределенных частот попадания наблюдений в интервалы. 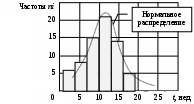 Рисунок 1.1 – Фактическое и нормальное распределения частот Выводы по заданию 1 (например): 1. Исходя из условия задания, была произведена проверка гипотезы о возможности использования нормального распределения для оценки показателей надежности подшипниковых узлов тормозных колес шасси. По стандартным методам были определены значения критериев Пирсона: фактическое 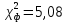 и пороговое и пороговое 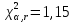 . Так как фактическое значение незначительно превышает пороговое (критическое) значение, то использовать нормальное распределение для оценки надежности подшипниковых узлов нельзя. . Так как фактическое значение незначительно превышает пороговое (критическое) значение, то использовать нормальное распределение для оценки надежности подшипниковых узлов нельзя.2. Достоверность проверки гипотезы о возможности использования нормального распределения для оценки показателей можно повысит за счет: увеличения числа наблюдений(N 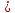 70); 70);повышения уровня значимости(  ); );использования других критериев (Фишера, Колмогорова, Дарбина-Уотсона, Стьюдента); необходимо обеспечить равные условия всем наблюдаемым объектам. 3. Повысить надежность подшипниковых узлов тормозных колес шасси можно за счет реализации следующих организационно-технических мероприятий: проведения тренажей с летным составом по корректному торможению колес на этапе посадки самолета; проведения тренажей с инженерно-техническим составом по контролю смазки подшипников тормозных колес и корректной замене смазки; формирования технической записки о необходимости замены сорта смазки с НК-50 (СТ) на более эффективные сорта. Задание 2 – Оценка параметров теоретических распределений Текст задания и исходные данные. С целью обеспечения возможности последующей параметрической оценки надежности колес шасси воздушного судна необходимо определить значения параметров трех теоретических законов распределения: экспоненциального (параметр 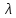 ), нормального (параметры ), нормального (параметры 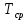 и и 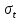 ), Вейбулла (параметры a и b). ), Вейбулла (параметры a и b). Вариационный ряд исходных данных представляет собой следующую последовательность 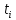 (в неделях): 4,0; 5,0; 7,5; 7,5; 8,0; 9,0; 9,5; 9,5; 9,5; 10,5; 11,0; 11,5; 11,5; 12,5; 12,5; 13,0; 13,0; 13,0; 13,5; 13,5; 13,5; 14,0; 14,0; 14,5; 14,5; 15,0; 15,0; 15,0; 15,5; 15,5; 16,0; 16,0; 16,5; 16,5; 16,5; 17,0; 17,0; 17,0; 17,0; 17,0; 17,5; 17,5; 17,5; 18,0; 18,0; 18,0; 18,0; 18,0; 18,0; 18,0; 18,5; 18,5; 19,0; 19,5; 19,5; 19,5; 19,5; 20,0; 20,0; 20,0; 20,0; 20,5; 20,5; 21,0; 21,0; 22,0; 22,0; 22,5; 23,0; 23,5 ( (в неделях): 4,0; 5,0; 7,5; 7,5; 8,0; 9,0; 9,5; 9,5; 9,5; 10,5; 11,0; 11,5; 11,5; 12,5; 12,5; 13,0; 13,0; 13,0; 13,5; 13,5; 13,5; 14,0; 14,0; 14,5; 14,5; 15,0; 15,0; 15,0; 15,5; 15,5; 16,0; 16,0; 16,5; 16,5; 16,5; 17,0; 17,0; 17,0; 17,0; 17,0; 17,5; 17,5; 17,5; 18,0; 18,0; 18,0; 18,0; 18,0; 18,0; 18,0; 18,5; 18,5; 19,0; 19,5; 19,5; 19,5; 19,5; 20,0; 20,0; 20,0; 20,0; 20,5; 20,5; 21,0; 21,0; 22,0; 22,0; 22,5; 23,0; 23,5 (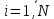 ). ).Считать, что общее число наблюдаемых объектов N = 80. Указания к выполнению задания. Значение вспомогательной переменной dопределить по таблице А.5 приложения А. По результатам выполнения задания сформулировать выводы. Выполнение задания. Задание выполняем в три этапа – по числу заданных теоретических законов распределения наработки на отказ. Оценку параметра 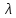 экспоненциального распределения рассчитываем по формуле экспоненциального распределения рассчитываем по формуле 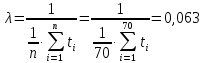 1/нед. 1/нед.Оценку параметра места  и параметра формы и параметра формы  нормального распределения выполняем по формулам нормального распределения выполняем по формулам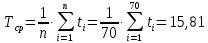 нед.; нед.;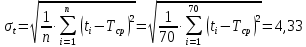 нед. нед.Оценку параметра места  и параметра формы и параметра формы 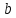 распределения Вейбулла выполняем в следующем порядке. распределения Вейбулла выполняем в следующем порядке.Вначале рассчитаем по формулам значения вспомогательных переменных  и и  . Получим: . Получим: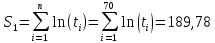 ; ;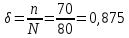 . .Затем по формуле рассчитаем предварительной значение параметра формы 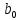 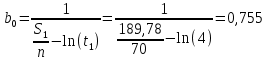 . .По таблице А.5 приложения А определим значение вспомогательной переменной 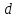 . Имеем . Имеем 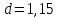 . Далее определяем окончательное значение параметра формы . Далее определяем окончательное значение параметра формы 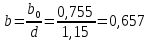 . .Далее по формулам рассчитываем значения вспомогательных переменных 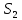 и и 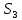 . Имеем: . Имеем: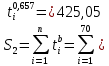 ; ; . .Значение параметра места aрассчитываем по формуле 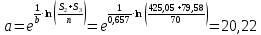 . .Выводы по заданию 2 (например): 1. В соответствии с заданием рассчитаны численные значения параметров теоретических распределений: для экспоненциального распределения параметр 𝜆 = 0,063; для нормального распределения параметр места Tср = 15,81, а параметр формы 𝜎t = 4,33; для распределения Вейбулла параметр места a = 20,22, а параметр формы b = 0,657. 2. Повысить точность определения параметров теоретических распределений можно за счет: повышения объема исходной выборки (n), увеличения численности наблюдаемых объектов (N), использования более корректных методик расчетов. Задание 3 – Параметрическая оценка безотказности воздушного судна Текст задания и исходные данные. Из опыта эксплуатации парка самолетов установлены следующие законы распределения наработки до отказа и значения параметров этих распределений для групп объектов: - шасси – экспоненциальное распределение с параметром 𝜆 = 0,002; - планер – распределение Вейбулла с параметрами: места a = 84,5; формы b = 0,45; - силовая установка – нормальное распределение с параметрами: среднее 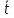 = 602; среднее квадратическое отклонение = 602; среднее квадратическое отклонение 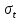 = 364; = 364;- бортовое авиационное и радиоэлектронное оборудование (АиРЭО) – логарифмически нормальное распределение с параметрами: среднее 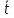 = 4,1; среднее квадратическое отклонение = 4,1; среднее квадратическое отклонение 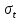 = 3,2. = 3,2.Необходимо выполнить параметрическую оценку вероятности безотказной работы 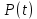 , вероятности отказа , вероятности отказа 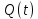 , интенсивности отказов , интенсивности отказов 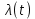 и средней наработки до отказа и средней наработки до отказа 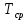 для следующих моментов наработки t, ч: 10; 50; 100; 500; 1000. По полученным точкам построить графики безотказности в диапазоне 10…1000 ч. для следующих моментов наработки t, ч: 10; 50; 100; 500; 1000. По полученным точкам построить графики безотказности в диапазоне 10…1000 ч.Для перечисленных моментов наработки рассчитать результирующую вероятность безотказной работы 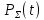 для всего самолета считая, что на функциональной схеме планер, шасси, силовая установка и бортовое АиРЭО соединены последовательно. для всего самолета считая, что на функциональной схеме планер, шасси, силовая установка и бортовое АиРЭО соединены последовательно.По результатам выполнения задания сформулировать выводы. Указания по выполнению задания. По результатам выполнения задания сформулировать выводы. Выполнение задания. Задание выполняется в шесть этапов– по числу групп оцениваемых групп объектов, с учетом результирующей оценки безотказности и необходимости формулировки выводов. Оценка безотказности шасси (этап 1): вероятность безотказной работы для заданных наработок рассчитывается по формуле 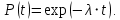 (3.1) (3.1)Подставив исходные данные в (3.1) получим: 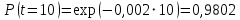 ; ;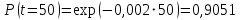 ; ;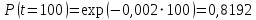 ; ;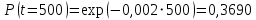 ; ;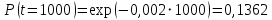 ; ;вероятность отказа для заданных наработок рассчитывается по формуле 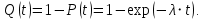 (3.2) (3.2)Подставив исходные данные в (3.2) получим: 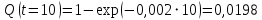 ; ; ; ;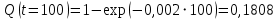 ; ;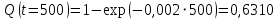 ; ;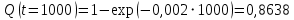 ; ;интенсивность отказов для всех наработок рассчитывается по формуле  , (3.3) , (3.3)Подставив исходные данные в (3.3) получим: 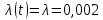 1/ч; 1/ч; средняя наработка до отказа для всех наработок рассчитывается по формуле 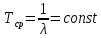 . (43.4) . (43.4)Подставив исходные данные в (3.4) получим: 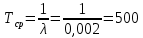 ч. ч.Графики вероятности безотказной работы и вероятности отказа шасси представлены на рисунке 3.1.  Рисунок 3.1 – Вероятности отказа и безотказной работы шасси Оценка безотказности планера (этап 2): вероятность безотказной работы для заданных наработок рассчитывается по формуле 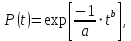 (3.5) (3.5)Подставив исходные данные в (3.5) получим: 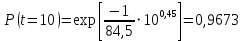 ; ; ; ;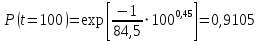 ; ;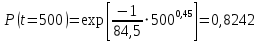 ; ; ; ;вероятность отказа для заданных наработок рассчитывается по формуле 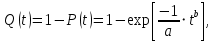 (3.6) (3.6)Подставив исходные данные в 4.6) получим: 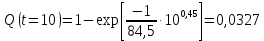 ; ;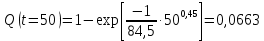 ; ;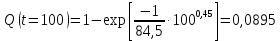 ; ;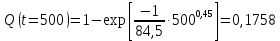 ; ;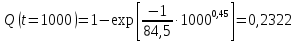 ; ;интенсивность отказов для заданных наработок рассчитывается по формуле  (3.7) (3.7)Подставив исходные данные в (3.7) получим:  1/ч; 1/ч; 1/ч; 1/ч;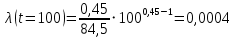 1/ч; 1/ч;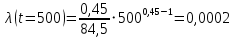 1/ч; 1/ч;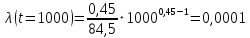 1/ч; 1/ч;средняя наработка до отказа рассчитывается по ниже представленной формуле, а значение гамма–функции определяется по таблице А.1. 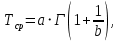 (3.8) (3.8)Подставив исходные данные в (3.8) получим: 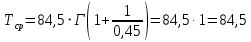 ч. ч.Графики вероятности безотказной работы, вероятности отказа и интенсивности отказов планера представлены на рисунке 3.2. 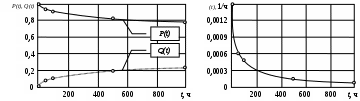 Рисунок 3.2 – Вероятность отказа, вероятность безотказной работы и интенсивность отказов планера Оценка безотказности силовой установки (этап 3): вероятность безотказной работы для заданных наработок рассчитывается по ниже представленной формуле с использованием таблицы А.2 и примечаний к ней 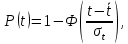 (3.9) (3.9)Подставив исходные данные в (3.9) получим: 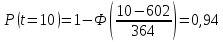 ; ;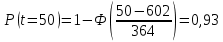 ; ;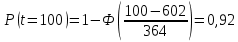 ; ;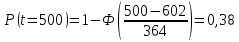 ; ;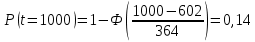 ; ;вероятность отказа для заданных наработок рассчитывается по формуле 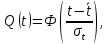 (3.10) (3.10)Подставив исходные данные в (3.10) получим: 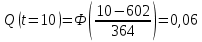 ; ;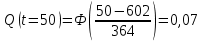 ; ; ; ;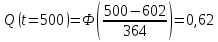 ; ; ; ;интенсивность отказов для заданных наработок рассчитывается по ниже представленной формуле с использованием таблицы А.3 и примечаний к ней 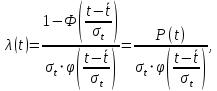 (3.11) (3.11)Подставив исходные данные в (3.11) получим: 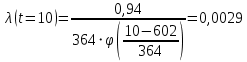 1/ч; 1/ч;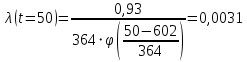 1/ч; 1/ч; 1/ч; 1/ч;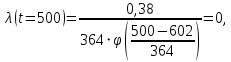 0045 1/ч; 0045 1/ч;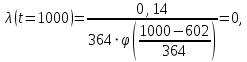 011 1/ч; 011 1/ч;средняя наработка до отказа для всех наработок рассчитывается по формуле Тср =  . (3.12) . (3.12)Подставив исходные данные в (3.12) получим: Тср =  ч. ч.Графики вероятности безотказной работы, вероятности отказа и интенсивности отказов силовой установки представлены на рисунке 3.3. 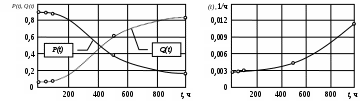 Рисунок 3.3 – Вероятность отказа, вероятность безотказной работы и интенсивность отказов силовой установки Оценка безотказности бортового АиРЭО (этап 4): вероятность безотказной работы для заданных наработок рассчитывается по формуле  (3.13) (3.13)Подставив исходные данные в (4.13) получим: 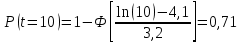 ; ;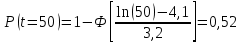 ; ;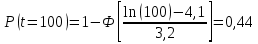 ; ;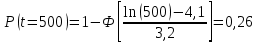 ; ;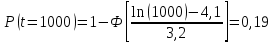 ; ;вероятность отказа для заданных наработок рассчитывается по формуле 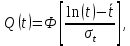 (3.14) (3.14)Подставив исходные данные в (3.14) получим: 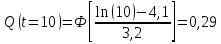 ; ;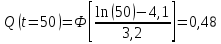 ; ;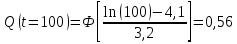 ; ;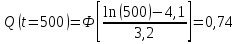 ; ;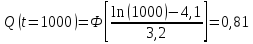 ; ;интенсивность отказов для заданных наработок рассчитывается по ниже представленной формуле с использованием таблицы А.3 и примечаний к ней 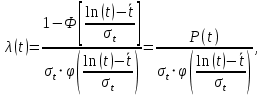 (3.15) (3.15)Подставив исходные данные в (3.15) получим: 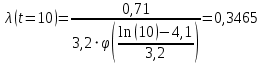 1/ч; 1/ч;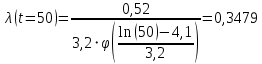 1/ч; 1/ч;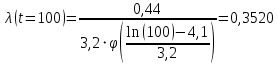 1/ч; 1/ч;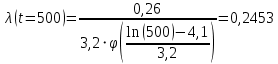 1/ч; 1/ч; 1/ч; 1/ч;средняя наработка до отказа для всех наработок рассчитывается по формуле 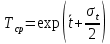 . (3.16) . (3.16)Подставив исходные данные в (3.16) получим: 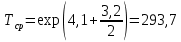 ч. ч.Графики вероятности безотказной работы, вероятности отказа и интенсивности отказов бортового АиРЭО представлены на рисунке 3.4. 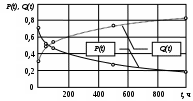  Рисунок 3.4 – Вероятность отказа, вероятность безотказной работы и интенсивность отказов бортового АиРЭО Оценка результирующей вероятности безотказной работы ВС (этап 5). В соответствии с заданием функциональная схема всего воздушного судна имеет вид, представленный на рисунке 3.5.  Рисунок 3.5 – Функциональная схема воздушного судна Расчет результирующей вероятности безотказной работы всего ВС  выполняется по формуле выполняется по формуле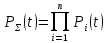 . (3.17) . (3.17)Подставив ранее полученные данные в (3.17) получим: 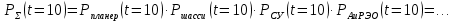 ; ;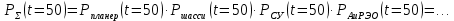 ; ;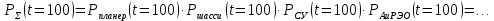 ; ;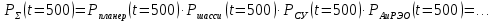 ; ;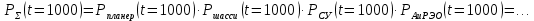 ; ;График вероятности безотказной работы ВС 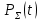 представлен на рисунке 3.6. представлен на рисунке 3.6.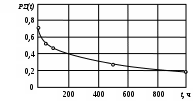 Рисунок 3.6 – Результирующая вероятность безотказной работы всего ВС Выводы по заданию 3 (например): 1. В соответствии с заданием выполнена оценка безотказности самолета. В частности вероятности безотказной работы P(t), вероятности отказа Q(t), интенсивности отказов λ(t) и средней наработки до отказа Tср для моментов наработки t, ч: 10; 50; 100; 500; 1000. Полученные результаты представлены на рисунке 3.6. 2. Повысить точность расчетов показателей безотказности за счет более точной подборки теоретических распределений для компонент самолета, а также – за счет более точной оценки численных значений параметров подобранных теоретических распределений. 3. Улучшение безотказности компонент самолета возможно за счет выполнения комплекса доработок, повышения квалификационного уровня обслуживающего авиаперсонала, формирования и использования более эффективных режимов, программ и стратегий ТОиР воздушного судна; |

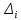 (недели)
(недели)