КР по матлогике и теории алгоритмов. КР по Матлогике и теории алгоритмов Чора А.Н (1). Подпись И. О. Фамилия 20 г
 Скачать 79.23 Kb. Скачать 79.23 Kb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР) Кафедра автоматизированных систем управления (АСУ) ТУСУР (Контрольная работа по дисциплине «Математическая логика и теория алгоритмов») Вариант 4
Томск 2022 №1. Следующее утверждение для произвольных множеств докажите или опровергните (A ∪ B) ∩ C = A ∪ (B ∩ C). (A ∪ B) ∩ C = A ∪ (B ∩ C) Левая часть: (A ∪ B) ∩ C = С ∩ ( A ∪ B) = (С ∩ А) ∪ (С ∩ В) = (А ∩ С) ∪ (В ∩ С) Правая часть: A ∪ (B ∩ C) = (А ∪ В) ∩ (A ∪ C) Вывод: (А ∩ С) ∪ (В ∩ С) ≠ (А ∪ В) ∩ (A ∪ C) – опровергнуто! №2. Является ли формула ((p ⊃ q) & (q ⊃ p) & (p ∨ r) & ¬r) ⊃ p тавтологией? ((p ⊃ q) & (q ⊃ p) & (p ∨ r) & ¬r) ⊃ p = (¬p + q) (¬q + p)(p¬r + r ¬r) → p = = (¬p¬q + ¬pp + q¬q + qp)(p¬r + r¬r) →p = (¬p¬q + 0 + 0 +qp)( p¬r + 0) → p = = (¬p¬q + qp) p¬r →p = (¬pp¬qr + qpp¬r) → =(0 + qpp¬r) → p = ¬q¬p¬¬r + p = = ¬q + ¬p + ¬¬r + p = ¬q + (¬p + p) + r = ¬q + 1 + r = 1 ⇒ Формула является тавтологией №3. Переведите с естественного языка на язык логики предикатов: Кошки бывают только белые и серые. Введем предикаты: С(х) ≡ «кошка» М (х) ≡ « серая кошка» N (x) ≡ «белая кошка» ∃х, ∀х ((С (х) → (М (х) ⊕ N (х)) №4. Переведите с естественного языка на язык логики предикатов: Так как 60 делится на 2 и на 3, то 60 делится на некоторые числа, отличные от 60. Введем предикаты: А ≡ « 60 ∶ 2 » В ≡ « 60 ∶ 3» Р(x) ≡ « 60 ∶ х» S(x) ≡ «х ≠ 60» (А ∪ В) → (Р (х) ⋂ S (х)) №5. Для бинарного отношения x ρ y ⇔ «x + y делится нацело на 3», определенного на множестве Z целых чисел, выясните, какими свойствами оно обладает (рефлексивность, симметричность, антисимметричность, транзитивность) и какими не обладает. Отношение р на множестве х рефлексивно, если ∀х ∈ Х выполняется xRx «хRх» : 3 выполняется не для ∀х ∈ Z (например 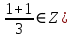 ⇒ нерефлексивно ⇒ нерефлексивноОтношение р на множестве х симметрично, если ∀х, у ∈ Х Хру=урх Отношение р симметрично, т.к. если «х+у» : 3, то и «у+х» : 3 Отношение р транзитивно на множестве х, если ∀х,у,z ∈ Х (Хру) ∧ (ypz) → xpz «х+у : 3» и «х+z : 3», но «х+z : 3» выполняется не для ∀х,у,z ∈ Z 2+4=6:3 4+5=9:3 2+5=7 не делится на 3 - нетранзитивно Отношение р на множестве х антисиммитрично, если ∀х,у ∈ х хRу уRх ⇒ ⇒ х=у «х+у : 3» и «у+х» : 3 выполняется не для ∀х,у ∈ Z 2+4=6:3 4+2=6:3 2≠4 – неантисимметрично Ответ: нерефлексивно, симметрично, нетранзитивно, неантисимметрично № 6. Докажите, что отношение <а, b> p <а, b> p Рефлексивность R (<а, b>, <а, b>) ⇒ a2 + b2 = a2 + b2 ∈ R Симметричность R (<а, b>, a2 + d2 = c2 + b2 ⇒ c2 + b2 = d2+ a2 Транзитивность R (<а, b>, a2 + d2 = c2 + b2 ∪ c2 + m2 = l2 + d2 ⇒ a2 + m2= l2+ b2 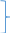 а) a2 + d2 = c2 + b2 ⇔ a2 - b2= c2 - d2 б) c2 + m2 = l2 + d2 ⇔ c2 - d2= l2 - m2 1⋂2 ⇒3 в) a2 + m2 = l2 + b2 ⇔ a2 - b2= l2 - m2 ⇒отношение эквивалентности Классы эквивалентности: точки (a,b) и (c,d) принадлежит одному и тому же классу тогда и только тогда, когда a2 + b2 = c2 + d2 Обозначим любую сторону как радиус ⇒ уравнение окружности 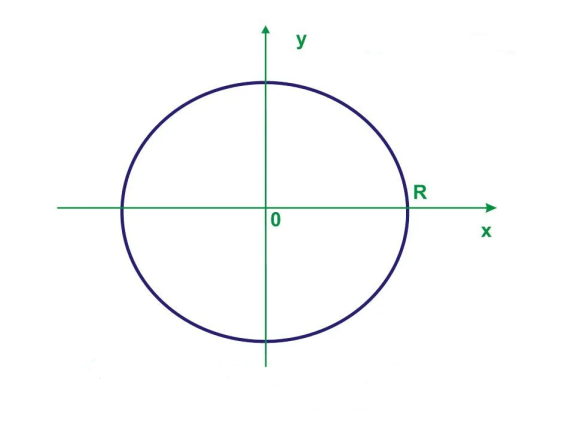 №7. Используя математическую индукцию, докажите равенство 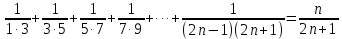 для целого n > 0. для целого n > 0.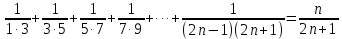 n > 0, n ∈ Z n > 0, n ∈ Zn=1 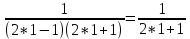 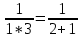 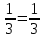 - верно - верно n=k 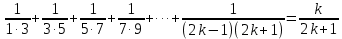 n=k+1 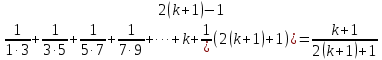  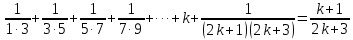 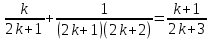 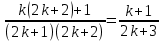 2k2+2k+1 = k+1 4k2+6k+3 2k+3 (2k2+2k+1)(2k+3)=(k+1)(4k2+6k+3) 4k3+6k2+4k2+6k+2k+3=4k3+6k2+2k+4k2+6k+3 4k3+10k2+8k+3=4k3+10k2+8k+3 - верно №8. Расположите следующие 5 функций в порядке увеличения скорости роста (каждая функция есть O (следующая)): 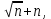 nen , n2(ln n)1000 , n3 – 100n2 , ln n. nen , n2(ln n)1000 , n3 – 100n2 , ln n. 1000 Ответ: ln n , 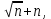 n2(ln n)1000, n3 – 100n2, nen n2(ln n)1000, n3 – 100n2, nen 1000 |
