математика. МАТЕМАТИКА. Подставим в выражение, стоящее под знаком предела, число. Получаем неопределенность вида. Проведем почленное деление на
 Скачать 66.75 Kb. Скачать 66.75 Kb.
|
|
Автономная некоммерческая организация высшего образования «МОСКОВСКИЙ МЕЖДУНАРОДНЫЙ УНИВЕРСИТЕТ» Кафедра экономики Форма обучения: заочная
МОСКВА 2019 1. Вычислить пределы последовательностей а) 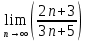 Подставим в выражение, стоящее под знаком предела, «число» 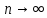 . Получаем неопределенность вида . Получаем неопределенность вида 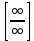 . Проведем почленное деление на . Проведем почленное деление на 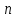 . .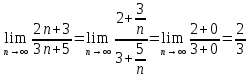 б) 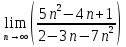 При подстановке  . Получаем неопределенность вида . Получаем неопределенность вида 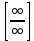 . Проведем почленное деление на старшую степень . Проведем почленное деление на старшую степень 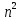 . .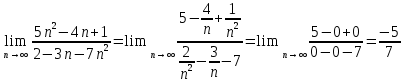 в) 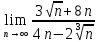 Имеем неопределенность вида 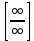 . В каждом из многочленов вынесем старшую степень . В каждом из многочленов вынесем старшую степень 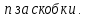 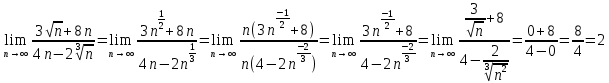 г) 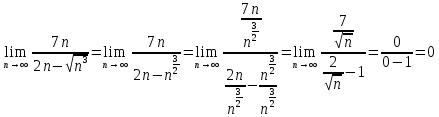 д) 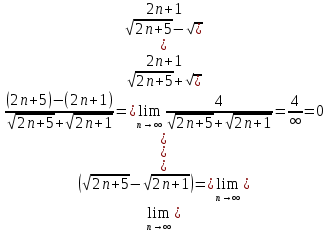 е) 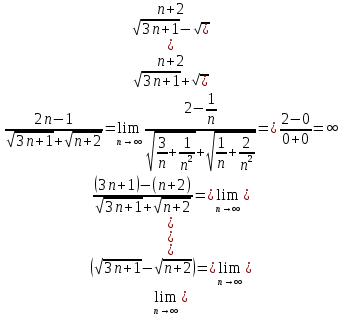 ж) 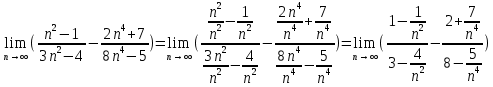 При подстановке  получим: получим: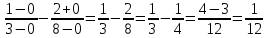 з) 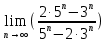 Умножим числитель и знаменатель дроби на 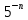 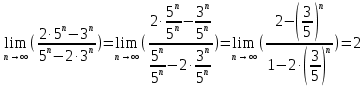 2. Найти производные сложных функций 1) y 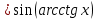 y 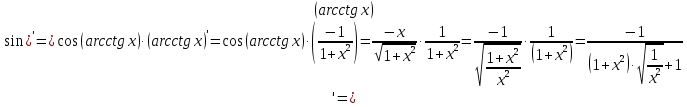 2) y 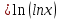 y 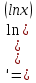 3) y 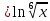 y 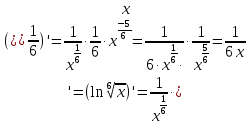 4) y 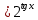 y 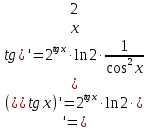 5) y 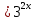 y 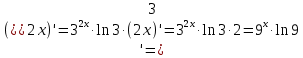 6) y 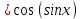 y 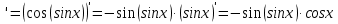 7) y 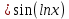 y 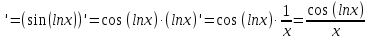 8) y 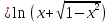 y 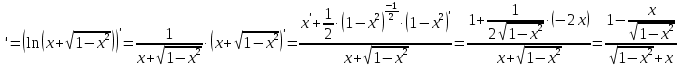 9) y 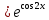 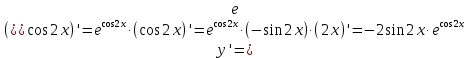 10) y 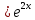 y 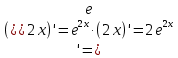 11) y 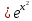 y 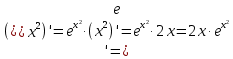 12) y 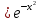 y 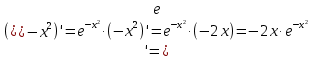 3. Вычислить неопределенный интеграл 1) 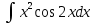 Используем формулу интегрирования по частям 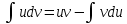 Пусть 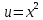 , , 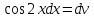 Тогда 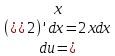 , , 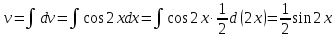 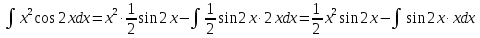 Для интеграла 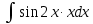 используем еще раз формулу интегрирования по частям используем еще раз формулу интегрирования по частямПусть 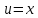 , , 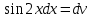 Тогда 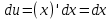 , , 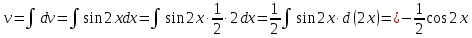 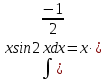 cos2x) cos2x) 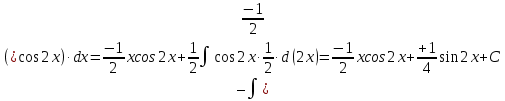 Искомый интеграл равен: 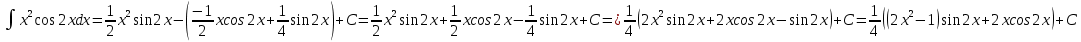 2) 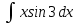 Используем формулу интегрирования по частям 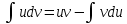 Пусть 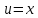 , , 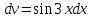 Тогда 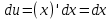 , , 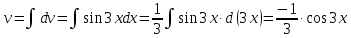 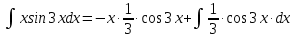 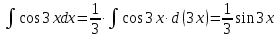 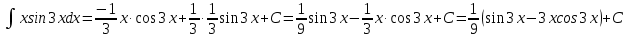 3) 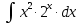 Используем формулу интегрирования по частям 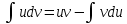 Пусть 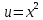 , , 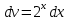 Тогда 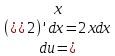 , , 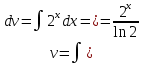 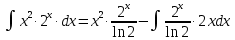 Находи интеграл  Для интеграла 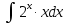 используем еще раз формулу интегрирования по частям используем еще раз формулу интегрирования по частямПусть 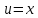 , , 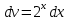 Тогда 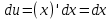 , , 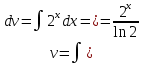 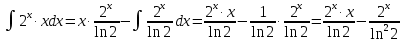 Искомый интеграл равен: 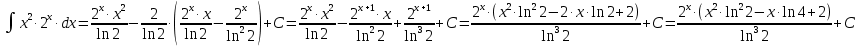 4)  Используем формулу интегрирования по частям 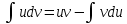 Пусть 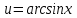 , , 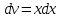 Тогда 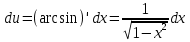 , , 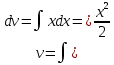 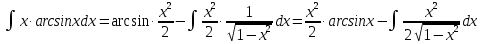 Применим тригонометрические подстановки 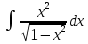 Пусть 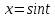 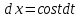 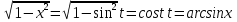 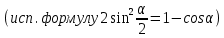 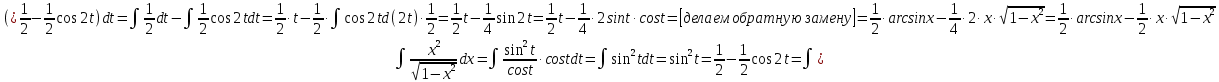 Искомый интеграл: 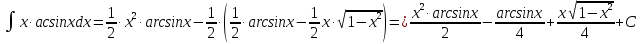 5) 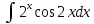 Используем формулу интегрирования по частям 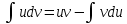 Пусть 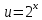 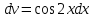 Тогда 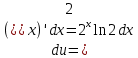 , , 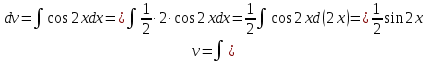 Таким образом, 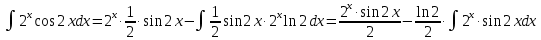  Для последнего интеграла еще раз применим интегрирование по частям: Для последнего интеграла еще раз применим интегрирование по частям: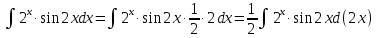 Примем 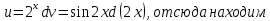 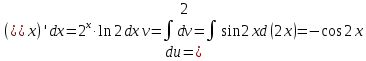 Получаем 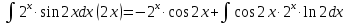 Искомый интеграл равен: 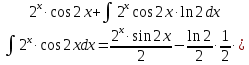 В левой и правой частях уравнения присутствует 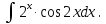 Выразим его из полученного выражения: Выразим его из полученного выражения: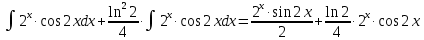 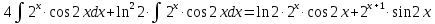 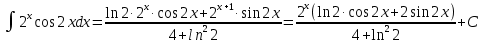 6) 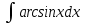 Используем формулу интегрирования по частям 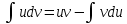 Пусть 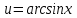 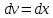 Тогда 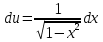 , , 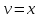 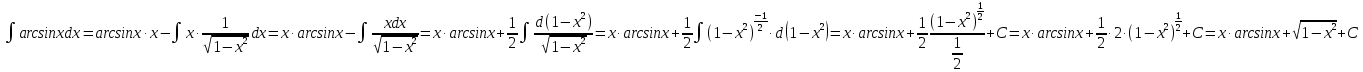 7) 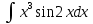 Используем формулу интегрирования по частям 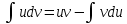 Пусть 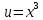 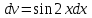 Тогда 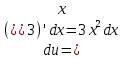 , , 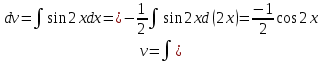 Таким образом, 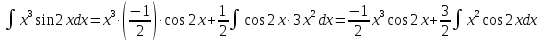 Еще раз применим формулу интегрирования по частям для интеграла: 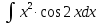 Пусть 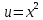 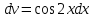 Тогда 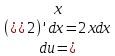 , , 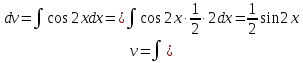 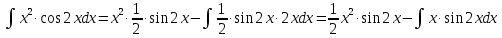 Находим 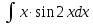 Принимаем 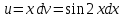 Отсюда 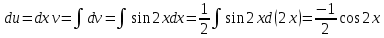 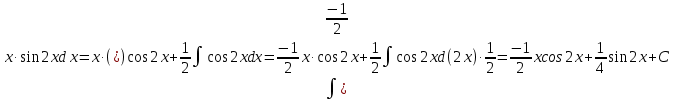 Находим искомый интеграл: 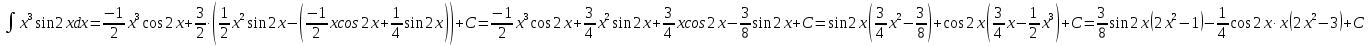 8) 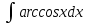 Используем формулу интегрирования по частям 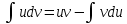 Пусть 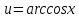 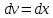 Тогда 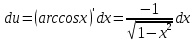 , , 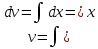 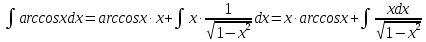 Сделаем замену переменных 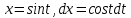 Тогда 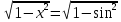 t= t=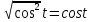 Таким образом 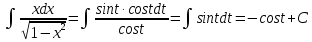 Сделаем обратную замену: 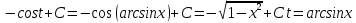 Находим искомый интеграл: 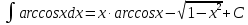 9) 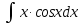 Используем формулу интегрирования по частям 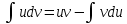 Пусть 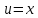 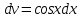 Тогда 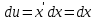 , , 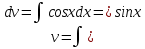 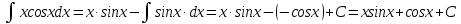 4. Найти частные производные первого и второго порядка 1) 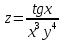 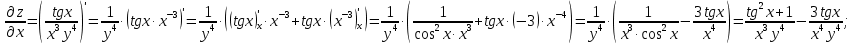 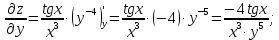 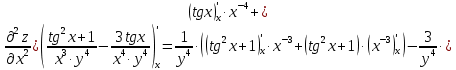 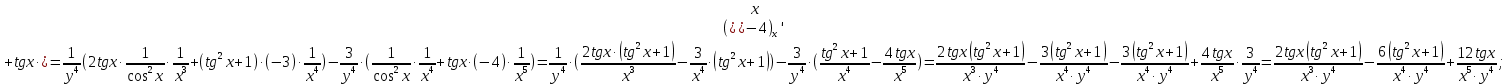 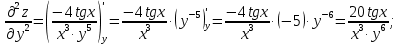 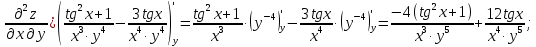 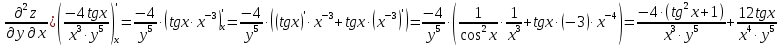 2) 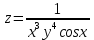 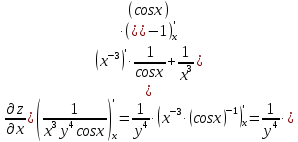 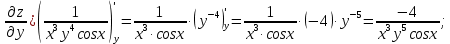 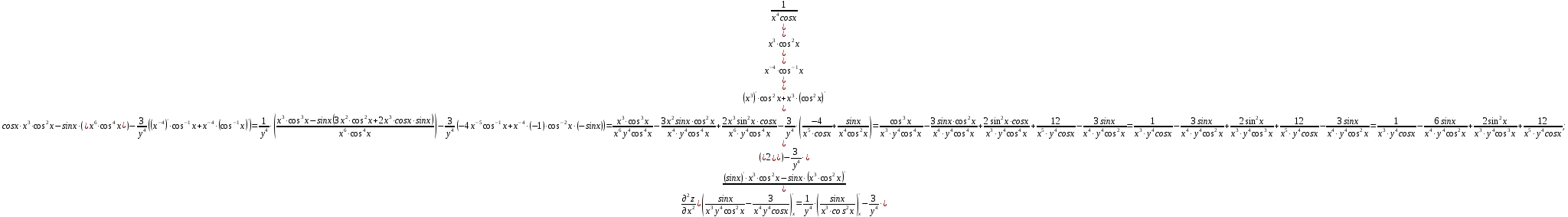 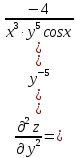 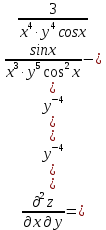 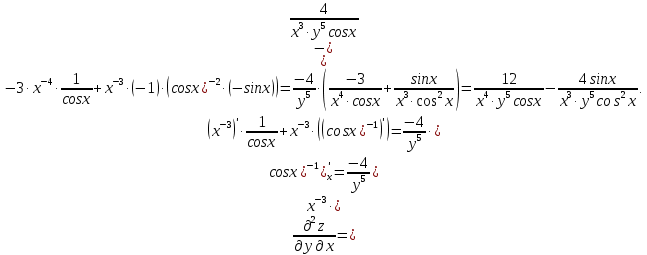 3) 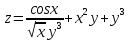 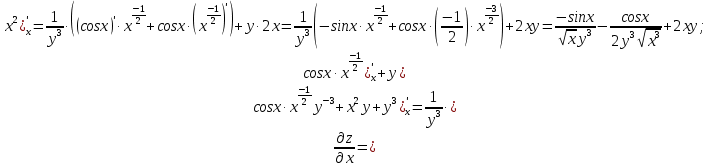 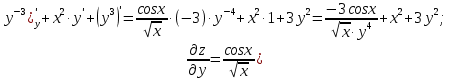 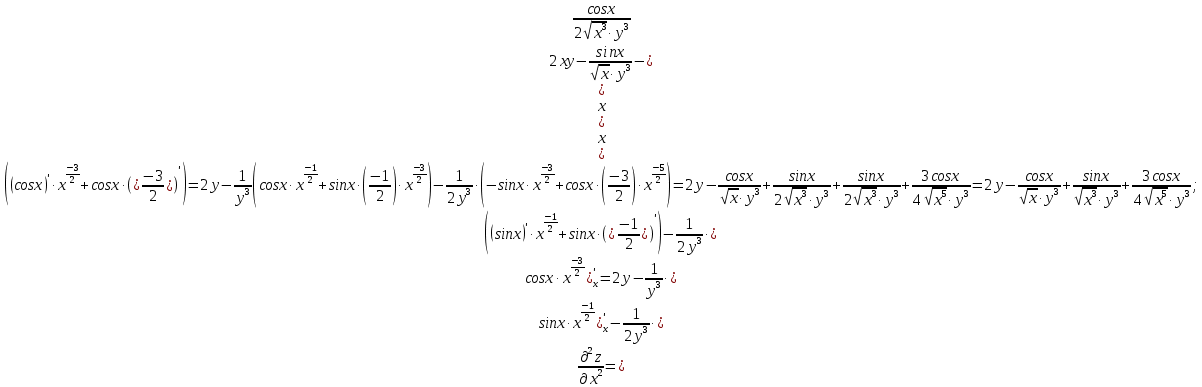 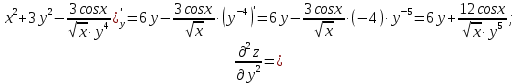 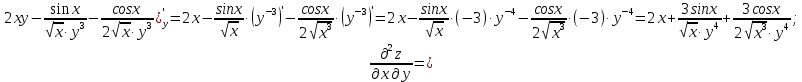 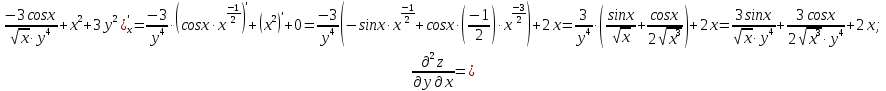 4) 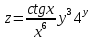 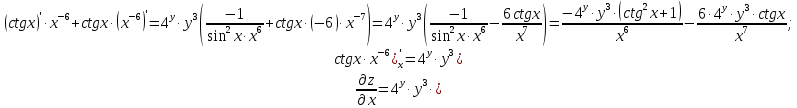 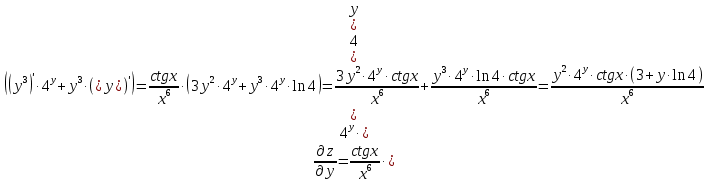 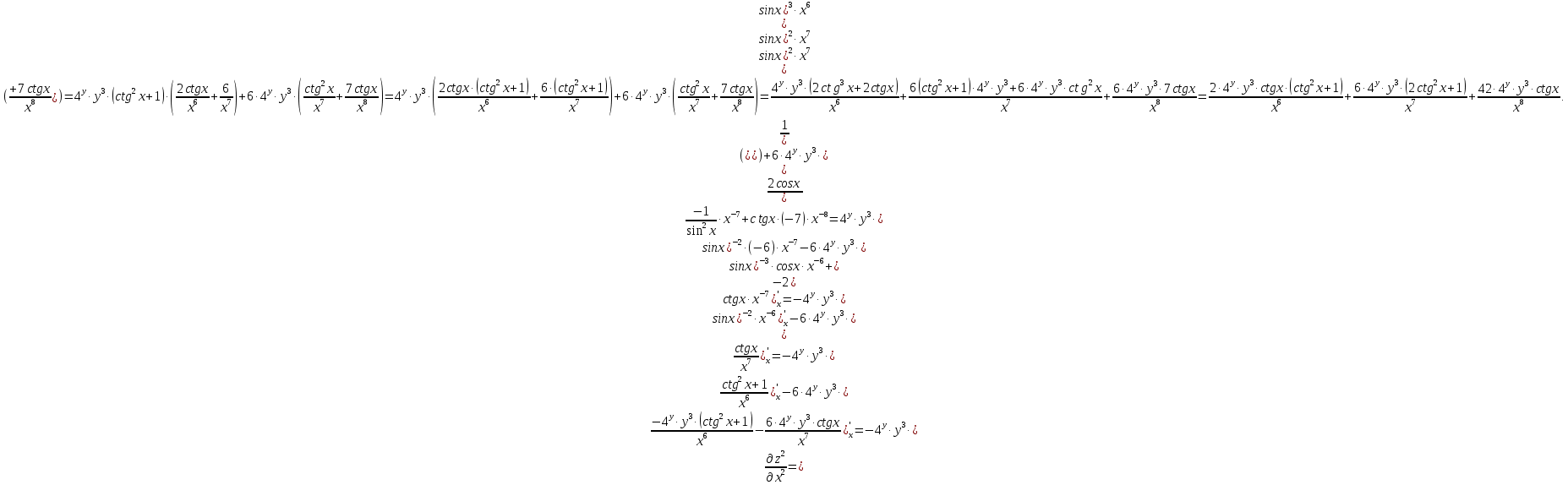 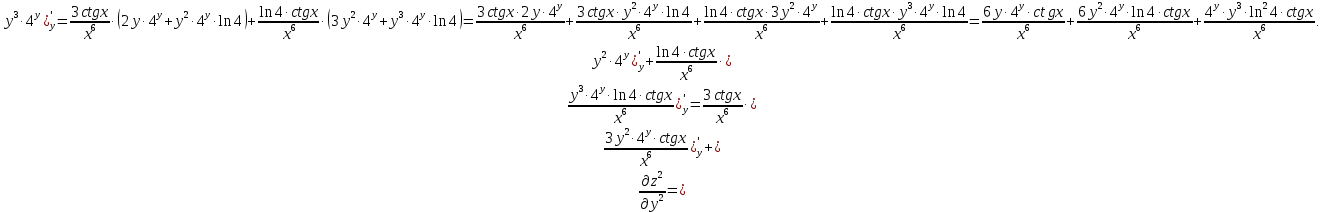 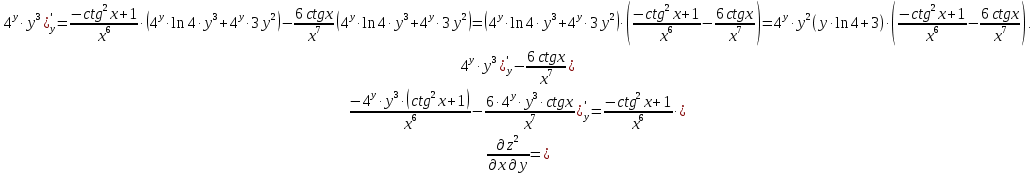 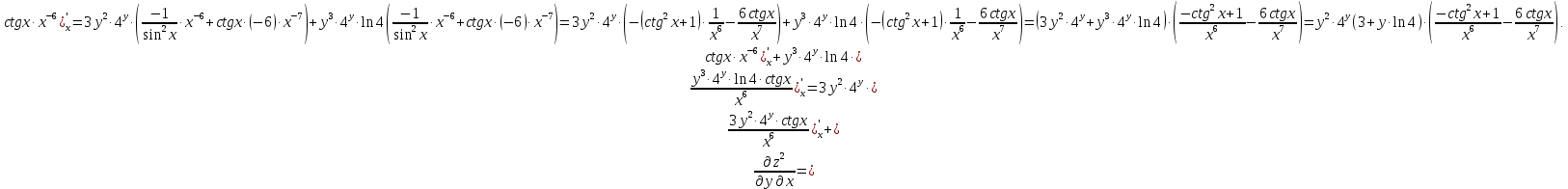 5) 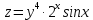 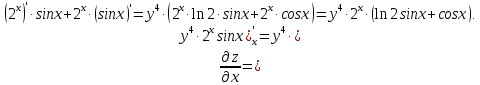 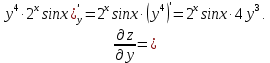 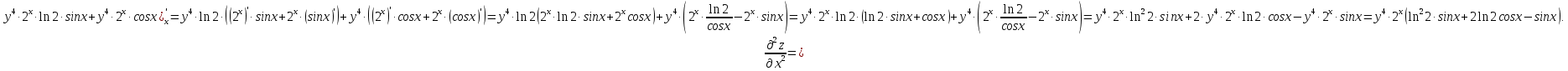 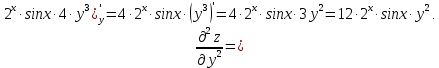 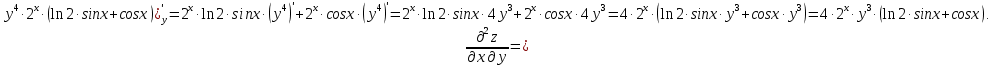 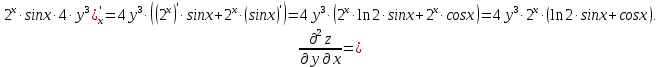 6) 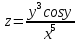 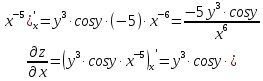 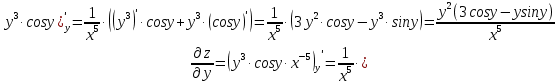 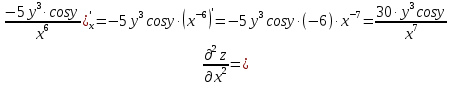 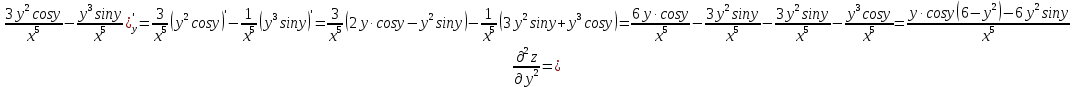 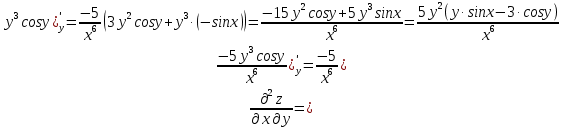 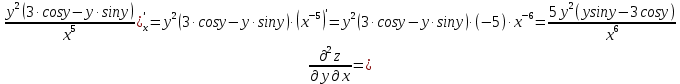 7) 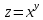 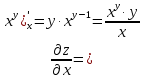 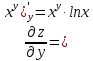 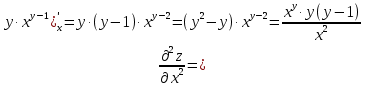 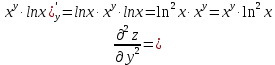 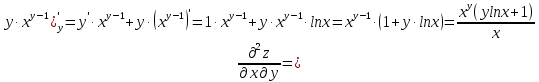 8) 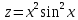   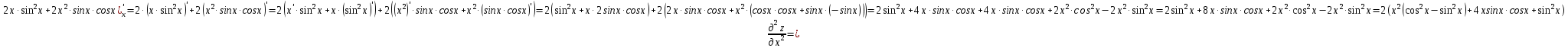 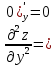 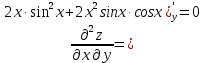 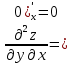 9) 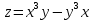 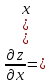 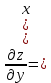 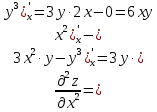 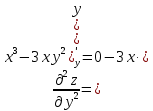 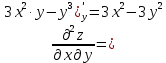 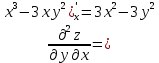 10) 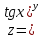 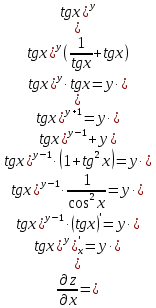 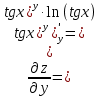 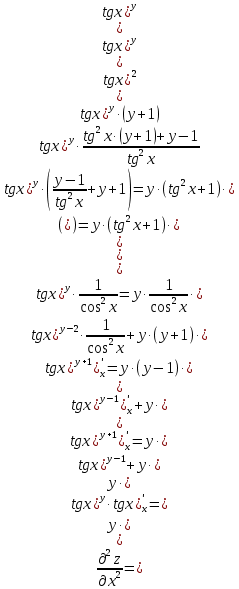 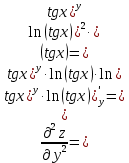 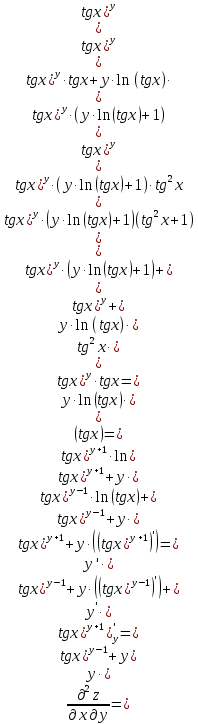 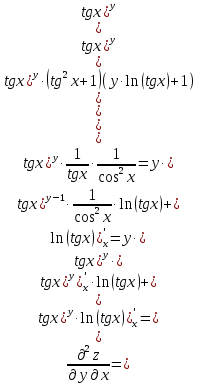 | |||||||||
