Реферат по математической обработке результатов. Погорелова Валерия Аналитическая химия
 Скачать 15.16 Kb. Скачать 15.16 Kb.
|
|
Погорелова Валерия Аналитическая химия. Случайная величина – переменная, принимающая различные значения в зависимости от случая. Погрешность измерения – любое отличие результата измерений от истинного значения измеряемой величины. Точность (достоверность) измерения характеризует малость погрешности, то есть близость измеренной величины к истинной. Погрешности классифицируют по характеру причин, их вызывающих и по способу вычисления. По характеру причин их делят на систематические и случайные, выделяют также промахи. К систематическим относят погрешности, которые вызваны постоянно действующей причиной, постоянны во всех измерениях или меняются по постоянно действующему закону. Они могут быть выявлены и устранены. Правильность (систематическая погрешность) – метрологическая категория, характеризующая малость систематической составляющей погрешности. Случайные погрешности это погрешности, причины появления которых неизвестны. Они могут быть оценены методами математической статистики. Воспроизводимость (случайная погрешность или разброс относительно среднего из результатов измерений) характеризует малость случайной составляющей погрешности. Промах – это погрешность, резко искажающая результат анализа и обычно легко обнаруживаемая, вызванная, как правило, небрежностью или некомпетентностью аналитика. Все возможные значения случайной величины образуют генеральную совокупность. Конечное число n значений из генеральной совокупности – выборочная совокупность (выборка), n – объем выборки. По способу вычисления погрешности можно подразделить на абсолютные и относительные. Абсолютная погрешность равна разности среднего значения  величины x и истинного значения величины x и истинного значения 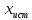 этой величины: этой величины: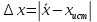 Относительная погрешность может быть выражена в долях или процентах: 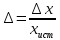 или или 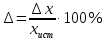 Доверительный интервал – интервал, которому принадлежат значения случайной величины с доверительной вероятностью. Основные параметры выборки Среднее значение выборки – это среднее арифметическое значений, составляющих выборку: 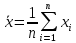 Выборочная дисперсия характеризует среднее рассеяние значений выборки относительно ее среднего значения: 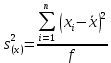 , где , где 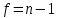 – число степеней свободы. – число степеней свободы.Выборочное стандартное отклонение – это квадратный корень из дисперсии выборки: 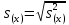 Выборочное стандартное отклонение имеет ту же размерность, что и сама случайная величина x, в отличие от дисперсии, имеющей размерность, равную квадрату размерности случайной величины x. Относительное стандартное отклонение – отношение выборочного стандартного отклонения к выборочному среднему:  Стандартное отклонение среднего определяется по формуле: 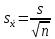 Следовательно, дисперсия среднего результата в n раз меньше дисперсии единичного результата химического анализа. Таблица 1. Значения критерия QP,f
Таблица 2. Значения коэффициентов Стьюдента tP,f
Выборочный анализ титриметрических данных Таблица 3. Результаты стандартизации раствора соляной кислоты
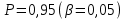 Вариационный ряд (1): 8,75; 8,80; 8,80; 8,80; 8,80; 8,80; 8,82; 8,82. 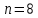 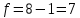 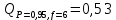 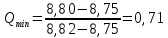 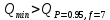 , следовательно, , следовательно, 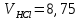 является грубым промахом на уровне значимости является грубым промахом на уровне значимости 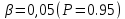 и исключается из выборки. и исключается из выборки.Вариационный ряд (2): 8,80; 8,80; 8,80; 8,80; 8,80; 8,82; 8,82. 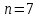  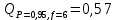 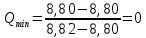 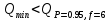 , следовательно, , следовательно, 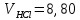 не является грубым промахом на уровне значимости не является грубым промахом на уровне значимости 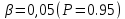 . .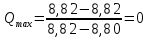 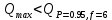 , следовательно, , следовательно, 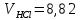 не является грубым промахом на уровне значимости не является грубым промахом на уровне значимости 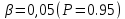 . .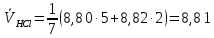 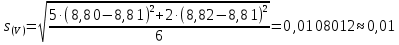 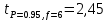 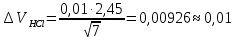 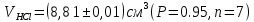 Список используемой литературы Основы аналитической химии. В 2 т. Т. 1 : учебник для студ. учреждений высш. образования / [Т.А. Большова и др.] ; под ред. Ю.А. Золотова. – 6-е изд., перераб. и доп. – М. : Издательский центр «Академия», 2014. – 400 с. Бобрешова О.В., Паршина А.В. Основы химической метрологии и хемометрики Часть 1 / О.В. Бобрешова, А.В. Паршина. – Воронеж : Издательский дом ВГУ, 2007. – 17 с. Чарыков А.К. Математическая обработка результатов химического анализа : Учеб. пособие для вузов. – Л.: Химия, 1984. – 168 с., ил. Кристиан Г. Аналитическая химия. В 2 т. Т. 1 / Г. Кристиан ; пер. с англ. – М. : БИНОМ. Лаборатория знаний, 2009. – 623 с. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
