сила денег. Покупательная способность денег
 Скачать 1.71 Mb. Скачать 1.71 Mb.
|
|
§ 4. Новые исчисления MV и V для 1896-1909 гг. MV. Наша следующая задача - отыскать скорость обращения денег. Вычисление скорости обращения денег представляет большие затруднения, которые фактически рассматривались обычно как непреодолимые. Это мнение было удачно выражено Jevons'ом [Money and the Mechanism of Exchange (London). P. 336.], который писал: “Я никогда не встречал ни одной попытки определить в какой-либо стране среднюю скорость денежного обращения, и я не был в состоянии мыслить какие-либо средства приблизиться к изучению этого вопроса иначе как в обратном порядке. Если мы знаем сумму произведенных обменов и количество использованных денежных знаков, то посредством деления можем получить среднюю цифру, сколько раз денежные знаки сделали оборот, но данных для этого, как я только что указал, совершенно недостаточно”. Однако, как мы увидим дальше, в настоящее время существуют данные, могущие раскрыть “сумму действительных меновых сделок”, или MV. В самом деле эта цифра равна общей сумме денег, вложенных в банки, плюс общая сумма выплаченной денежной заработной платы плюс еще небольшое количество разнообразных платежей. Имея MV и М без сомнения, легко путем деления получить V. Формула для получения MV настолько же проста, насколько вначале она может казаться таинственной. Главная особенность метода, которым представлена эта формула, и главная характерная черта, которая делает его практически применимым, состоят в том, что этот метод пользуется банковскими отчетами и другими доступными проверке статистическими данными как средствами определения общей суммы денежных сделок. Метод этот основан на идее, что деньги, находящиеся в обращении, и деньги, лежащие в банках, не являются двумя независимыми сосудами, но непрерывно текут из одного в другой и что приливы и отливы денег в банках, отмечаемые в отчетах, могут быть использованы для выяснения их обращения вовне. Величина обращения денег была бы ясна из банковских отчетов, если бы было справедливо, что каждый вышедший из банков доллар будет обращаться один, и только один, раз, пока он снова не будет вложен в банк. При этих обстоятельствах годовой поток денежного обращения был бы в точности равен годовому отливу из банков перед обращением, точно так же как и годовой сумме вкладов в банки после обращения. Так как мы имеем отчеты относительно первого и последнего количества, т.е. о востребованиях и вложениях денег, то мы тем самым располагаем средством для определения и промежуточной стадии, т.е. обмена денег на товары. Обычное денежное обращение, за исключением случаев, когда деньги переходят из рук в руки чаще одного раза между временем истребования их из банка и обратного вложения в него, равно потоку денег, проходящему через банки. Но действительность, однако, не так проста, потому что изъятые из банков деньги часто обращаются больше одного раза. Но даже вплетающиеся осложнения следуют определенным законам. Они не уничтожают значения банковских отчетов, но только делают их несколько более трудными для понимания. Мы попробуем указать здесь, во-первых, что в действительности большая часть денег обращается вне банка только один раз, как в только что указанном гипотетическом случае, во-вторых, что если эти деньги идут на заработную плату, то они обычно обращаются дважды и, в-третьих, что деньги только в редких случаях обращаются три или более раза, прежде чем они совершат свой путь обратно в банк. Это положение обозначает, что, подобно чекам, деньги обычно вне банка обращаются только один раз, но когда они проходят через руки невкладчиков, т.е. практически через руки людей, живущих на заработную плату, то они обращаются еще раз, прибавляя, таким образом, сумму заработной платы к сумме обычного обращения денег, которая, как мы уже видели, равна потоку денег, проходящих через банки. Мы рисуем себе совершенно ложную картину денежного обращения в современном обществе, когда воображаем, что оно представляет собой непрерывную цепь передач от одного лица к другому. Если бы существовала такая цепь, то, как говорит Jevons, она находилась бы вне достижений статистики. Но мы можем нарисовать более правдивую картину, принимая банк за “дом” для денег, а обращение денег - за временное отсутствие их из этого “дома”. Если такое описание справедливо, то обращение денег очень немногим отличается от обращения чеков. Как те, так и другие выполняют одну или, во всяком случае, немного сделок вне банка, а затем возвращаются “домой”, чтобы дать отчет о сделанном ими пути. Общая сумма денег, вложенных в банки, как это указано в приложении, в 1896 г. равнялась приблизительно 10 млрд. долл., а общая сумма расходов невкладчиков - около 6 млрд. долл., из которых 4 1/2 млрд. состояли из расходов лиц, живущих на заработную плату, остальное же количество в формуле денежного обращения составляет меньше 1 млрд.; общая сумма денежного обращения составляет, таким образом, около 16 млрд. Для 1909 г. соответствующие цифры следующие: вложенные деньги - 21 млрд., расходы невкладчиков - 13 млрд., остальное количество - около 1 млрд., что составляет в общем 35 млрд. долл. Следующая таблица резюмирует эти выводы (в млрд. долл.)
V. Для того чтобы получить скорость обращения денег, общая сумма обращения MV (16 млрд. для 1896 г. или, точнее, 16,2 млрд.) должна быть разделена на количество денег М, бывших в обращении в 1896 г. Это количество исчисляется в 870 млн. долл. Отсюда скорость обращения равна 16 200 млн.: 870 млн. = 18,6, т. е. около 19 раз в год. Другими словами, деньги оставались на руках в среднем около 365:19, что дает от 19 до 20 дней. Если я вполне учел ошибку, какая могла быть сделана в этом вычислении, то она не превышает двух-трех дней. Для 1909 г. скорость обращения денег исчисляется делением общей суммы обращения (35,1 млрд.) на количество денег в обращении (1,63 млрд.), что дает 21,5, т. е. около 22 раз в год, т. е. один раз в 17 дней. Из этого мы заключаем, что скорость обращения денег в 1896 г. равнялась 19, а в 1909 г. - 22 с вероятной ошибкой для 1896 г. около 2 дней, а для 1909 г. - немного более 1 дня. Эти выводы должны указать на более слабое обращение денег, чем на то указывает большинство вычислений и предположений, которые были сделаны. Мы не должны забывать, однако, что такие люди, как экономисты, которые способны размышлять о денежном обращении, имеют быстрый денежный оборот. Обычно они городские жители и люди сравнительно обеспеченные, каковые, как мы знаем, не держат долго свою наличность бездеятельной. Рабочие, и в особенности бережливые рабочие, которые получают заработную плату помесячно, держат свои деньги на руках в течение нескольких недель, не тратя их. Фермеры и другие обитатели округов с разбросанным населением не тратят своих денег даже по месяцам. По-видимому, скорость обращения денег далеко не одинакова среди различных классов населения и в разных местностях. Теперь мы можем сделать следующее сравнение 1896 и 1909 гг. в отношении денег в обращении, депозитного обращения, скоростей их обращения и общей суммы их обращения, а именно:
Наша дальнейшая задача состоит в интерполировании значений V цля промежутка времени между 1896 и 1909 гг. с соответственными скоростями обращения денег 19 и 22. Результаты приведены в следующей таблице. Вычисления V с 1896 по 1909 г.
§ 5. Вычисления Р и Т для 1896 - 1909 гг. Теперь мы закончили статистический обзор величин М, М', V, V', находящихся в левой части уравнения обмена, и нам остается только рассмотреть две другие величины, Р и Т, находящиеся в правой его части. Сначала мы рассмотрим T. Результаты наших вычислений - в следующей таблице, которая изображает объем торговли (в млрд. долл.) и исчислена согласно ценам 1909 г. Вычисление объема торговли (в млрд. долл. по ценам 1909 г.)
Таблица эта составлена путем приведения к среднему index numbers'ов количеств (но не ценности) торговли в различных отраслях. Цифры, изображающие объем торговли, основаны на данных для 44 видов товаров внутренней торговли, 23 видов импортных товаров и 25 видов экспортных товаров, продажи ценных бумаг, фрахтов железнодорожных перевозок и писем, проходивших через почту. Конечные цифры приспособлены таким образом, чтобы цифра для 1909 г. была равна 399, а именно действительной денежной ценности торговых сделок в этом году, как она получена в другой части уравнения обмена (т. е. MV+M'V'). По отношению друг к другу цифры, изображающие T, независимы от другой части уравнения. Р. Единственный оставшийся нерассмотренным фактор уравнения обмена есть index number цен, т. е. Р. Теоретически его можно вычислить при посредстве других пяти величин этого уравнения, уже вычисленных нами, предполагая, что все наши предыдущие вычисления могут рассчитывать на полную точность. Но возможно, что при вычислении М, М', V и V' могли быть допущены ошибки и таковые, если бы они имели место, были бы повторены в совокупности и в вычислении Р. Следовательно, очень важно проверить такое косвенное вычисление Р непосредственно вычисленными данными. Поступив таким образом, мы будем в состоянии сравнить значения для Р, вычисленные прямым и косвенным путем. Таким же образом при желании мы могли бы сравнить вычисленные косвенным и прямым путем значения М, М', V, V' и Т. Мы ограничимся сравнением двух значений Р, так как именно Р, как мы видели, действительно зависит от пяти других факторов уравнения обмена. Значения Р (включающие цены товаров, ценных бумаг и труда), непосредственно вычисленные в процентах к цифрам 1909 г., принятым за 100, дают следующую таблицу. Index numbers общих цен
Эта таблица основана на цифрах “Bureau of Labor” для оптовых цен. Они немного отличаются от цифр “Bureau of Labor” благодаря тому, что в нашу таблицу включены цены ценных бумаг и заработные платы. Теперь нам остается сравнить эти действительные статистические данные для Р с Р, исчисленным косвенно, из других величин уравнения обмена. Это вычисление и сравнение будут приведены в следующем параграфе. § 6. Р, вычисленное прямо и косвенно Итак, мы вычислили независимо друг от друга все величины уравнения обмена для 14 лет - от 1896 до 1909 г. Но, как уже было установлено, эти шесть величин взаимно связаны уравнением обмена. Возникает вопрос: могут ли вычисленные таким образом величины хотя бы приблизительно осуществить уравнение обмена? Один путь ответа на этот вопрос предложен проф. Kemmerer'ом, а именно он предлагает сравнить статистические данные для каждого отдельного фактора (скажем, для Р), вычисленные непосредственно, как указано выше, со значением этого фактора, вычисленным косвенно, при помощи других пяти величин уравнения обмена. Следующая таблица дает значения Р, полученные этими двумя способами. Index numbers цен, вычисленные
Соответствие между этими двумя рядами цифр более наглядно выражено на рис. 11. 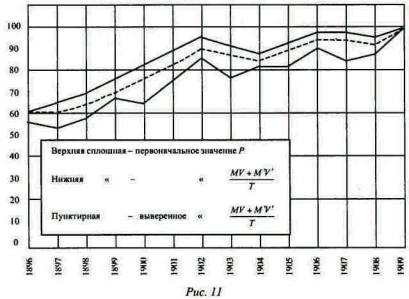 Оба значения, как указывают нижняя и верхняя кривые, совпадают одно с другим замечательно хорошо [Промежуточная кривая на рис. 11 будет объяснена ниже. ]. Точность их соответствия может быть выражена различными путями. Один путь - это сосчитать случаи совпадения и несовпадения в изменении направления или отклонения кривых. Из 12 отклонений в каждой кривой мы имеем 6 случаев совпадения, 3 случая несовпадения и 3 случая нейтральных. Другой способ сравнения был применен проф. Pearson'ом. Этот метод заключается в вычислении величины, которую проф. Pearson называет коэффициентом корреляции. Этот метод указывает на 97% совпадении, что дает преимущество против 23%, найденных проф. Pearson'OM из Дортмута для цифр [См. “Quantity Theory as tested by Kemmerer” // Quarterly Journal of Economics, 1907 - 1908. P. 287. ] проф. Kenunerer'a за 1879 - 1901 гг. Но как уже было указано, коэффициент корреляции для последовательных данных может ввести в заблуждение. Если, как в случае с цифрами проф. Kemmerer'a, коэффициент 0,23 был недостаточным подтверждением параллелизма между его кривыми, то коэффициент 0,97 преувеличивает параллелизм между нашими кривыми. Это преувеличение обычно имеет место тогда, когда обе сравниваемые кривые быстро повышаются или понижаются [Persons исчисляет коэффициент корреляции между цифрами Kemmerer'a для банковских резервов и денег в обращении, включающих банковские резервы, в 0,98, хотя эти две величины не обнаруживают сколько-нибудь значительного соответствия между колебаниями в последовательные годы, но только общее соответствие в том факте, что обе быстро падают. Коэффициент для Р, по исчислениям проф. Kemmerer'a, будет гораздо выше, если вместо того чтобы брать период начиная с 1879 г., который заключает в себе много годов, когда цены значительно изменялись, взять период, начиная с того года, которым начинаем мы, т. е. с 1896-го. Коэффициент корреляции для цифр проф. Kemmerer'a (за 1896 - 1908 гг.) равен 83%; он гораздо выше того, который получен проф. Persons'ом для периода, начинающегося с 1876 г.]. Надлежащим методом применения коэффициента корреляции к последовательным данным является, по-видимому, тот, где этот коэффициент вычисляется не для абсолютных чисел, а для последовательных из года в год отношений этих цифр. Другими словами, мы должны составлять таблицы и сравнивать ежегодно отношения значения Р для каждого года к его значению для предыдущего года и отношение значения (MV+M'V')/T для каждого года к значению (MV+M'V')/T для предыдущего года. Если оба ряда отношений будут повышаться или понижаться одновременно, то кривые будут указывать полный параллелизм или совпадение в последовательных изменениях направления. Фактически результаты этого метода указывают, что коэффициент корреляции равен 57% (или 0,57±0,10, где 0,10 есть величина вероятной ошибки). Цифра 57% есть относительно высокий коэффициент корреляции [Например, никто не будет отрицать, что длина и ширина ореха очень сильно согласованы. Коэффициент их корреляции равен 0,57. Вышина человека и ширина его фигуры коррелируют в размере 35%. ]. Следовательно, мы можем заключить, что “количественная теория” статистически проверена до высокой степени корреляции [Случайно мы можем сравнить здесь относительную степень корреляции цифр проф. Kemmerer'a с нашими цифрами. Для этой цели мы возьмем период 1896 - 1908 гг., который является длиннейшим периодом, общим обоим исследованиям. Для этих годов коэффициент наших цифр равен 54% (или 0,54±0,11) против 37% (или 0,37±0,14) для цифр проф. Kemmerer'a. Эти результаты получены методом исчисления последовательных ежегодных отношений. При методе абсолютных чисел корреляция моих данных равна 95%, а данных проф. Kemmerer'a - 83%. ]. Здесь надо отметить, что только что приведенные коэффициенты корреляции сравнивают уровень цен с тем, каким он был бы согласно статистическому значению пяти величин уравнения обмена, от которых он зависит по так называемой количественной теории. Корреляция была бы меньше, если бы вместо пяти величин была взята только одна. Так, например, коэффициент корреляции для 1896 - 1909 гг. между количеством денег М и ценами Р при методе последовательных из года в год отношений дает 43% (или 0,43±0,13) [При непосредственном (неправильном) сравнении М и Р коэффициент корреляции для 1896 - 1909 гг. будет 97%.]. Но даже и эта цифра является умеренно высокой степенью корреляции. Если противники количественной теории, которые пытаются опровергнуть всякую связь между деньгами и ценами, указывая на отсутствие соответствия между статистическими данными этих двух факторов, подразумевают только, что другие факторы, кроме денег, а именно M', V, V', Т, меняются от времени до времени и что поэтому уровень цен фактически изменяется не в точном параллелизме с количеством денег, то их утверждение является разумным. Но приведенное положение имеет столь же малое,научное значение, как положение, что атмосферное давление не изменяется изо дня в день в точном соотношении с плотностью атмосферы. Мы знаем, что если температура остается неизменной, то давление газа изменяется прямо пропорционально его плотности, но фактически температура редко остается неизменной. Всякий критик, который пытался бы опровергнуть закон Бойля на этом основании, только обнаружил бы свое невежество в понимании действительного значения этого научного закона, а если бы серьезно пытался “опровергнуть его статистическим путем”, вычерчивая ежедневные кривые барометрического давления и плотности атмосферы, он поставил бы себя как ученого в смешное положение. Но если бы кто-нибудь действительно представил себе, что уровень цен зависит исключительно от количества денег, то его, наверно, поправили бы. Но действительно важный вопрос, который изучающие экономику должны понять, это существование закона прямой пропорциональности между количеством денег и уровнем цен, - закона столь же реального, столь же важного и столь же основного в экономической теории денег, насколько закон Бойля о прямой пропорциональности между плотностью и давлением атмосферы является реальным, важным и основным законом в физической теории газов. Я думаю, что частые неудачи в попытках обнаружить существование этого закона обязаны в широкой мере недостатку ясного представления об относящихся сюда величинах. По-видимому, М и Р являются существенными величинами, действительный смысл которых понятен некоторым исследователям. M', V, V' и T редко обсуждаются или даже упоминаются. Но только когда этот вопрос будет поставлен на статистическое основание, в цифрах, измеряющих действительное депозитное обращение, скорости обращения и объем торговли, эти величины будут признаны имеющими реальное существование и значение. Но непредубежденному уму количественная теория в том смысле, в котором мы ее приняли, должна представиться достаточно надежной и без такого рода проверки. Ее лучшим доказательством всегда должно быть априорное, не в том смысле, какой прилагается к доказательству абстрактных математических предложений, но в том смысле, какой прилагается к доказательству закона Бойля. Так, например, известно индуктивным путем, что давление газа в замкнутом пространстве вызывается бомбардированием его молекул в замыкающие его стенки. Равным образом известно индуктивным путем, что давление должно быть пропорционально частоте толчков при предположении, что скорости движения молекул постоянны. Наконец, известно, что частота толчков должна быть пропорциональна количеству молекул, т.е. плотности газа, и что постоянство скорости предполагает постоянство температуры. Из этого следует, что при постоянной температуре давление пропорционально плотности. Таким образом, из результатов, выведенных индуктивным методом, о единичных давлениях молекул, составляющих газ, мы можем вывести дедуктивным путем закон давления газа в целом. Аналогично из индуктивно полученного знания об отдельных случаях обмена, принимая их как бы за молекулы, которые составляют в совокупности обмен в данном обществе, мы можем дедуктивным путем вывести общее уравнение обмена. К счастью, точно так же, как закон Бойля был установлен и дедуктивно и индуктивно, мы можем утверждать теперь, что уравнение обмена было достаточно установлено и дедуктивно и индуктивно. Как раньше было замечено, установление уравнения обмена не является еще в полной мере установлением количественной теории денег, так как уравнение обмена не выясняет, которые из факторов являются причиной, которые следствием. Но на этот вопрос был уже дан ответ в главе VIII. |
