ммвпиэ пз 6 трансформатор Получение целевой функции и решение задачи условной оптимизации. пз 6. Получение целевой функции и решение задачи условной оптимизации
 Скачать 58.02 Kb. Скачать 58.02 Kb.
|
|
Учреждение образования "Белорусский государственный университет информатики и радиоэлектроники" Кафедра проектирования информационно-компьютерных систем Отчёт по практическому занятию №6 на тему «Получение целевой функции и решение задачи условной оптимизации» Проверил: Выполнил: Казючиц В.О. Ст.гр. 913301 Гурин К.А. Минск 2021 Цель работы Получить целевую функцию и решить задачу условной оптимизации на примере силового трансформатора. Общие сведения В качестве целевой функции F рассматривается либо масса М, либо стоимость Ц броневого трансформатора. В качестве оптимизируемых параметров рассматриваются ширина с и высота h окна магнитопровода из электротехнической стали для размещения катушки с обмотками (рис. 1). 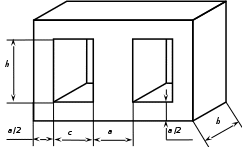 Рисунок 1 – Магнитопровод броневого трансформатора В процессе решения задачи оптимизации требуется получить выражение для целевой функции F(c, h) и найти такие значения размеров с и h, при которых масса М или цена Ц трансформатора минимальна, но площадь окна (произведение с на h) достаточна для размещения обмоток и размер с такой, что обеспечивается необходимый зазор между обмотками и магнитопроводом для обеспечения теплового режима. Решение Исходные данные для задачи оптимизации приведены в таблице 1. Таблица 1 – Исходные данные в соответствии с вариантом
При получении выражений для ограничений учитывается, что ширина окна с должна быть такой, чтобы между обмотками и магнитопроводом оставался зазор Δ не менее 2…3 мм. Общие исходные данные, необходимые для выполнения задачи оптимизации представлены в таблице 2. Таблица 2 – Общие исходные данные
Найдем мощность первичной обмотки: P1 = 1,25 ∙ P2 = 1,25 ∙ 100 = 125 Вт. Силы тока в обмотках: 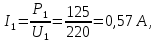 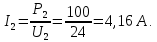 Сечение магнитопровода: Sc = a ∙ b = 25 ∙ 40 = 1000 мм2 = 10 см2. Число витков, приходящиеся на 1В для первичной и вторичной обмоток: 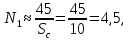 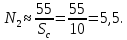 Число витков первичной и вторичной обмоток: ω1 = U1 ∙ N1 = 220 ∙ 4,5 = 990, ω 2 = U2 ∙ N2 = 24 ∙ 5,5 = 132. Плотность тока в первичной и вторичной обмотках: j1 = 0,44 ∙ ln(P1) + 4,8 = 0,44 ∙ ln(125) + 4,8 =6,92 А/мм2, j 2 = 0,44 ∙ ln(P2) + 4,8 = 0,44 ∙ ln(100) + 4,8 = 6,83 А/мм2. Диаметр провода из меди в первичной и вторичной обмотках: 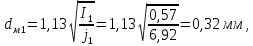 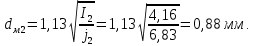 Исходя из полученных размеров провода из меди, диаметр проводов с изоляцией: dиз1 = 0,37 мм, dиз2 = 0,97 мм. Коэффициент разбухания обмотки: kраз1 = [( dиз1 – 0,8 )2 + 2,5]0,064 + 0,03( 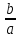 – 1 ) +0,05 = – 1 ) +0,05 == [( 0,37 – 0,8 )2 + 2,5]0,064 + 0,03( 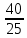 – 1 ) + 0,05 = 1,133 мм, – 1 ) + 0,05 = 1,133 мм,kраз2 = [( dиз2 – 0,8 )2 + 2,5]0,064 + 0,03( 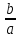 – 1 ) +0,05 = – 1 ) +0,05 == [( 0,97 – 0,8 )2 + 2,5]0,064 + 0,03( 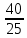 – 1 ) + 0,05 = 1,129 мм. – 1 ) + 0,05 = 1,129 мм.Плотность тока в первичной и вторичной обмотках: hсл = h – 2 ∙ (tк + tз) = h – 2 ∙ (1,5 + 1,5) = h – 6. Число витков первичной и вторичной обмоток: 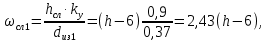 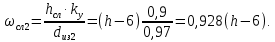 Число слоев в обмотках: 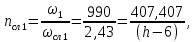 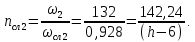 Находим t1 и t2 по формуле: ti = [ 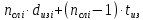 ] ] kразi , kразi ,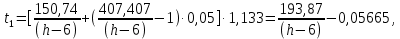 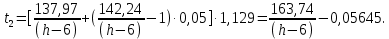 Вычислим среднюю длину витка первичной и вторичной обмоток: 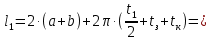 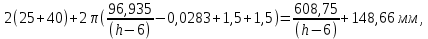 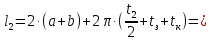 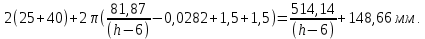 Найдем массы первичной и вторичной обмоток из меди: 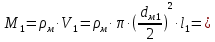 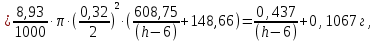 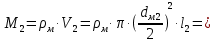 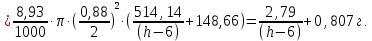 Рассчитаем стоимость меди: 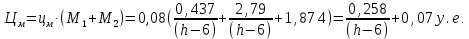 Объем магнитопровода: Vc = (a + 2c + a)  b b (a + h) – 2h (a + h) – 2h c c b = (2 b = (2 25 + 2c) 25 + 2c) 40 40 (25 + h) – 2h (25 + h) – 2h c c 40 = 40 == 2000  (h + c) + 50000 мм3 (h + c) + 50000 мм3Масса стали: 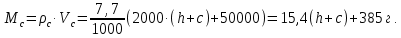 Рассчитаем стоимость стали: 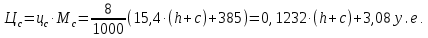 Цена трансформатора складывается из цены обмотки и магнитопровода: Ц = Цс + Цм = 0,123 ∙ (h+c) + 3,08 + 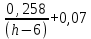 = 0,123 ∙ (h+c) + = 0,123 ∙ (h+c) + 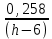 + 3,15 у.е. + 3,15 у.е.Вычислим массу трансформатора: Мтр = М1 + М2 + Мс = 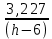 + 15,4(h + c) + 386,874 г. + 15,4(h + c) + 386,874 г.Воспользуемся ограничением, заданным условиями: с – (t1 + t2 + tк + tз) ≤ Δ; Δ = 2…3 мм. Выразим искомую величину c: 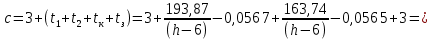 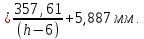 Подставляем найденное значение c в цену трансформатора: 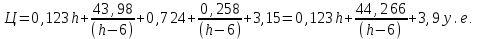 Находим вторую производную полученной функции по параметру h, а также точки экстремума: 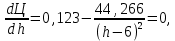 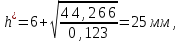 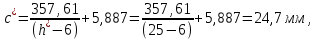 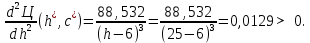 Так как вторая производная 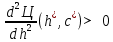 , то функция Ц в найденных точках имеет минимальное значение. Подставив , то функция Ц в найденных точках имеет минимальное значение. Подставив 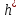 и и 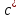 в выражение цены трансформатора, вычислим минимальную цену: в выражение цены трансформатора, вычислим минимальную цену:Ц = 0,123 ∙ (h + c) + 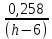 + 3,15 = 0,123 ∙ (25 + 24,7) + + 3,15 = 0,123 ∙ (25 + 24,7) + 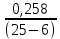 + 3,15 = 9,28 у.е. + 3,15 = 9,28 у.е.Подставляем найденное значение c в массу трансформатора: Мтр = 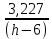 + 15,4(h + c) + 386,87 = + 15,4(h + c) + 386,87 = 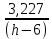 + 15,4(h + + 15,4(h +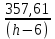 + 5,877) + 386,87 = = 15,4h + + 5,877) + 386,87 = = 15,4h + 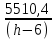 + 477,4 г. + 477,4 г.Находим вторую производную полученной функции по параметру h, а также точки экстремума: 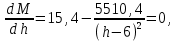 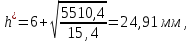 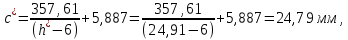 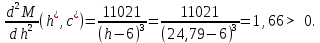 Так как вторая производная 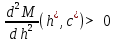 , то функция М в найденных точках имеет минимальное значение. Подставив , то функция М в найденных точках имеет минимальное значение. Подставив 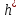 и и 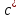 в выражение массы трансформатора, вычислим минимальную массу: в выражение массы трансформатора, вычислим минимальную массу:Мтр 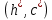 = = 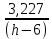 + 15,4(h+c) + 386,9 = + 15,4(h+c) + 386,9 = 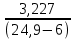 + 15,4(24,9 + 24,8) + 386,9 = = 1152,4 г. + 15,4(24,9 + 24,8) + 386,9 = = 1152,4 г.Вывод В ходе работы получена целевая функция и решена задачу условной оптимизации на примере силового трансформатора. Были найдены значения параметров hи с, соответствующие минимальной цене и массе трансформатора. | ||||||||||||||||||||||||||||||||||||
