Получение периодической последовательности прямоугольных импульсов суммированием гармоник. Построение амплитудного спектра. Ряд Фурье
 Скачать 491.89 Kb. Скачать 491.89 Kb.
|
         Работа №3 «Получение периодической последовательности прямоугольных импульсов суммированием гармоник. Построение амплитудного спектра». Ряд Фурье: 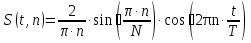
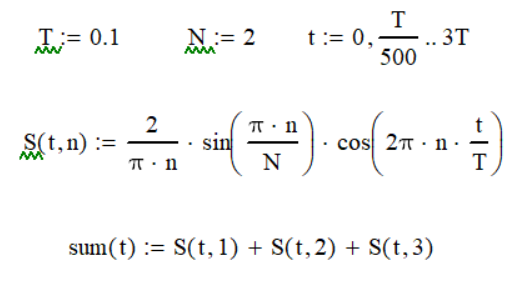 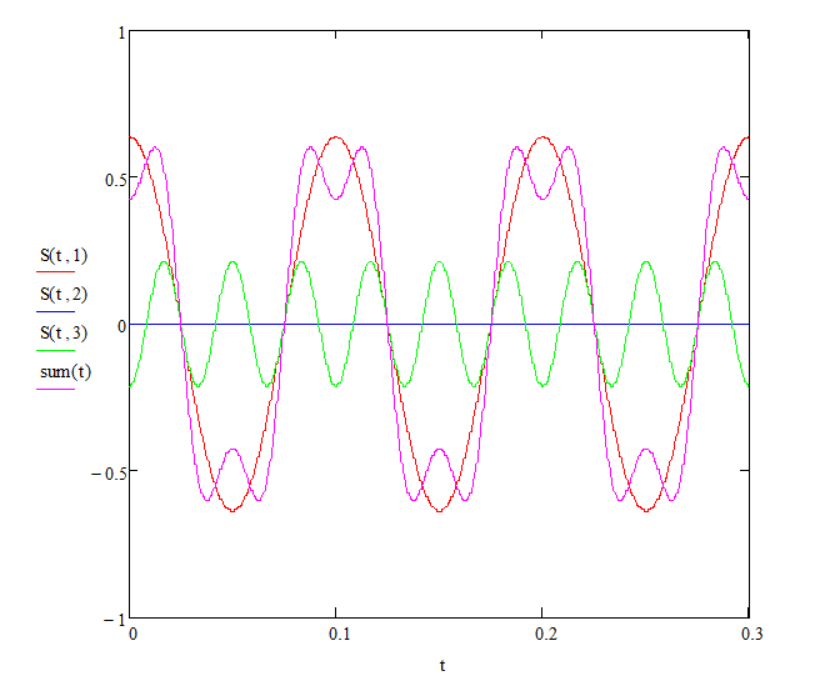 Заметим, что амплитуда второй и четвертой гармоник равна 0. 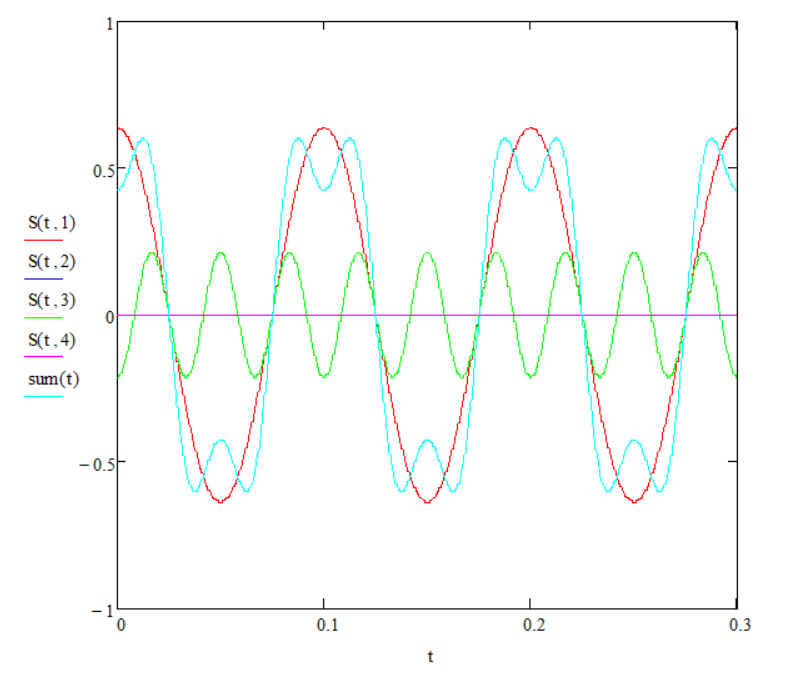 Мы можем сделать вывод, что при скважности 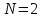 амплитуда всех четных гармоник равна 0. амплитуда всех четных гармоник равна 0.
КОНЕЦ 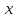 НАЧАЛО 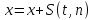 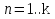 Напишем программу, суммирующую произвольное число гармоник: 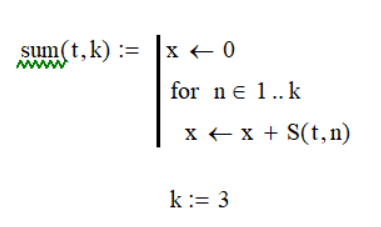 k – количество гармоник.
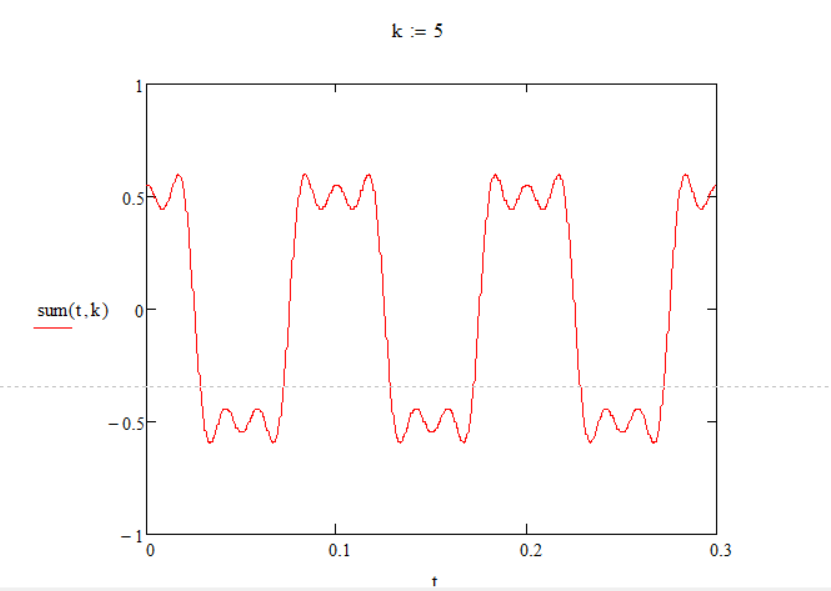 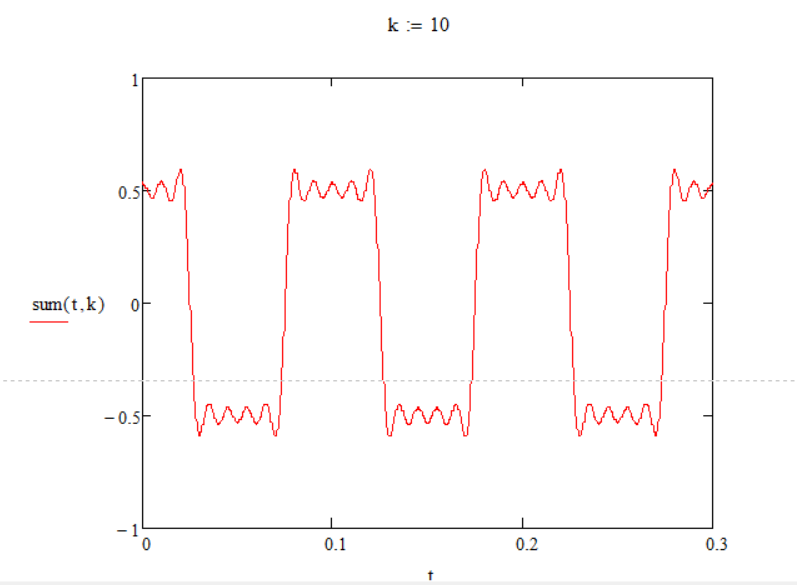 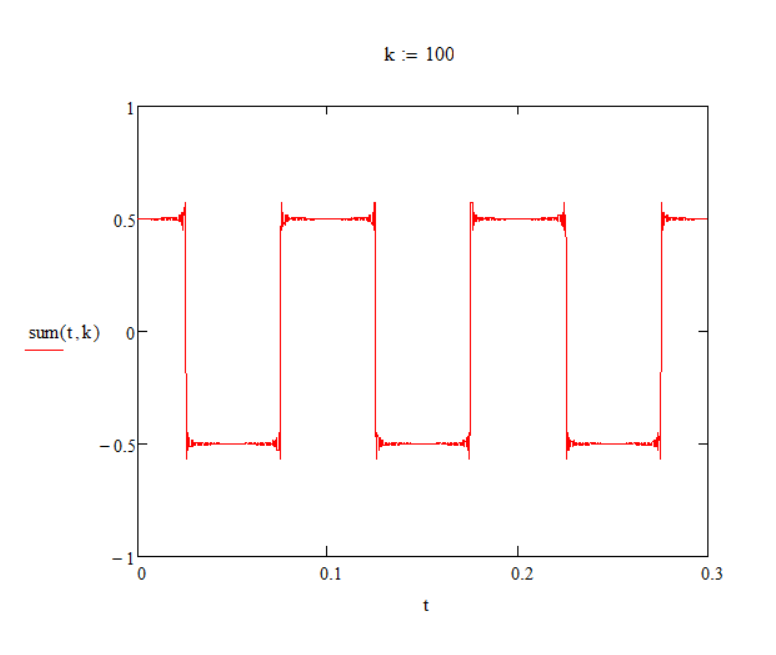 По графикам, изображённым выше можно понять, что последовательность из прямоугольных импульсов можно получить при помощи суммирования синусоид со всё более высокими частотами и всё более малыми амплитудами. И степень” прямоугольности” будет зависеть от количества суммируемых синусоид.
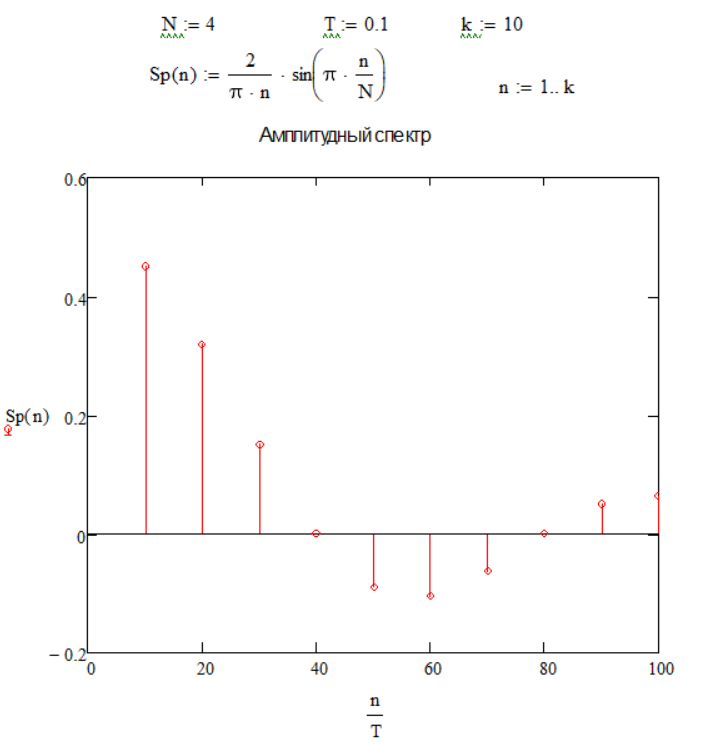
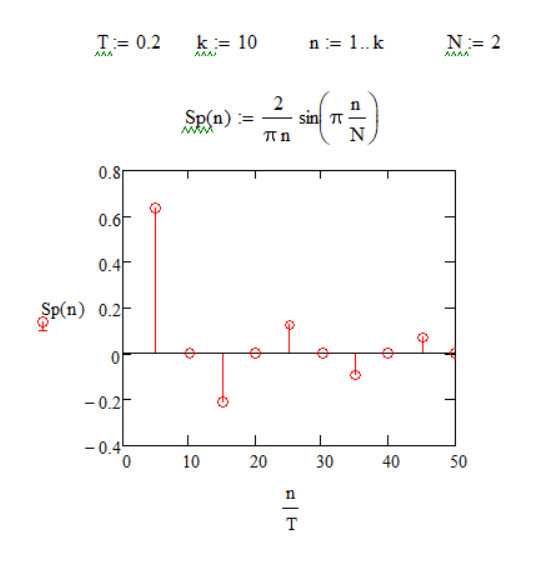 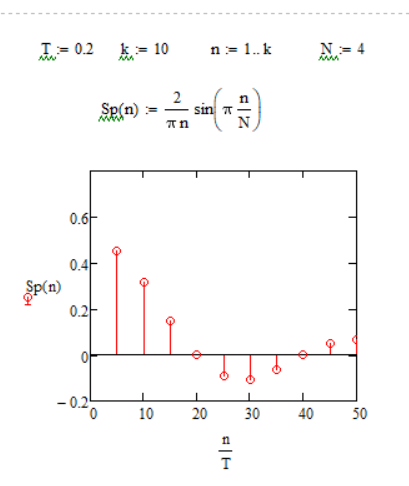 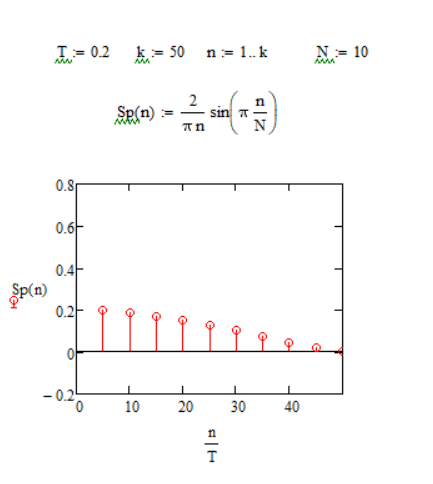 Из графиков можно сделать вывод, что при увеличении скважности уменьшаются амплитуды гармоник, спектральные линии становятся гуще. Количество гармоник в лепестке равно скважности.
 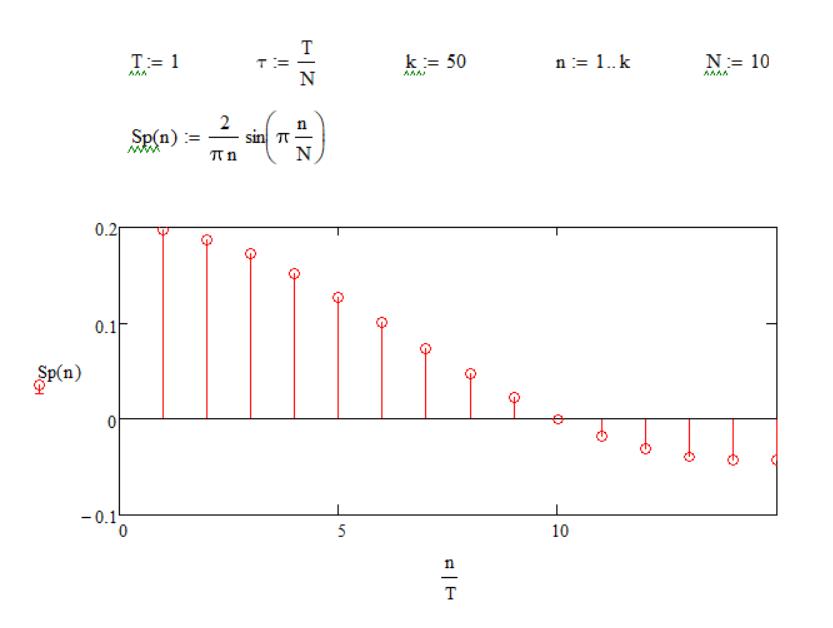  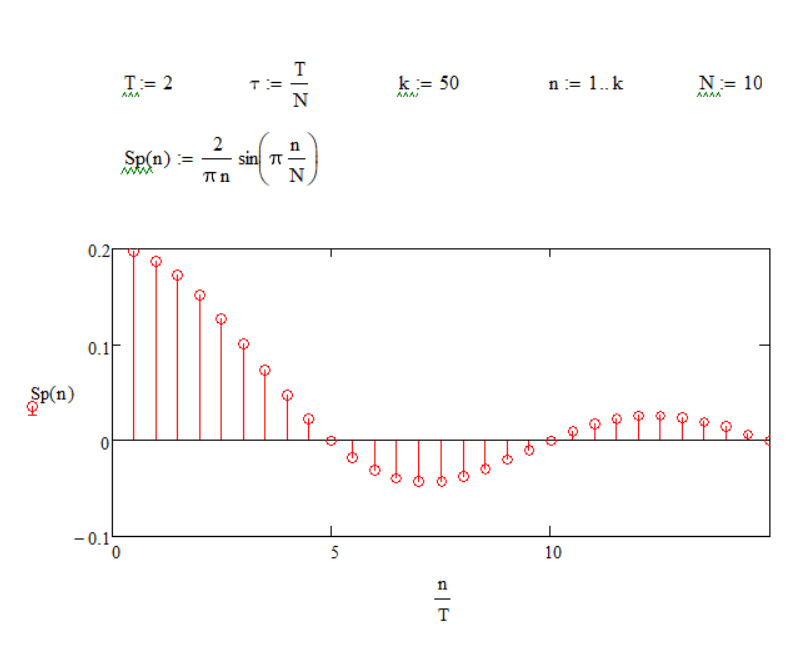 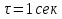 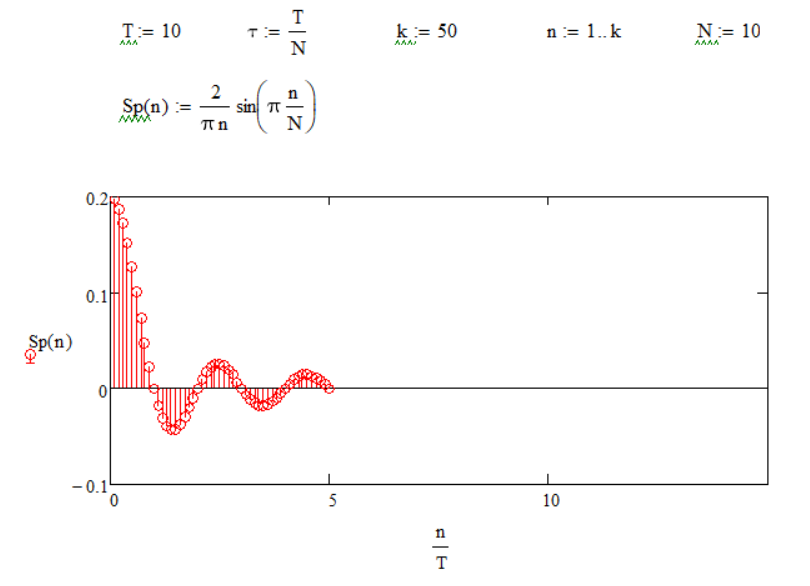 По этим графикам можно сделать вывод, что ширина лепестка обратно пропорциональна длительности импульса. Вывод: Значение скважности N = i говорит нам о том, что амплитуда каждой i - ой гармоники равна 0 (Например: при N = 3, амплитуда каждой третьей гармоники равна 0). В спектре непериодического сигнала вместо отдельных гармоник бесконечно большое число синусоидальных колебаний с бесконечно близкими частотами, заполняющими всю шкалу частот. Причем амплитуда при таких колебаниях постоянно уменьшая и становится исчезающе малой. |

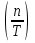 , длина которых равна амплитуде соответствующей гармоники:
, длина которых равна амплитуде соответствующей гармоники: 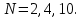
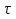 = 0.1, 0.2, 1 сек. Сделать выводы.
= 0.1, 0.2, 1 сек. Сделать выводы.